放物線 (数学): 定義、方程式、要素、例など…

このページでは、放物線とは何なのか、何を表しているのか、その要素 (焦点、準線、頂点など)、方程式 (放物線のさまざまなタイプの方程式)、例、解答済みの演習など、放物線に関するすべての情報を見つけることができます。その特性、用途など…

たとえ話とは何ですか？

放物線は非常に異なる意味を持つ概念ですが、その数学的定義は次のとおりです。

数学では、放物線は、固定点 (焦点と呼ばれる) と固定線 (準線と呼ばれる) から等距離にある平面上の点の軌跡です。

したがって、放物線内のどの点も、その焦点および準線からの距離は同じになります。

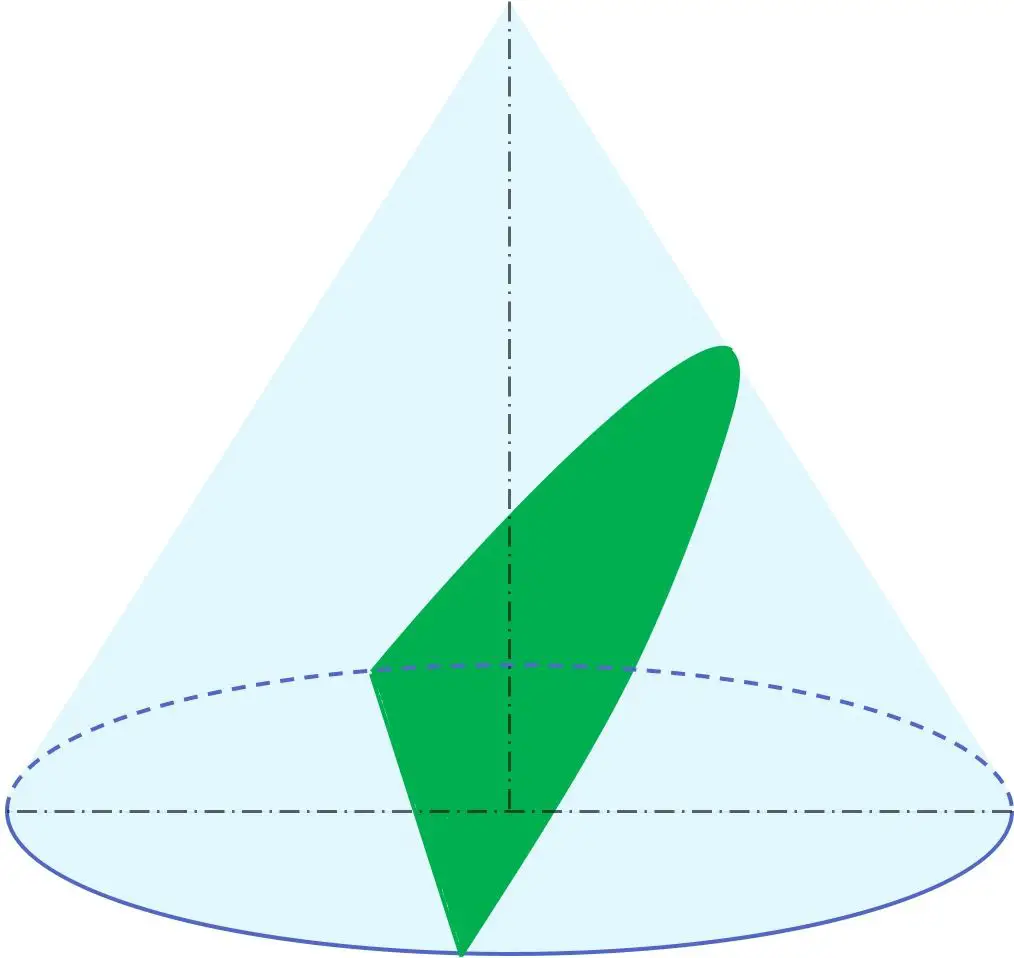
さらに、幾何学では、放物線は、円周、楕円、双曲線と並ぶ円錐曲線の 1 つです。つまり、円錐から放物線が得られます。

特に、放物線は、円錐の母線の角度と等しい回転軸に対する傾斜角を有する平面による円錐の断面から得られる。したがって、放物線を含む平面は円錐の母線と平行になります。

放物線の要素

放物線の特性は、次の要素によって決まります。

焦点 (F) : 放物線内の固定点です。放物線の任意の点から焦点までの距離は、この同じ点から放物線の準点までの距離に等しい。
Directrix (D) : 放物線の外側の固定線です。放物線の点は、準線から放物線の焦点までと同じ距離にあります。
パラメータ (p) : 焦点からディレクターまでの距離です。
半径ベクトル (R) : 放物線の点と焦点を結ぶ線分です。その値は、点から準線までの距離と一致します。
軸 (E) : 焦点を通過する準線に垂直な線であり、放物線の対称軸です。下のグラフでは、コンピューターの軸 (Y 軸) に対応します。焦点軸とも呼ばれます。
頂点 (V) : 放物線とその軸との交点です。
焦点距離: 焦点と頂点の間、または準線と頂点の間の距離です。その値は常に次と等しくなります。
$\displaystyle \frac{p}{2}.$

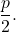
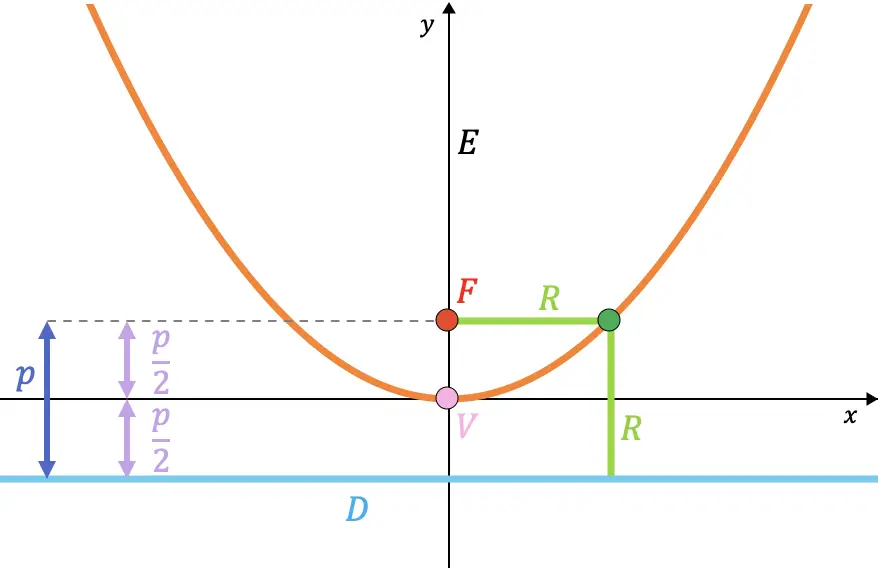
右側

放物線の右側は、焦点を通過し、準線に平行な放物線の内側の弦です。

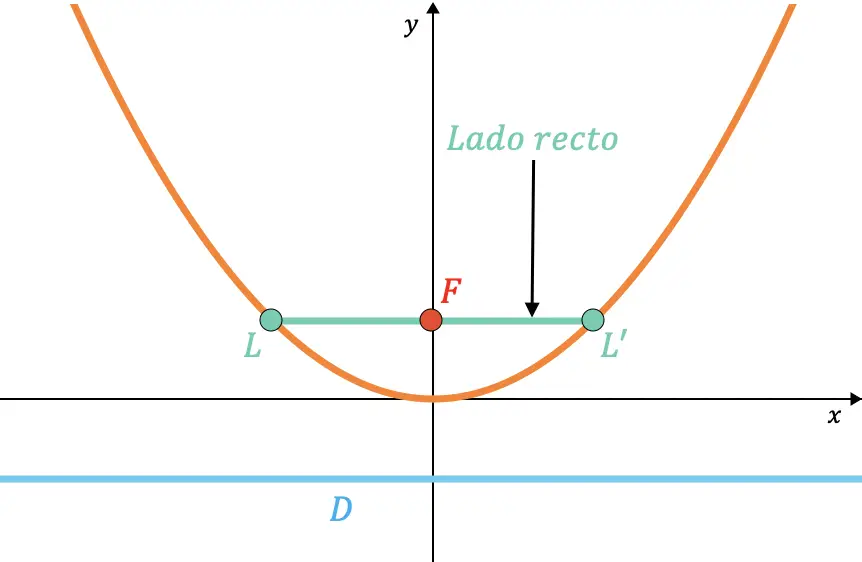
同様に、右辺の長さは常にパラメータの値の 2 倍であることがわかります。

$p.$

$\lvert LL'\rvert = 2p$

一方、右側の端を通る放物線の接線2本は、右側と45度の角度をなし、放物線の頂点で交わります。

放物線方程式

放物線の方程式は、常に少なくとも 1 つの二乗項を持たなければならないため、二次関数の一種です。さらに、放物線の方程式は、その水平方向または垂直方向によって異なります。

したがって、解析幾何学では、放物線を数学的に表現する方法がいくつかあります。正準方程式または縮小方程式、常方程式、および放物線の一般方程式です。

放物線の縮小方程式または正準方程式

縮小方程式または正準方程式が他の放物線方程式と異なるのは、放物線の頂点が座標の原点、つまり点 (0,0) であることです。

放物線の縮小方程式の形式は、それが水平か垂直かによって異なります。考えられる 4 つのバリエーションが示されている次の図を見てください。

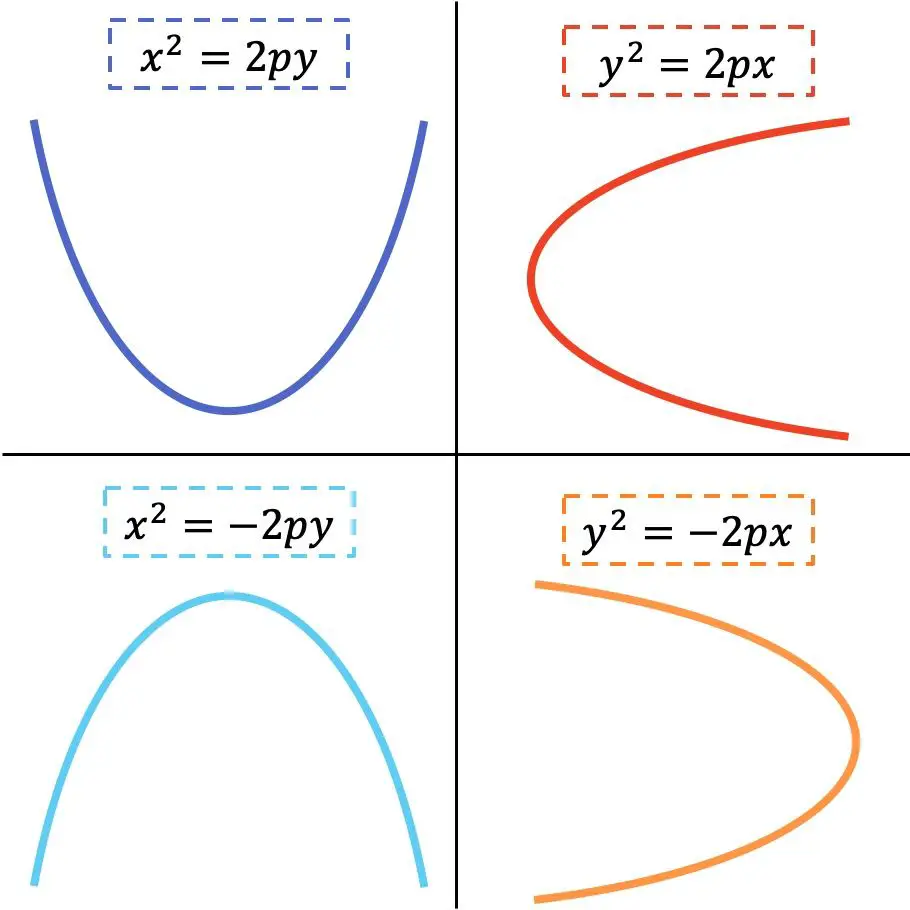
金

$p$

は放物線の特性パラメータです。

前の画像からわかるように、変数xが 2 乗されると放物線は垂直になり、一方、変数yが 2 乗されると放物線は水平になります。一方、放物線の枝の方向は方程式の符号に依存します。

放物線の常方程式

放物線の頂点または中心が座標の原点 (縮小方程式または正準方程式) に対応する場合、放物線の方程式がどのようになるかを見てきましたが、頂点が「原点」の外側にある場合、放物線の方程式はどうなるでしょうか?

放物線の頂点が任意の点である場合、放物線の常方程式を使用します。その式は次のとおりです。

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}}(x-x_0 )^2 = 2p (y-y_0) \quad}$

放物線の中心または頂点が点となる場所

$V(x_0,y_0).$

前の式は垂直方向の放物線に対応します。つまり、放物線の焦点軸は Y 軸に平行です。

同様に、水平方向の放物線 (焦点軸が X 軸に平行) を定義するには、放物線の常方程式の次の変形を使用する必要があります。

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} (y-y_0 )^2 = 2p (x-x_0)\quad}$

前と同様に、放物線の中心または頂点が点になります。

$V(x_0,y_0).$

放物線の一般方程式

これまでに解析したすべての放物線方程式は、水平または垂直の放物線を表現するために使用されます。しかし明らかに、放物線は斜めになったり傾斜したりすることもあります。

さて、このタイプの放物線を表現するには、一般的な放物線の方程式を使用します。その公式は次のとおりです。

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} Ax^2 + Bxy+Cy^2 +Dx+Ey + F = 0 \quad}$

上の式は、係数が次の場合にのみ放物線になります。

$A$

そして

$C$

同時にゼロではなく、さらに次の条件が満たされます。

$B^2-4AC =0$

方程式から放物線の頂点、焦点、準線を見つける方法の例

多くの放物線の演習や問題では、特定の放物線の頂点、焦点、準線を計算するように求められます。したがって、例を通してこれがどのように行われるかを見てみましょう。

次の放物線の頂点、焦点、準線を見つけます。

$x^2 = 4y$

このタイプの放物線問題を解決するための基本的なことは、放物線のパラメーターpを決定することです。この場合、放物線の方程式は、縮小方程式または正準方程式 (垂直放物線) に対応します。

$x^2 = 2py$

したがって、パラメータp は次のようになります。

$2p = 4$

$p = \cfrac{4}{2}$

$p = 2$

一方、放物線は縮小方程式または正準方程式に従うため、その頂点または中心が座標の原点にあることを意味します。

$\bm{V(0,0)}$

放物線の頂点とパラメータ値がわかれば、その焦点と準線を簡単に見つけることができます。

方程式の二次項は変数xであるため、放物線の軸は OY 軸に平行になります。実際、その頂点は点 (0,0) であるため、放物線の軸は OY になります。軸そのもの。この場合、放物線の焦点は常に放物線の軸上にあり、距離はです。

$p/2$

放物線の頂点からの座標なので、次のとおりです。

$\displaystyle F\left(0, \frac{p}{2} \right)$

$\displaystyle F\left(0, \frac{2}{2} \right)$

$\displaystyle \bm{F\left(0,1 \right)}$

同様に、ガイドラインは離れたところにある水平線になります。

$p/2$

座標の原点である放物線の頂点から。したがって、直線の方程式は次のようになります。

$y=-\cfrac{p}{2}$

$y=-\cfrac{2}{2}$

$\bm{y=-1}}$

放物線は以下にグラフ化されているので、結果を確認できます。

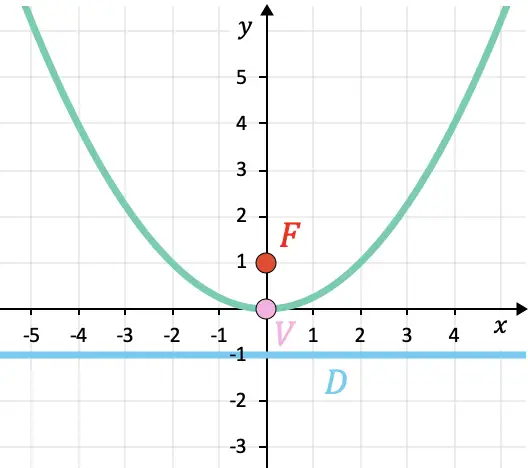
放物線の性質

すべての放物線には次の特性があります。

放物線は開いた曲線、つまり、無制限に伸びる共通点のない 2 つの枝で構成されています。
各放物線は、その放物線の頂点が位置する固有の対称軸を持っています。
垂直方向の放物線は枝が上に行くと凸になります。逆に、枝が下がると放物線は凹面になります。
放物線の離心率は 1 (1) に相当します。離心率は、この場合、焦点から放物線の中心までの距離を頂点から準線までの距離で割ることによって計算される係数です (2 つの距離の値は常に一致します)。
前の特性から、すべての放物線は類似または類似していることがわかります。
放物線には漸近線がありません。

放物線状のアプリケーション

たとえ話の意味をよく理解したところで、「たとえ話の意味は何だろう？」と疑問に思っているかもしれません。

そうですね、あなたにはそうは思えないかもしれませんが、放物線の幾何学的形状は実生活では非常に一般的です。たとえば、特にバスケットボールでは、ボールを投げるときに放物線運動をすることがよくあります。放物線方程式は、ボールがたどる放物線の軌道を分析的に研究するのに非常に役立ちます。

このパラボラアンテナのもう 1 つの用途はアンテナに関するものです (そのため、パラボラアンテナという名前が付けられています)。対称軸に平行なパラボラ形状の物体に当たる各光線は焦点に向かって直接反射されるため、つまり、パラボラアンテナに向かうすべての光線は焦点に集中し、これをさまざまな方法で使用できます。これが、たとえ話の焦点が非常に重要である理由です。