指数関数: 特性、グラフ表現、演習など

このページでは、指数関数とは何か、また指数関数をグラフ上で表現する方法について説明します。さらに、そのすべての特徴といくつかの例を見て、それを完全に理解します。最後に、指数関数に関する演習と問題を段階的に解いて練習することができます。

指数関数とは何ですか?

指数関数の定義は次のとおりです。

数学では、指数関数は、べき乗の指数に独立変数xを持つ関数です。つまり、次のとおりです。

$f(x)=a^x$

金

$a$

は正の実数であり、1 とは異なります。

指数関数の例

次の関数は指数関数の例です。

$f(x)=3^{x}$

$f(x)=4^{-x}$

$\displaystyle f(x)=\left( \frac{1}{2} \right)^x$

$f(x)=5^x$

指数関数の特徴

指数関数には次の特性があります。

指数関数の定義域は実数で構成されます。つまり、指数関数はxの任意の値に対して存在します。

$\text{Dom } f=\mathbff{R}$

ただし、この関数は正の値のみを取るため、指数関数の範囲は正の実数で構成されます。

$\text{Im } f= (0,+\infty)$

すべての指数関数は連続関数でもあり、単射関数でもあります。

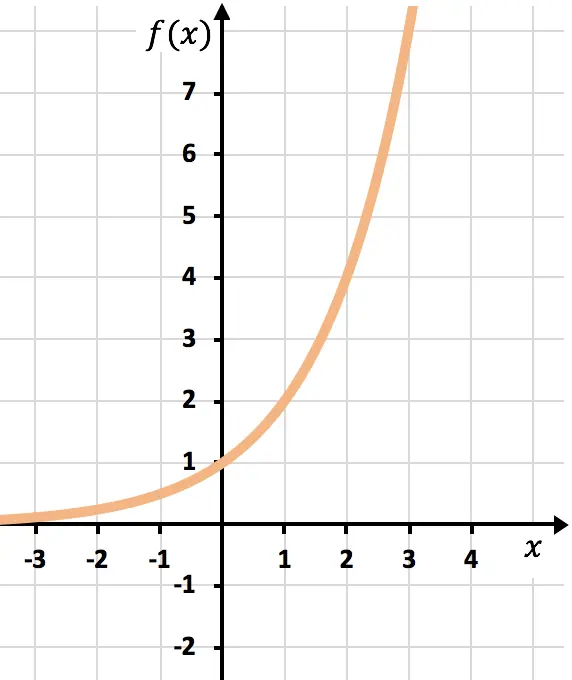
関数が変換されない場合、指数関数は点 (0,1) を通過します。ゼロと評価される関数は常に 1 を返すためです。

$f(0)=a^0=1$

同様に、x=1 における指数関数の値は底と等しくなります。

$f(1)=a^1=a$

パワーベースなら
$(a)$

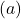
が 1 より大きい場合、指数関数は増加します。一方、係数が

$a$

が 0 と 1 の間の範囲にある場合、指数関数は減少します。

一般に、X 軸は指数関数の水平漸近線です。

指数関数の逆関数が対数関数です。したがって、指数関数と対数関数のグラフは、底が同じであれば、線 y=x に関して対称になります。

指数関数をグラフ化する方法

指数関数は非常に簡単に表現できます。それでは、例を使用してグラフ上に指数関数をグラフ化する方法を見てみましょう。

次の指数関数をグラフにプロットします。

$f(x)=2^x$

指数関数では、常にすべて実数になるため、定義域を計算する必要はありません。

$\text{Dom } f = \mathbb{R}$

したがって、値の表を作成するだけで十分です。このような関数は点ごとに大きく変化するため、5 つの点を計算します。しかし、計算するポイントが増えるほど、関数の表現はより正確になります。

$x= 0 \ \longrightarrow \ f(0)=2^0= 1$

$x= 1 \ \longrightarrow \ f(1)=2^1= 2$

$x= 2 \ \longrightarrow \ f(2)=2^2= 4$

$x= -1 \ \longrightarrow \ f(-1)=2^{-1}= 0,5$

$x= -2 \ \longrightarrow \ f(-2)=2^{-2}= 0,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 4 \\ -1 & 0,5 \\ -2 & 0,25 \end{array}$

値の表内の点を見つけるには、手動で計算するのが複雑であるため、電卓を使用することをお勧めします。

ここで、グラフ上の点を表します。

最後に、点を結合して関数を拡張します。

右側の関数は無限大まで増大し続けることに注意してください。

対照的に、左側の関数は減少しますが、0 には決して達しません。0 に非常に近づいても、決して触れません。これは、線 y=0 (x 軸) が水平漸近線であることを意味します。

指数関数に関する演習を解決しました

演習 1

次の指数関数をグラフにします。

$f(x)= 2^x+1$

解決策を見る

これは指数関数であるため、それを表すには、変数 x に値を与える値のテーブルを作成する必要があります。

$x= 0 \ \longrightarrow \ f(0)= 2^0+1=2$

$x= 1 \ \longrightarrow \ f(1)= 2^1+1=3$

$x= 2 \ \longrightarrow \ f(2)= 2^2+1=5$

$x= -1 \ \longrightarrow \ f(-1)= 2^{-1}+1=1,5$

$x= -2 \ \longrightarrow \ f(-2)= 2^{-2}+1=1,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ 2 & 5 \\ -1 & 1,5 \\ -2 & 1,25 \end{array}$

値の表を取得したら、得られた点をグラフ上にプロットし、関数をプロットします。

右側の関数は無限大まで増大し続けることに注意してください。一方、左側では、関数は減少しますが、1 を超えることはありません。実際、関数は右側に水平漸近線 y=1 を持っています。

この場合、関数に向かって上向きに 1 単位の垂直移動が行われたため、水平漸近線は OX 軸ではなく y=1 にあります。

演習 2

次の指数関数をグラフにプロットします。

$\displaystyle f(x)= \left(\frac{1}{3}\right)^x$

解決策を見る

これは指数関数であるため、グラフで表すには、変数 x に値を与える値のテーブルを作成する必要があります。

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{3}\right)^0 = 1$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{3}\right)^1 = 0,33$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{3}\right)^2 = 0,11$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{3}\right)^{-1} = 3$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{3}\right)^{-2} = 9$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 0,33 \\ 2 & 0,11 \\ -1 & 3 \\ -2 & 9 \end{array}$

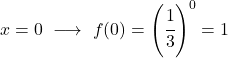
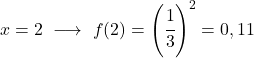
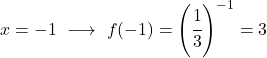
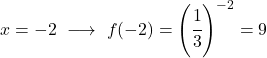
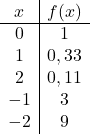
値の表を取得したら、計算された点をグラフ上にプロットし、関数を描画します。

左側の関数は無限大まで増加し続けることに注意してください。一方、右側では、関数は減少しますが、0 を超えることはありません。実際、関数は y=0 (X 軸) で水平方向の漸近線を持ちます。

演習 3

次の指数関数をグラフにプロットします。

$\displaystyle f(x)= \left(\frac{1}{2}\right)^x+3$

解決策を見る

これは指数関数であるため、それを描画するには、いくつかの点で関数を評価する値のテーブルを作成する必要があります。

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{2}\right)^0+3 = 4$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{2}\right)^1+3 = 3,5$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{2}\right)^2+3 = 3,25$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{2}\right)^{-1}+3 = 5$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{2}\right)^{-2}+3 = 7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 4 \\ 1 & 3,5 \\ 2 & 3,25 \\ -1 & 5 \\ -2 & 7 \end{array}$

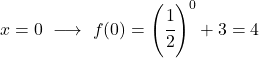
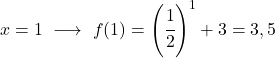
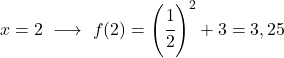
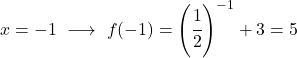
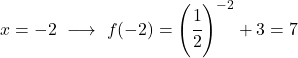
最後に、取得した点をグラフ上に表し、関数をプロットします。

左側の関数は無限にまで無制限に増加することに注意してください。一方、右側では、関数は減少しますが、3 を超えることはありません。実際、この関数は y=3 で水平方向の漸近線を持っています。

この場合、関数が垂直方向に 3 単位上に移動されているため、水平方向の漸近線は X 軸ではなく y=3 にあります。

演習 4

指数関数に関する次の問題を解きなさい。

の値を決定します
$k$

次の指数関数が点 (2.8) を通過するようにします。

$f(x)=k\cdot 2^x$

解決策を見る

関数は点 (2,8) を通過する必要があるため、点のxとf(x)の値を関数に代入して定数k の値を見つけることができます。

$f(x)=k\cdot 2^x \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 8} \ 8 = k \cdot 2^2$

そして、結果として得られた方程式を解きます。

$8 = k \cdot 2^2$

$8 = k \cdot 4$

$\cfrac{8}{4} = k$

$\bm{ 2 = k}$

演習 5

指数関数に関する次の問題を解きなさい。

シロアリの集団は次の関数に従って繁殖します。

$f(t)=3^{t+1}$

金

$f(t)$

はシロアリの数であり、

$t$

何か月も経ちました。

1年後には何匹のシロアリがいるでしょうか？

解決策を見る

1 年間に発生するシロアリの数を計算するには、関数に経過時間 (1 年) を代入するだけです。ただし、関数tは年ではなく経過月であるため、1 年は 12 か月であるため、 t =12 と置く必要があります。

$f(t)=3^{t+1}$

$f(12)=3^{12+1}$

$f(12)=3^{13}$

電卓を使って解きます。

$f(12)= 1594323$

つまり、1年後には1,594,323匹のシロアリが存在することになります。

指数関数とは何ですか?

指数関数の例

指数関数の特徴

指数関数をグラフ化する方法

指数関数に関する演習を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする 返信をキャンセル

コメントする返信をキャンセル