ここでは、あらゆる種類の注目すべきアイデンティティ (または注目すべき製品) の解決方法について説明します。すべての注目すべきアイデンティティの公式が何であるか、また、段階的に解決される例と演習を確認することができます。さらに、これらの有名な数学的法則が何に使われるのかについても説明します。
👉👉 以下では、各注目すべきアイデンティティをステップごとに説明しますが、必要に応じて、すべての式がまとめられている表 😉に直接移動することもできます。 👈👈
注目すべきアイデンティティ (または注目すべき製品) とは何ですか?
顕著な恒等式は、顕著な積または顕著な等式とも呼ばれ、多項式の演算を直接解くことを可能にする数学的規則です。
最も一般的な注目すべき恒等式は、和の 2 乗、差の 2 乗 (または減算)、および和と差の積です。

ただし、以下では、これらの注目すべき製品の計算方法を説明するだけでなく、存在する注目すべきアイデンティティのすべての種類も示します。
注目すべき恒等式(または製品)
注目すべき製品 (または注目すべき同等性) の定義を理解したら、注目すべきアイデンティティの公式が何であるかがわかります。一方、フォーミュラのデモに興味がある場合は、「デモを表示」ボタンをクリックしてフォーミュラを表示できます。
和の二乗
和の 2 乗、または二乗和は、主要な注目すべき恒等式の 1 つです。より正確には、これは 2 つの正の項の 2 乗を含む二項式です。つまり、その代数表現は(a+b) 2です。
したがって、和の二乗の公式は次のようになります。

2 に累乗した正の二項式から始めると:
![]()
数学的には、上の平方は因数に相当します。
![]()
それ自体を乗算します:
![]()
したがって、分布特性を使用して多項式を乗算します。
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
得られた 4 つの項のうち、
![]()
そして
![]()
似ているのでグループ化できます。
![]()
ここまでで、二乗和を導出する式の式にすでに到達しました。
![]()
興味深いことに、この種の注目すべき製品の表現の開発は完全二乗三項式と呼ばれます。
したがって、和の 2 乗は、最初の項の 2 乗に、最初の項と 2 番目の項の積の 2 倍を加え、2 番目の項の 2 乗を加えたものに等しくなります。
したがって、二乗和を解くには、それぞれの加算値を両方に加算するだけでは不十分ですが、さらに、2 つの加算値を互いに乗算して 2 を乗算する必要があります。このタイプの非常に典型的なエラーであるため、これを覚えておくことが重要です。製品のこの用語を忘れることは顕著です。

例:
- 対応する式を適用して、次の注目すべきアイデンティティを計算します。
![]()
これまで見てきたように、二乗和の注目すべき等価性を表す公式は次のとおりです。
![]()
したがって、最初にパラメータを特定する必要があります
![]()
そして
![]()
式の。この場合、
![]()
を表します
![]()
ペアと
![]()
番号 5 に対応します。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
さて、次の値がわかったところで、
![]()
そしての
![]()
正の二乗二項式の公式を使用して結果を求めることができます。

差の二乗
差の 2 乗、または差の 2 乗は、最もよく使用される 3 つの有名な恒等式のもう 1 つです。特に、これは、正の項と 2 に累乗された別の負の項によって形成される二項式に対応します。つまり、その代数式は(ab) 2です。
したがって、差の 2 乗 (または減算の 2 乗) の式は次のとおりです。

二乗減算の二項式から:
![]()
明らかに、前の累乗は係数の積に等しい
![]()
それ自体を乗算します:
![]()
次に、分配プロパティを適用して 2 つの括弧を乗算します。
![Rendered by QuickLaTeX.com \begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b46073fd758d93fff8956f0a8dd57af_l3.png)
したがって、式の確認を完了するには、類似した用語をグループ化するだけです。
![]()
次に、差の二乗の公式が数学的に証明されます。
![]()
したがって、差の 2 乗は、最初の項の 2 乗から、最初の項と 2 番目の項の積の 2 倍を引いたものに、2 番目の項の 2 乗を加えたものと等しくなります。
二乗和の顕著な等価性に関しては、次の方程式が間違っているため、式の中項を忘れずに置く必要があります。

例:
- 次の二乗差の注目すべき等式を解きます。
![]()
これは二乗減算の注目すべき積であるため、対応する式を適用する必要があります。
![]()
次に、未知数の値が何であるかを特定する必要があります。
![]()
そして
![]()
式の。この場合、
![]()
変数です
![]()
そして
![]()
番号 3 に対応します。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1bb2d14a30d2cdabae6458f5df32392a_l3.png)
負号はパラメータの一部ではないことに注意してください。
![]()
ただし、この式を正しく適用するには、常に符号なしの数値を使用する必要があります。
したがって、私たちはすでに次の値を知っています
![]()
そしての
![]()
したがって、注目すべきアイデンティティを解決するには、これらの値を式に代入するだけで十分です。

差による合計
和と差の積は、最もよく使用される 3 つの注目すべきアイデンティティの 1 つです。その名前が示すように、これは正の二項式に共役二項式を乗算したものです (同じ二項式ですが、中間の符号が変更されています)。つまり、このタイプの注目すべき積の代数表現は(a +b) · (ab)です。 。
和と差の積の顕著な恒等式は次のとおりです。

任意の 2 つの項の減算による合計の積から開始します。
![]()
式を実証するには、分配プロパティを使用して最初のかっこと 2 番目のかっこを掛けるだけです。
![Rendered by QuickLaTeX.com \begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-346d3d7ca4da1e71fad52c84a33ef4fc_l3.png)
次に、類似した用語をグループ化します。
![]()
こうして私たちは驚くべき平等の表現を達成しました。したがって、この注目すべきタイプのアイデンティティの公式は次のように証明されます。
![]()
したがって、2 つの量の差と合計の積は、これらの量の 2 乗の差に等しくなります。言い換えると、2 つの異なる項の合計に同じ 2 つの項を減算することは、2 つの項をそれぞれ 2 乗して減算することと同じです。
例:
- 対応する式を使用して、2 つの異なる項の差による合計の次の注目すべき積を求めます。
![]()
上で見たように、和と差を乗算する注目すべき等価性を表す式は次のとおりです。
![]()
まず最初に、文字の値を特定する必要があります。
![]()
そして
![]()
式の。この場合
![]()
変数に対応する
![]()
そして
![]()
番号2に相当します。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-87b76b09924467ba75f033336e6a18e5_l3.png)
そして、パラメーターがどのような値を取るかをすでに知っている場合
![]()
そして
![]()
合計と差の積に次の式を適用します。
三項の二乗
三項式 (3 つの項で構成される多項式) の2 乗は、第 1 項の 2 乗、第 2 項の 2 乗、第 3 項の 2 乗、第 1 項の 2 倍に第 2 項を加え、第 1 項の 2 倍を加えたものに等しくなります。 3 番目までに、2 番目の 2 倍を加えて 3 番目になります。

任意の 3 項の 2 乗から:
![]()
上の平方は、それ自体を乗算した三項式に因数分解できます。
![]()
ここで多項式の乗算を解きます。
![]()
最後に、類似した用語をグループ化します。
![]()
このようにして、すでに式の表現に到達しているため、三項式の二乗の公式が示されます。
![]()
例:
- 次の注目すべき等式を見つけます。
![]()
三項式の二乗の公式は次のとおりです。
![]()
すべての注目すべき等式と同様に、最初に式内の未知数の値を特定する必要があります。この演習では
![]()
東
![]()
係数
![]()
に対応する
![]()
そして
![]()
は独立項 3 です。
![Rendered by QuickLaTeX.com \left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55e06f44486e75e9153a60d36e83bc37_l3.png)
すでに値がわかっている場合は、これらの値を式に代入して計算を行うだけです。

注目すべきアイデンティティ (または製品) の 3 乗
すべての注目すべきアイデンティティの 2 乗、つまり 2 のべき乗によって形成されるすべてのタイプの注目すべきアイデンティティを研究しました。 さて、これからは注目すべきアイデンティティの 3 乗を分析します。もちろん、3 乗恒等式はもう少し複雑ですが、非常に便利でもあります。
和の立方体
和の注目すべき立方積は、 2 つの要素が正である 3 乗の二項式 (2 つの単項式のみを含む多項式) です。したがって、代数的には、和の 3 乗は(a+b) 3と表されます。
和の 3 乗の注目すべき等価性を表す公式は次のとおりです。

正の二項三乗から始める:
![]()
上記のべき乗は、係数の積に因数分解できます。
![]()
その正方形によって:
![]()
同様に、注目すべき二乗等式で見たように、二項
![]()
これは和の二乗の公式で解くことができます。
![]()
次に、2 つの多項式を掛け合わせます。
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-06771ecbb13542eae2a68477f849d729_l3.png)
最後に、類似した用語をグループ化するだけです。
![]()
したがって、二項和の 3 乗の注目すべき恒等式が検証されます。
![]()
つまり、合計を 3 に累乗すると、最初の値の 3 乗に 2 番目の値の 2 乗の 3 倍を加え、1 番目の値の 2 乗の 3 倍と 2 番目の値の 3 乗を加えたものに等しくなります。
例:
- 対応する公式を使用して、次の 3 乗和の注目すべき恒等式を解きます。
![]()
この問題では、2 つの項が正である 3 乗の二項式があります。したがって、3 乗和を求める公式を使用する必要があります。
![]()
次に、パラメータの値を見つける必要があります。
![]()
そして
![]()
式の。この場合、
![]()
変数に対応する
![]()
そして
![]()
は2番です。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-909b3b4a2f976c165f160a6765b3ed9d_l3.png)
の値を置き換えることによって注目すべき製品を計算します。
![]()
そしての
![]()
式の中で:

違いの立方体
差の 3 乗、または減算の 3 乗は、負の符号が付いた項を持つ 3 のべき乗の二項です。したがって、この注目すべき製品タイプの数式は(ab) 3です。
差の 3 乗 (または減算) の公式は次のとおりです。

明らかに、この公式の証明は、和の 3 乗の注目すべき積の証明と非常に似ています。ただし、この場合は、負の 3 乗二項式から開始します。
![]()
明らかに、前の増強は係数の積に分解できます。
![]()
その二乗を掛けると:
![]()
したがって、注目すべき二乗恒等式で研究したように、二項
![]()
これは、差の二乗の公式を使用して計算できます。
![]()
ここで、2 つの多項式の積を生成します。
![Rendered by QuickLaTeX.com \begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-627a273de8fff974f4a14a32fcee90b8_l3.png)
最後のステップは、類似した用語をグループ化することです。
![]()
したがって、減算二項式を立方体に乗じた注目すべき恒等式の公式が検証されます。
![]()
したがって、3 まで上げられた差 (または減算) は、最初の値の 3 倍から 2 番目の値の 2 乗の 3 倍を引いたもの、さらに 1 番目の値の 3 倍と 2 番目の平方根の 3 倍から 2 番目の 3 乗を引いたものに等しくなります。
例:
- 対応する式を使用して、次の 3 乗二項 (差) を計算します。
![]()
この演習では、正の要素と負の要素を持つペアがあります。したがって、差の 3 乗を求める公式を使用する必要があります。
![]()
まず、いつものように、未知数の値を特定します
![]()
そして
![]()
式の。この場合
![]()
単項式を表します
![]()
そして
![]()
は二項式の独立項、つまり 2 です。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a792ec6dead8466ec6a2cb2a43d9fab4_l3.png)
パラメータに注意してください
![]()
数値の負符号なしで、単純に 2 に等しくなります。公式を適切に適用するには、この点に留意することが重要です。
最後に、次の値を置くことで注目すべきアイデンティティを見つけます。
![]()
そしての
![]()
式の中で:

注目すべきアイデンティティの概要表
要約すると、これまでに見たすべての注目すべきアイデンティティ (または製品) をまとめた表を作成したので、それらを研究しやすくなります。 😉

注目すべきアイデンティティ (または製品) の解決された演習
注目に値する製品または注目に値する等価性とも呼ばれる注目に値するアイデンティティの概念を完全に理解できるように、段階的に解決するいくつかの演習を用意しました。それらを実行してみて、演習の解決策がうまくできたかどうかを確認できます。
⬇⬇ ご質問はすべて、以下のコメント欄で質問できることを忘れないでください。 ⬇⬇
演習 1
次の注目すべき恒等式 (平方和) を展開します。
![]()
![]()
![]()
![]()
問題内の注目すべき恒等式はすべて二乗和であるため、この場合は常に同じ公式を適用する必要があります。
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-067fdf38612ca481db587bda479cab24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
演習 2
次の注目すべき製品を開発します (差の二乗)。
![]()
![]()
![]()
![]()
この演習で注目すべき積はすべて二乗減算であるため、適用する必要がある公式は 1 つだけです。
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14d502eda968fe82617b4403cd9c4722_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c22d520301280872e645f5683a2fba8e_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95c7c481a96b20b700bd2253c90f0c0d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cea9fa89580d3d9d9df7fd93cca2b89_l3.png)
演習 3
次の注目すべき等式 (和と差の積) を展開します。
![]()
![]()
![]()
![]()
この演習で注目すべきすべての等式は和と差の乗算であるため、これらはすべて同じ公式で解けます。
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-826c4aec8f005514a14cdc8555c084c4_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6793239af84413fb9408c2cb6033e5ce_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-630b94cf4be27c5f7b9c87651368634d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-80c5451e407a2c0e670c6cb22a74043c_l3.png)
演習 4
次の注目すべきアイデンティティをすべて解決します。
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c65875e01d82840e30ae85d803d45e90_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04e0bcf5df362d320cfdb2f87cdc6ddc_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc3f7dc61f7c44a60c01e0a95de278fa_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4d4a0c86d26820881eb65cb92c3679a_l3.png)
![Rendered by QuickLaTeX.com \text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-432c4ae0f050bec15e3fa52f426698ec_l3.png)
演習 5
次の注目すべき製品を計算します。
![]()
![]()
![]()
![]()
問題の注目すべき積をすべて見つけるには、場合に応じて和と差の 3 乗の公式を適用する必要があります。
![]()
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14695fb807e2df89352fdd1c1dced2ee_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5be0d584351feb0bef5572ca5c9e159a_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44f9c3283dad97321644c6e559f64ff_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-156e7619e4d6ef129f04250af8197d2e_l3.png)
演習 6
次の注目すべき等式を解きます。
![]()
![]()
![]()
![]()
これらの重要な恒等式をすべて解決するには、次のような三項式の 2 乗の公式を使用する必要があります。
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-749dc45e7a00d7122d62b774706bdcc0_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1f51f18b3c1118b6e8e3acc3441b0ec_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-49c6496bf684296d315fc96d9cb5857e_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7cd08035d8402c27c411bcf5b30216cb_l3.png)
演習 7
根と分数を使用して次の注目すべき恒等式を計算します (高難易度)。
![]()
![]()
![]()
![]()
セクション A) は二乗減算で構成されているため、これを解くには対応する式を適用する必要があり、さらに、根が二乗されると単純化されることを覚えておく必要があります。
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-999e71bf062ea313780439abaf2b4295_l3.png)
セクション B) は減算による加算を扱い、単項式には分数係数があり、この注目すべき積は減算による加算の式と分数の性質を使用して決定する必要があります。
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-24593bac7bd4a9837e1f18fef4f9c38e_l3.png)
セクション C) の注目すべき等式は、和を 2 まで上げたものであり、同様に分数で構成されています。したがって、これを計算するには、平方和の公式と分数の性質を使用する必要があります。
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
最後の注目すべき恒等式は、無理係数を使用した和と差を扱うため、和と差の公式を適用して平方根を単純化します。
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c540e4315e9e84faaa2ff656c4eec21_l3.png)
その他の注目すべき ID タイプ
上で説明した注目すべきアイデンティティはすべて、最も一般的に使用されているものです。ただし、数学では、さまざまな目的に使用されるため、知っておくと興味深い他の注目すべき製品タイプがあります。
立方体の和
立方体の和は、2 つの項が正であり、さらにその立方根が正確である二項式に対応します。したがって、立方体の和の代数式はa 3 +b 3となります。

この注目すべき積の公式は、多項式を因数分解するために使用されます。つまり、この公式を通じて、多項式を二項と三項の積に変換します。
これがどのように行われるかがわかります。この注目すべきアイデンティティの適用例を次に示します。
![]()
確かに、前の式は立方体の加算で構成されています。なぜなら、単項式の立方根は
![]()
は正確です (10 進数は表示されません)。数字の 8 も同様です。
![]()
![]()
![]()
したがって、完全立方体の和の公式を使用して、三次式を二項式と三項式の積に変換できます。
![]()
![Rendered by QuickLaTeX.com \begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f30ea5f0f7ef1b89a16f1d00e54d063c_l3.png)
立方体の違い
立方体の差 (または減算) は、立方根が正確な正の項と負の項で構成される二項式です。つまり、立方体の差分は、 a 3 -b 3の形で表される。

この注目すべき ID タイプがどのように解決されるかを確認できるように例を作成してみましょう。
![]()
両方の単項式の立方根なので、立方体の違いです。
![]()
27 が正しいので、
![]()
![]()
![]()
したがって、完全立方体の差の公式を使用して、二項を因数分解することができます。
![]()
![Rendered by QuickLaTeX.com \begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-342a448f849bf2856ad9a5394733faeb_l3.png)
共通項を持つ二項積
この注目すべき積は、共通項を持つ 2 つの二項式の積を 2 次多項式に変換するために使用されます。

このタイプの注目すべき製品の精巧な例を次に示します。
![Rendered by QuickLaTeX.com \begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8447db6a2246c09b2e7be29f8050a3d6_l3.png)
さらなるアイデンティティ
注目に値するアイデンティティは、最も一般的であるため最も有名ですが、他の名前を持つアイデンティティも同様に存在することに注意してください。興味がある場合に備えて、他のあまり知られていないアイデンティティのリストを以下に示します。
- ラグランジュ恒等式:
-
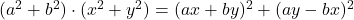
-
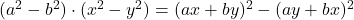
- ルジャンドルのアイデンティティ:
-
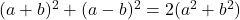
-
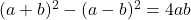
-
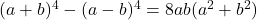
- アルガンドの正体:
-
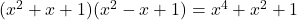
- ガウス恒等式:
-
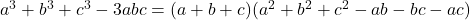
-
![Rendered by QuickLaTeX.com a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6b2da7d99ade85355a54bee45b79a9f_l3.png)
注目の ID アプリ
ここまで理解できたということは、注目すべき恒等式を使用して計算を行う方法をすでに知っていることを意味します。明るい!しかし実際には…注目すべきアイデンティティとは何でしょうか?そして、注目すべきアイデンティティはいつ使用されるのでしょうか?
この記事全体で見てきたように、注目すべきアイデンティティの主な目的は計算を簡素化することです。つまり、優れた製品のおかげで、難しい演算を実行することなく、複雑な多項式の特定の累乗を直接解くことができます。
ただし、注目すべき等式には、多項式の因数分解や平方の完成など、他の機能もあります。次に、これらの各アプリケーションが何で構成されているかを見ていきます。
多項式の因数分解
いくつかの非常に特殊なタイプの多項式は、注目すべき恒等式で因数分解できます。たとえば、完全二乗である (平方根が正確である) 2 つの項で構成される多項式を見つけた場合、和と差の積という注目すべき等式を使用してそれを因数分解できます。
![]()
![]()
同様に、加算または減算の 2 乗の注目すべき恒等式を尊重する三項式は因数分解できます。
![]()
![]()
![]()
![]()
同様に、多項式が因数分解されると、その多項式の根 (またはゼロ) を見つけることができます。それでも、この概念は理解するのが少し複雑なので、より興味がある場合は、全文を説明した記事があるため、Web サイト (右上) の検索エンジンで説明を検索することをお勧めします。
正方形の完成
平方完成は、二次三項式を平方和プラス (またはマイナス) 数値に変換するために使用される数学的手順です。
任意の三項式が与えられた場合:
![]()
次に、三項式は次の式に変換できます。
![]()
ここでパラメータは
![]()
そして
![]()
は次の式で計算されます。
![]()
あなたにはそうは思えないとしても、これら 2 つの公式は注目すべきアイデンティティから導き出されます。素晴らしい製品のおかげで、正方形が完成することができます。
例として、この手順を次の三項式に適用します。
![]()
パラメータを計算します
![]()
そして
![]()
![]()
![]()
したがって、多項式は次のようになります。
![]()