このページでは、対角化可能な行列とは何か、対角化できる場合とできない場合、行列を対角化する方法、これらの特定の行列のアプリケーションとプロパティなど、対角化可能な行列に関するすべてを説明します。さらに、段階的に解決するいくつかの演習も用意されているため、対角化がどのように行われるかを練習して完全に理解することができます。最後に、コンピューター プログラム MATLAB は非常に頻繁に使用されるため、行列の対角化を実行する方法も学びます。
対角化可能な行列とは何ですか?
以下で説明するように、行列の対角化は線形代数の分野で非常に役立ちます。これが、多くの人が疑問に思う理由です…行列の対角化とは何ですか?さて、対角化可能な行列の定義は次のとおりです。
対角化可能行列は、対角行列、つまり主対角を除いてゼロで満たされた行列に変換できる正方行列です。行列の対角化は次のように分類されます。
![]()
または同等の、
![]()
金
![]()
は対角化する行列です。
![]()
列が次の固有ベクトル (または固有ベクトル) である行列です。
![]()
、
![]()
その逆行列と
![]()
の固有値 (または固有値) によって形成される対角行列です。
![]()
。
マトリックス
![]()
は基数変更行列として機能するため、実際にはこの式を使用して基数を行列に変更します
![]()
, そのため、行列は対角行列になります (
![]()
) 新しい拠点に。
したがって、行列は
![]()
そしてマトリックス
![]()
これらは類似した行列です。そして明らかに、
![]()
これは、正規行列または非縮退行列です。
行列を対角化できるのはいつですか?
すべての行列を対角化できるわけではありません。特定の特性を満たす行列のみを対角化できます。行列が対角化可能かどうかは、さまざまな方法で確認できます。
- 次数nの正方行列は、 n 個の線形に独立した固有ベクトル (または固有ベクトル)を持つ場合、つまりこれらのベクトルが基底を形成する場合、対角化可能です。これは、マトリックスがあるためです。

行列を対角化するために使用される、行列の固有ベクトルによって形成されます。固有ベクトルが LI であるかどうかを知るには、行列の行列式が次であれば十分です。

は 0 とは異なります。これは、行列のランクが最大であることを意味します。
![]()
- 固有値と固有ベクトルの特性は、異なる固有値の固有ベクトルが線形独立であることです。したがって、行列のすべての固有値が一意であれば、行列は対角化可能です。
- 行列が対角行列に収まるかどうかを判断する別の方法は、代数的および幾何学的多重度を使用することです。代数的多重度は、固有値 (または固有値) が繰り返される回数であり、幾何学的多重度は、主対角上の固有値を減算した行列のカーネル (または カーネル) の次元です。したがって、各固有値の代数多重度が幾何多重度に等しい場合、行列は対角化可能です。
![]()
![]()
![]()
![]()
- 最後に、実数による対称行列の対角化を保証するスペクトル定理という定理があります。言い換えれば、実数の対称行列はすべて対角化可能です。
行列を対角化する方法
行列を対角化する手順は、行列の固有値 (または固有値) と固有ベクトル (または固有ベクトル) を見つけることに基づいています。このため、行列の固有値 (または固有値) と固有ベクトル (または固有ベクトル) の計算方法を習得することが重要です。リンクをクリックすると、その計算方法を思い出すことができます。ここでは、それらを見つける方法と、計算をはるかに簡単にするいくつかのトリックをステップバイステップで説明します。さらに、練習できる解決済みの演習も見つかります。
次の方法を使用すると、2×2、3×3、4×4 などの任意の次元の行列を対角化できます。行列を対角化するには次の手順に従います。
- 行列の固有値(または固有値)を取得します。
- 各固有値に関連付けられた固有ベクトルを計算します。
- マトリックスの構築

、その列は対角化される行列の固有ベクトルです。
- 行列が対角化できることを確認します (前のセクションで説明した条件のいずれかを満たしている必要があります)。
- 対角行列を構築する
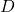
、その要素は、ステップ 1 で見つかった固有値である主対角上の要素を除いてすべて 0 です。
警告:行列の固有ベクトル
![]()
任意の順序で配置できますが、対角行列の固有値は
![]()
これらは同じ順序で配置する必要があります。たとえば、対角行列の最初の固有値
![]()
行列の最初の列の固有ベクトルに対応するものでなければなりません
![]()
。
以下に、練習できる段階的な行列の対角化演習をいくつか示します。
行列の対角化演習を解決しました
演習 1
次の次元 2×2 の正方行列を対角化します。
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix}2&2\\[1.1ex] 1&3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13b9f5c8b5a381c9661aa4ee2e0b7b63_l3.png)
まず行列 A の固有値を決定する必要があります。したがって、次の行列式を解くことによって特性方程式を計算します。
![Rendered by QuickLaTeX.com \displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2- \lambda &2\\[1.1ex] 1&3-\lambda \end{vmatrix} = \lambda^2-5\lambda +4](https://mathority.org/wp-content/ql-cache/quicklatex.com-f652aa2ef8cd55100970fef7fbf30e60_l3.png)
次に、特性多項式の根を計算しましょう。
![Rendered by QuickLaTeX.com \displaystyle \lambda^2-5\lambda +4=0 \ \longrightarrow \ \begin{cases} \lambda = 4 \\[2ex] \lambda = 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c53bbe295e0f77d1cdaa183e9341567d_l3.png)
固有値が取得されたら、それぞれに関連付けられた固有ベクトルを計算します。まず、固有値 1 に対応する固有ベクトル:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}1&2\\[1.1ex] 1&2\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83d7b7d31a262f6e0844a0a9f5098e11_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] x+2y = 0\end{array}\right\} \longrightarrow \ x=-2y](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ea3248973afa32a42f87b20e0c5ddc9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}-2 \\[1.1ex] 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73435e1b8c9d689ec17255f087e978f0_l3.png)
次に、固有値 4 に関連付けられた固有ベクトルを計算します。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}-2&2\\[1.1ex] 1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d9c6b33d8fad6974d366ce088800b92a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} -2x+2y = 0 \\[2ex] x-y = 0\end{array}\right\} \longrightarrow \ y=x](https://mathority.org/wp-content/ql-cache/quicklatex.com-d68533e14c844cf5bd4ee1965533ee6f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}1 \\[1.1ex] 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f3cac5769795f1730fcbf118fdfbbc3_l3.png)
マトリックスを構築します
![]()
、行列の固有ベクトルによって形成されます。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-46dde85eb30324e4dfec09cbb802853e_l3.png)
すべての固有値が異なるため、行列 A は対角化可能です。したがって、対応する対角行列は、主対角線上に固有値を持つものになります。
![Rendered by QuickLaTeX.com \displaystyle D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1e0329677969153d43ce741754dc6924_l3.png)
固有値は、固有ベクトルが行列に配置されるのと同じ順序で配置する必要があることに注意してください。
![]()
。
結論として、基底変化行列と対角化行列は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ea54fe9e11d849c2896cc312df404ba_l3.png)
演習 2
次の次数 2 の正方行列を対角化します。
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix}3&4\\[1.1ex] -1&-2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f61af0f4b152be75cc74b7733b2de076_l3.png)
まず行列 A の固有値を決定する必要があります。したがって、次の行列式を解くことによって特性方程式を計算します。
![Rendered by QuickLaTeX.com \displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3- \lambda &4\\[1.1ex] -1&-2-\lambda \end{vmatrix} = \lambda^2-\lambda -2](https://mathority.org/wp-content/ql-cache/quicklatex.com-31024cc955652299f8933e082f934f15_l3.png)
次に、特性多項式の根を計算しましょう。
![Rendered by QuickLaTeX.com \displaystyle \lambda^2-\lambda -2=0 \ \longrightarrow \ \begin{cases} \lambda = -1 \\[2ex] \lambda = 2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-341b01a85529d26a506ebc9336221dca_l3.png)
固有値が取得されたら、それぞれに関連付けられた固有ベクトルを計算します。まず、固有値 -1 に対応する固有ベクトル:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}4&4\\[1.1ex] -1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2728e62bfb96bb9106b0f7791ba9c5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} 4x+4y = 0 \\[2ex] -x-y = 0\end{array}\right\} \longrightarrow \ x=-y](https://mathority.org/wp-content/ql-cache/quicklatex.com-0515ba12f6ad51cc35cc785697498b78_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0059538893e6c8439792228733f803de_l3.png)
次に、固有値 2 に関連付けられた固有ベクトルを計算します。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}1&4\\[1.1ex] -1&-4\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-aff94f6ac5c08a408abcb42f4262ac0a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} x+4y = 0 \\[2ex] -x-4y = 0\end{array}\right\} \longrightarrow \ x=-4y](https://mathority.org/wp-content/ql-cache/quicklatex.com-2930b2bf0ef86ea8be216bafe5c3aa32_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}-4 \\[1.1ex] 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ede8a2a2803fc807b34db04326f5e1cf_l3.png)
マトリックスを構築します
![]()
、行列の固有ベクトルによって形成されます。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-990ff35382717a4644e33e8630777237_l3.png)
すべての固有値は互いに異なるため、行列 A は対角化可能です。したがって、対応する対角行列は、主対角上の固有値を含む行列になります。
![Rendered by QuickLaTeX.com \displaystyle D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cb2a5e7884d62f8ed609465e289fa70e_l3.png)
固有値は、固有ベクトルが行列に配置されるのと同じ順序で配置する必要があることに注意してください。
![]()
。
結論として、基底変化行列と対角化行列は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1\end{pmatrix} \qquad D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-60358333f16516ac0d64d12891ef6ea5_l3.png)
演習 3
次の次元 3×3 の正方行列を対角化します。
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix}2&0&2\\[1.1ex] -1&2&1\\[1.1ex] 0&1&4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8fc8797c8c0354ff540e340b82cb9258_l3.png)
最初のステップは、行列 A の固有値を見つけることで構成されます。したがって、次の行列の行列式を解くことで特性方程式を計算します。
![Rendered by QuickLaTeX.com \displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&0&2\\[1.1ex] -1&2-\lambda&1\\[1.1ex] 0&1&4-\lambda \end{vmatrix} = -\lambda^3+8\lambda^2-19\lambda+12](https://mathority.org/wp-content/ql-cache/quicklatex.com-280aeb93bd229f34fe255f368390ae6a_l3.png)
次に、特性多項式の根を計算する必要があります。これは 3 次多項式であるため、ルフィニの法則を適用します。
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{r|rrrr} & -1&8&-19& 12 \\[2ex] 1 & & -1&7&-12 \\ \hline &-1\vphantom{\Bigl)}&7&-12&0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9fc16d8c9420ece9152119b48f249df9_l3.png)
そして、得られた多項式の根を求めます。
![Rendered by QuickLaTeX.com \displaystyle -\lambda^2+7\lambda -12=0 \ \longrightarrow \ \begin{cases} \lambda = 3 \\[2ex] \lambda = 4 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e07297a9da80525b94e7af1914f403be_l3.png)
したがって、行列の固有値は次のようになります。
![]()
固有値が見つかったら、それぞれに関連付けられた固有ベクトルを計算します。まず、固有値 1 に対応する固有ベクトル:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}1&0&2\\[1.1ex] -1&1&1\\[1.1ex] 0&1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50b6b424d6465f208981f3f89213bb2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} x+2z = 0 \\[2ex] -x+y+z = 0\\[2ex] y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=-2z \\[2ex] y = -3z \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8c810793db36ac827b71d01324760cee_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}-2 \\[1.1ex] -3 \\[1.1ex] 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-88fc97c4f3a0e5a6d79978e154230e22_l3.png)
次に、固有値 3 に関連付けられた固有ベクトルを計算します。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}-1&0&2\\[1.1ex] -1&-1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-05bcbb328be85066bb142c990bbfad99_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} -x+2z = 0 \\[2ex] -x-y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=2z \\[2ex] y = -z \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-656b90b758fe5ab6178efdfcbef399ef_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}2 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-33033f69510447ef3684a67e835bd578_l3.png)
最後に、固有値 4 に関連付けられた固有ベクトルを計算します。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}-2&0&2\\[1.1ex] -1&-2&1\\[1.1ex] 0&1&0\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f455bc39f72a9b8141ba714bd72a0e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} -2x+2z = 0 \\[2ex] -x-2y+z = 0\\[2ex] y = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=z \\[2ex] y = 0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dd0ebc259ff2665ef3c4c3a3b1692e2e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-308b2f0f597fcc084d8d06d6c45fd3e5_l3.png)
マトリックスを構築します
![]()
、行列の固有ベクトルによって形成されます。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f1f57ccbb391403b5e4af625900516cc_l3.png)
すべての固有値は互いに異なるため、行列 A は対角化可能です。したがって、対応する対角行列は、主対角線上に固有値を持つものになります。
![Rendered by QuickLaTeX.com \displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e88d2a690d31a9ca772d185078f69d3f_l3.png)
固有値は、固有ベクトルが行列に配置されるのと同じ順序で配置する必要があることに注意してください。
![]()
。
つまり、基底変化行列と対角化行列は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1\end{pmatrix} \qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6fdff19d2d1e3f58ba1898dc456711d_l3.png)
演習 4
可能であれば、次の 3 次の正方行列を対角化します。
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix}-1&3&1\\[1.1ex] 0&2&0\\[1.1ex] 3&-1&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-628e7e12a0d8ccde5bb1fb2626663910_l3.png)
最初のステップは、行列 A の固有値を見つけることで構成されます。したがって、次の行列の行列式を解くことで特性方程式を計算します。
![Rendered by QuickLaTeX.com \displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}-1-\lambda&3&1\\[1.1ex] 0&2-\lambda&0\\[1.1ex] 3&-1&1-\lambda \end{vmatrix} = -\lambda^3+2\lambda^2+4\lambda-8](https://mathority.org/wp-content/ql-cache/quicklatex.com-30678afffed54546baac35a9eeda7e74_l3.png)
次に、最小多項式の根を計算する必要があります。これは 3 次多項式であるため、ルフィニの規則を適用して因数分解します。
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{r|rrrr} & -1&2&\phantom{-}4& -8 \\[2ex] 2 & & -2&0&8 \\ \hline &-1\vphantom{\Bigl)}&0&4&0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1022b20e607032ce89202906035a1315_l3.png)
そして、得られた多項式の根を求めます。
![Rendered by QuickLaTeX.com \displaystyle -\lambda^2+4=0 \ \longrightarrow \ \begin{cases} \lambda = +2 \\[2ex] \lambda = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef5a87ff07eca3feb9798f85cd0b21c7_l3.png)
したがって、行列の固有値は次のようになります。
![]()
-2 の固有値は単純な代数多重度ですが、2 の固有値は 2 倍の多重度です。
固有値が見つかったら、それぞれに関連付けられた固有ベクトルを計算します。まず、固有値 -2 に対応する固有ベクトル:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}1&3&1\\[1.1ex] 0&4&0\\[1.1ex] 3&-1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f548e75ebc3648368d043737d26c3141_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} x+3y+z = 0 \\[2ex] 4y = 0\\[2ex] 3x-y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] x = -z \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eda9945255b333b217a9c40fc90fb632_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] -1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e79ea01eaeac74b4cf803f470fbb329b_l3.png)
次に、固有値 2 に関連付けられた固有ベクトルを計算してみましょう。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}-3&3&1\\[1.1ex] 0&0&0\\[1.1ex] 3&-1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-53c61e86f8559cae71cca6a111379645_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} -3x+3y+z = 0 \\[2ex] 0= 0\\[2ex] 3x-y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] z=3x \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9de45793fef0fd80dff4c8013e9d444d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e90d075bde6188e524147bdd92aa203d_l3.png)
固有値 2 は 2 回繰り返されるため、部分空間 (または固有空間) 方程式を満たす別の固有ベクトルを計算する必要があります。
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] -3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-517e77ee4e68f74541ce05ff82fe8188_l3.png)
マトリックスを構築します
![]()
、行列の 3 つの固有ベクトルによって形成されます。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a457d6a8a6af3a42596803162118e90_l3.png)
ただし、固有値 2 を持つ 2 つの固有ベクトルは明らかに相互の線形結合であるため、3 つのベクトルは線形独立ではありません。これは、行列の行列式によっても証明できます。
![]()
は 0 に等しい (行がゼロでいっぱい):
![Rendered by QuickLaTeX.com \displaystyle \text{det}(P) = \begin{vmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-eef0b8cbbbfc27e1f11bee978f009064_l3.png)
したがって、固有ベクトルは線形従属であるため、行列 A は対角化できません。
演習 5
可能であれば、次のサイズ 3×3 の正方行列を対角化します。
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix}3&0&0\\[1.1ex] 0&2&1\\[1.1ex] 0&1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c00122db1c4520c4ff5907ba29c05647_l3.png)
最初のステップは、行列 A の固有値を見つけることで構成されます。したがって、次の行列の行列式を解くことで特性方程式を計算します。
![Rendered by QuickLaTeX.com \displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0bc2d83752a7ea5c3532047677b123b4_l3.png)
最初の行は 3 を除いて完全にゼロで構成されているため、これを利用して余因子 (または随伴関数) によって行列の行列式を解きます。
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}& = (3-\lambda)\cdot \begin{vmatrix} 2-\lambda&1\\[1.1ex]1&2-\lambda \end{vmatrix} \\[3ex] & = (3-\lambda)[\lambda^2 -4\lambda +3] \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f27c9abc6047b2289c6dca75524c36b1_l3.png)
次に、特性多項式の根を計算する必要があります。括弧を乗算すると 3 次多項式が得られるため、乗算しない方がよいでしょう。一方、2 つの因子を別々に解決すると、固有値を取得するのが簡単になります。
![Rendered by QuickLaTeX.com \displaystyle (3-\lambda)[\lambda^2 -4\lambda +3]=0 \ \longrightarrow \ \begin{cases} 3-\lambda=0 \ \longrightarrow \ \lambda = 3 \\[2ex] \lambda^2 -4\lambda +3=0 \ \longrightarrow \begin{cases}\lambda = 1 \\[2ex] \lambda = 3 \end{cases} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-51bd286d6b714a75da7b952b21b01000_l3.png)
したがって、行列の固有値は次のようになります。
![]()
固有値が見つかったら、それぞれに関連付けられた固有ベクトルを計算します。まず、固有値 1 に対応する固有ベクトル:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}2&0&0\\[1.1ex] 0&1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e830c9d5e670fac1f34cbd469a11255_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} 2x = 0 \\[2ex] y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=0 \\[2ex] y = -z \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a2afb8e9c13b45197cd1b96c25dd7f9c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}0 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e82a93f938d6438a3f8caf32715cc3d8_l3.png)
次に、固有値 3 に関連付けられた固有ベクトルを計算します。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}0&0&0\\[1.1ex] 0&-1&1\\[1.1ex] 0&1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e32cf06d1621a90bae143448d4fa348_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} 0 = 0 \\[2ex] -y+z = 0\\[2ex] y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=z \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d52817f384fe99c1ecc4dce8034d138f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}0 \\[1.1ex] 1 \\[1.1ex] 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4f56725fbe621b829ccd3de6e289af91_l3.png)
固有値 3 が 2 回繰り返されるため、固有空間方程式を満たす別の固有ベクトルを計算する必要があります。
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d53a91ff3ef0a02d62956e7517bff871_l3.png)
マトリックスを構築します
![]()
、行列の固有ベクトルによって形成されます。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-01c9824b06a22d012e8d7f7d10b3d411_l3.png)
演習 4 とは異なり、この場合、固有値 3 の代数多重度は 2 倍ですが、3 つの線形独立ベクトルを形成することができました。これは、行列の行列式を見ることで検証できます。
![]()
0 とは異なる結果が得られます。
![Rendered by QuickLaTeX.com \displaystyle \text{det}(P) = \begin{vmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{vmatrix} =-2 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-5b64f45987701e73cd19b7ca0183e20f_l3.png)
したがって、行列 A の対角分解を実行できます。そして、対応する対角行列は、主対角に固有値を持つものです。
![Rendered by QuickLaTeX.com \displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-428f628ac9ba4c7ae6eb615b0e726735_l3.png)
固有値は、固有ベクトルが行列に配置されるのと同じ順序で配置する必要があることに注意してください。
![]()
。
つまり、行列を対角化するために必要な基底変化行列とその対角化形式は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}\qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6fc326a197ddeb33da66d0ecbb5f3b1_l3.png)
演習 6
可能であれば、次の 4×4 次元の行列の対角化を実行します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b25cef0f514564a0206c2f8a588bd346_l3.png)
最初のステップは、行列 A の固有値を見つけることで構成されます。したがって、次の行列の行列式を解くことで特性方程式を計算します。
![Rendered by QuickLaTeX.com \displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7cacf7f3b5f63ab816368aaa866e5762_l3.png)
この場合、行列式の最後の列は 1 つの要素を除いてゼロのみで構成されているため、これを利用して、この列を介して余因子によって行列式を計算します。
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}& = (5-\lambda)\cdot \begin{vmatrix}2-\lambda&1&2\\[1.1ex] 1&-3-\lambda&1\\[1.1ex] 0&-1&-\lambda\end{vmatrix}\\[3ex] & = (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda] \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4211dd57b179125aa12310419b051ccb_l3.png)
次に、特性多項式の根を計算する必要があります。括弧の積を計算すると 4 次の多項式が得られるため、計算しない方がよいでしょう。ただし、2 つの要素を別々に解決すると、固有値を計算する方が簡単になります。
![Rendered by QuickLaTeX.com \displaystyle (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda]=0 \ \longrightarrow \ \begin{cases} 5-\lambda=0 \ \longrightarrow \ \lambda = 5 \\[2ex] -\lambda^3 -\lambda^2 +6\lambda =0 \ \longrightarrow \ \lambda(-\lambda^2 -\lambda +6) =0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c85f64406d449b4f23e6bbc31ee093b7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \lambda(-\lambda^2 -\lambda +6)=0 \ \longrightarrow \ \begin{cases} \lambda=0 \\[2ex] -\lambda^2 -\lambda +6=0 \ \longrightarrow \ \begin{cases} \lambda=2 \\[2ex] \lambda = -3 \end{cases}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96a7a939f5e7d075a94581b2354f7c79_l3.png)
したがって、行列の固有値は次のようになります。
![]()
すべての固有値が見つかったら、固有ベクトルに進みます。固有値 0 に関連付けられた固有ベクトルを計算します。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-48e7a88c722f93154455a7d3a139e9e0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} 2w+x+2y = 0 \\[2ex] w-3x+y = 0\\[2ex] -x=0 \\[2ex] 5z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=0 \\[2ex] z=0 \\[2ex]w=-y \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bd06b2978a9da318f23d71c96d5d028e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e6cb2192b1819fcd5216e1ad0b37346_l3.png)
固有値 -3 に関連付けられた固有ベクトルを計算します。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5&1&2&0\\[1.1ex] 1&0&1&0\\[1.1ex] 0&-1&3&0\\[1.1ex] 0&0&0&8\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bb4e1e57896d33ad465b139fee1f0069_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} 5w+x+2y = 0 \\[2ex] w+y = 0\\[2ex] -x+3y=0 \\[2ex] 8z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=-y \\[2ex]x=3y \\[2ex] z=0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0190aad5028c9efdaebb2226b863104d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 3 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d4c0c3b06a7cdb14076a2d1dc0eb395_l3.png)
固有値 2 に関連付けられた固有ベクトルを計算します。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 0&1&2&0\\[1.1ex] 1&-5&1&0\\[1.1ex] 0&-1&-2&0\\[1.1ex] 0&0&0&3\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7263a76e7855eedadeecb32ac4e3a097_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] w-5x+y = 0\\[2ex] -x-2y=0 \\[2ex] 3z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=-2y \\[2ex] w=-11y \\[2ex] z=0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1655d285c99ec5c316ac5b56f7a2bfb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}-11 \\[1.1ex] -2 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b72552cd6d30c1f940b2c8ebefa911f_l3.png)
固有値 5 に関連付けられた固有ベクトルを計算します。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} -3&1&2&0\\[1.1ex] 1&-8&1&0\\[1.1ex] 0&-1&-5&0\\[1.1ex] 0&0&0&0\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cad6a424d357b8ab8ad0dbf5b6a9a1fe_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l} -3w+x+2y = 0 \\[2ex] w-8x+y = 0\\[2ex] -x-5y=0 \\[2ex] 0=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=x=y=0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3531f26937c3668fb457e0af0cf8761d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle v = \begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0 \\[1.1ex]1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-633b2852390bdc22c60e2aaf38b6ab2c_l3.png)
マトリックスを作ります
![]()
、行列の固有ベクトルで構成されます。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d01ab11cb87f40e42c259bf37e95130f_l3.png)
すべての固有値は互いに異なるため、行列 A は対角化可能です。したがって、対応する対角行列は、主対角線上に固有値を持つものになります。
![Rendered by QuickLaTeX.com \displaystyle D= \begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8174826f72dc49491c2884f32f54febf_l3.png)
固有値は、行列内での固有ベクトルの配置と同じ順序で配置する必要があることに注意してください。
![]()
。
要約すると、行列 A と対角形式の行列を対角化するために必要な基本的な行列の変更は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix} \qquad D=\begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-029be0f37d9f5846758b7dbb1e25c8fc_l3.png)
対角化可能な行列の応用
ここまで読んだ方は、おそらく「対角化可能な行列とは何ですか?」と疑問に思っているでしょう。
そうですね、対角化可能な行列は非常に便利で、数学で広く使用されています。その理由は、対角行列は実質的にゼロでいっぱいであるため、計算がはるかに簡単になるためです。
この明確な例は、対角化可能な行列の累乗です。その結果は次の式で簡略化されます。
![]()
この等価性は帰納法によって簡単に証明できます。したがって、マトリックスを上げるだけで十分です
![]()
出展者へ。これは対角行列であるため、演算は主対角の各項を指数化することになります。
![]()
対角化可能な行列の累乗の例
よりよく理解するために、例として対角化可能な行列の累乗を計算します。
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix}2&0\\[1.1ex] 3&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3544a0199a7c277c7497a042deee07ce_l3.png)
基本的な変更マトリックス
![]()
、その固有ベクトルと対角化された行列によって形成されます。
![]()
は、独自の値で構成され、次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle P = \begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3d5f3ac30ba6b6ac40e819e86daad73e_l3.png)
したがって、例を挙げると、行列 A を 7 に累乗すると、次と等価になります。
![]()
![Rendered by QuickLaTeX.com \displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\left.\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\right.^{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c0cbd00c0e1c04f294d8ff5413894e5_l3.png)
ここで行列を逆にしてみましょう
![]()
![Rendered by QuickLaTeX.com \displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9747b331e1548549fa7a171695729eec_l3.png)
マトリックスのパワーを解きます
![]()
![Rendered by QuickLaTeX.com \displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1^7&0\\[1.1ex] 0&2^7\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-147918af8d66f941dcd70444b7e0d5a2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&128\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-27c7f9dee1b20761a9845457099573cf_l3.png)
そして最後に、行列の乗算を実行します。
![Rendered by QuickLaTeX.com \displaystyle \bm{A^7=}\begin{pmatrix}\bm{128}&\bm{0}\\[1.1ex] \bm{381}&\bm{1}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f77fa7a83f343c5723afa0a3fde981cc_l3.png)
これまで見てきたように、同じ行列を連続して 7 回乗算するよりも、対角行列を使用してべき乗を計算する方が便利です。次に、さらに大きな指数値を想像してください。
対角化可能な行列のプロパティ
このタイプのマトリックスの特徴は次のとおりです。
- マトリックスの場合

は対角化可能です。

。
- ほとんどすべての行列は複雑な環境で対角化できます
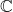
。ただし、以下では決して対角化できない例外があります。
- マトリックスの場合

が直交行列である場合、行列と言います。

は直交対角化可能であるため、方程式は次のように書き換えることができます。
![]()
- 行列は、正規行列である場合に限り、ユニタリ行列によって対角化できます。
- 2 つの対角化可能な行列が与えられた場合、同時に対角化できる場合、つまり、固有ベクトル (または固有ベクトル) の同じ正規直交基底を共有する場合に限り、それらは可換です。
- 準同型性が対角化可能である場合、それは類似性 によって対角化可能であると言います。ただし、すべての準同型性が対角化可能であるわけではありません。つまり、準同型性の対角化が保証されているわけではありません。
同時対角化
行列のセットは、このセット内の任意の行列を対角化するための基礎として機能する可逆行列が存在する場合、同時に対角化可能であると言われます。言い換えれば、2 つの行列が同じ固有ベクトルに基づいて対角化される場合、これはそれらが同時に対角化可能であることを意味します。
さらに、行列の対角化のプロパティでコメントしたように、2 つの行列が同時に対角化できる場合、それらは互いに可換でなければなりません。
たとえば、次の 2 つの行列は可換であるため、同じ固有ベクトルに基づいて対角化されます。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2&0 \\[1.1ex] 1&-1 \end{pmatrix} \qquad B=\begin{pmatrix}3&0\\[1.1ex] 1&0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c215d8b5d9ae75dbd069c6b6d39886dd_l3.png)
たとえ同じ固有ベクトルを持っていたとしても、それは同じ固有値を持つことを意味するわけではありません。実際、上記の行列 A と B は類似した固有ベクトルを持っていますが、異なる固有値を持っています。
対角化不可能な行列
大部分の行列は複素数環境で対角化可能ですが、一部の行列は決して対角化できません。
この事実は、固有値 (または固有値) の代数的多重度が幾何学的多重度と一致しない場合に発生します。
たとえば、次の行列はいかなる方法でも対角化できず、「対角化可能」です。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}0&1 \\[1.1ex] 0&0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cdadeeadd8ee984e2efb53896c2d3306_l3.png)
さらに、実数環境では対角化できない行列もありますが、次の行列のように、複素数を扱う場合には対角化します。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}0&1 \\[1.1ex] -1&0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c7bb0fa6573d760edc55d94cfc834c7e_l3.png)
最後に、純粋に対角化可能ではなく、もう少し複雑な行列ブロック対角化手順がいくつかあります。最もよく知られている方法は、 Jordan の標準形式を使用した対角化です。
MATLAB で行列を対角化する
コンピューター プログラムは、特に行列が非常に大きい場合に、行列を対角化する場合に非常に便利です。最もよく知られているソフトウェアは間違いなくMATLABです。次に、このプログラムを使用して行列を対角的に因数分解する方法を見ていきます。
MATLAB で行列を対角化するために使用される命令は次のとおりです。
![]()
金
![]()
は対角化される行列であり、
![]()
そして
![]()
はプログラムが返す行列です。
![]()
は固有ベクトルによって形成される行列であり、
![]()
は、主な対角項が固有値である対角形式の行列です。
したがって、このコードをプログラムに入力するだけで済みます。
一方、固有値のみを知りたい場合は、次のステートメントを使用できます。
![]()
金
![]()
MATLAB が行列の固有値とともに返す列ベクトルです。
![]()
。