この記事では、完全な多項式とは何かを理解するために必要な概念を確認します。さらに、それがどのように使用されるか、そしてそれが多項式を操作および定量化する上でなぜそれほど重要なアイデアであるのかを学びます。ただし、まず最初に、多項式に関する記事を読むことを強くお勧めします。
完全多項式とは何ですか?
完全多項式は、項の和で構成される代数式です。各項は、係数と呼ばれる数値に x の累乗を乗算して形成されます。多項式の最高の累乗は多項式の次数と呼ばれ、最低の累乗 (x をゼロに累乗したもの) は独立項と呼ばれます。
ここから、完全な多項式を、多項式の次数までのすべての可能な次数の項を含むものとして定義します。つまり、多項式の次数が 5 の場合、次数 5、4、3、2、1、および 0 の項が含まれている必要があります。つまり、完全な多項式とは、ヌル項 (ゼロに等しい) を持たない多項式です。 )。
次の画像は、この例を示しています。見てわかるように、x の 4 乗 (4 は多項式の次数) から x の 0 乗まで、x の各指数に対する項が独立した項にあります。したがって、この多項式は完全な多項式の定義を満たします。
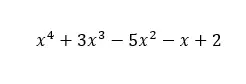
一方、次の画像のような別の多項式がある場合は、不完全な多項式を扱うことになります。 2 つの項が欠落しているため、x の項は 2 に引き上げられ、独立した項になります。そして、完全な多項式の定義から、1 つの項でも欠けている場合、その多項式は完全ではなくなります。
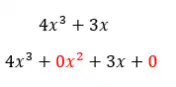
完全な多項式の例
完全な多項式の定義がわかったので、実際の例をいくつか見てみましょう。まず、次数 2 の完全な多項式、次数 4 の完全な多項式、最後に次数 6 の完全な多項式を見ていきます。明らかに、より高い次数の例を挙げることもできますが、考え方はすべてのタイプの多項式で同じです。
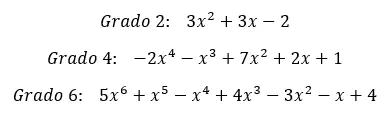
これらの例を使用すると、完全な多項式の定義が非常に明確になります。だからこそ私たちは次のレベルに進むことができるのです。次のセクションでは、存在する 2種類の完全多項式を項の順序に従って詳しく説明します。これは多くの学生にとって当たり前のことですが、改めて確認してみると良いでしょう。
完全多項式の種類
完全多項式は、順序付き完全多項式と順序なしまたは順序なしの完全多項式の 2 つのタイプに分類できます。 1 つ目は、項が x の次数に従って順序付けられる構造によって特徴付けられます。最上級の学位から始まり、独立という用語で終わります。
完全な順序のない多項式ですが、ランダムな順序の項で表現されます。したがって、独立項の次に最大の指数を持つ項を見つけることができます。ただし、この多項式の表現方法は実用的ではないため、常に順序付き多項式を使用することをお勧めします。
次に、それぞれのタイプの例を示します。これにより、違いがよくわかります。
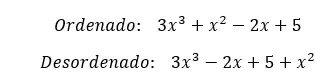
この記事が完全多項式の概念を理解するのに役立つことを願っています。ご質問がございましたら、お気軽にコメントに残してください。