多項式の根を計算するにはどうすればよいですか? (解けた演習)

このページでは、多項式の根とその計算方法について説明します。さらに、多項式の根を段階的に解く例や演習を見ることができます。

多項式の根は何ですか?

数学では、多項式の根 (またはゼロ) は、多項式を打ち消す値です。つまり、多項式の根は、多項式で評価されたときに 0 に等しい数値を持つすべての値です。

最終的に、

$x=a$

多項式の根です

$P(x)$

うん

$P(a)=0.$

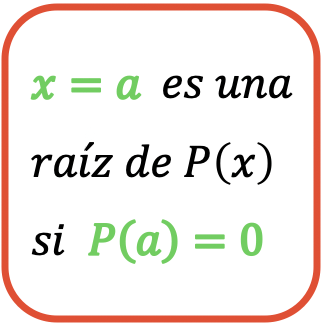
たとえば、次の多項式があるとします。

$P(x)=x^2-3x+2$

x=1における多項式の数値はゼロに等しいため、多項式の根の 1 つが 1 であることを確認できます。

$P(1)=1^2-3\cdot 1+2 = 1-3+2 \color{blue} \bm{= 0}$

一方、3 は多項式を打ち消す値ではないため、多項式の根ではありません。つまり、 x=3における多項式の数値はゼロとは異なります。

$P(3)=3^2-3\cdot 3+2 = 9-9+2=2 \color{blue} \bm{\neq 0}$

多項式の根が何であるかはよく理解できたと思いますが、多項式の根が何個あるか知りたくありませんか?あるいは、多項式の根をすべて見つけるにはどうすればよいでしょうか?そうですね、それはまさに次のセクションで見ていきます。

多項式のすべての根を計算するにはどうすればよいですか?

多項式の根をすべて見つけるには、次の手順に従う必要があります。

まず、多項式の独立項のすべての約数が計算されます。
次に、前のステップで見つかったすべての値が多項式で評価されます。
最後に、多項式内の数値を評価するときにその数値がゼロに等しい場合、その数値は多項式の根になります。それ以外の場合、その数は多項式の根に対応しません。

この手順は剰余定理から推定されます。この特定の手順の理由を確認するには、このリンクをクリックしてください。

多項式の根を計算する例

以下では、多項式の根を求める方法をよりよく理解できるように、例を段階的に解決していきます。

次の多項式の根はすべて何ですか?

$P(x) = x^2-5x+6$

まず第一に、独立項の約数を見つける必要があります。多項式のすべての根も独立項の約数になるからです。したがって、6 の約数は次のようになります。

6 の約数: +1、-1、+2、-2、+3、-3

数値が約数の場合、その負数も約数であることに注意してください。数値は正の数と負の数で割り切れるので。

したがって、多項式の可能な根またはゼロは、±1、±2、±3 になります。したがって、これらすべての値に対する多項式の数値を決定する必要があります。そして、これを行うために、これらの値を x がある多項式の式に代入します。

$P(1) = 1^2 -5\cdot 1 +6= 1 -5 +6 =2$

$P(-1) = (-1)^2 -5\cdot (-1) +6 =1+5+6 = 12$

$P(2) = 2^2 -5\cdot 2 +6 =4-10+6= \color{blue} \bm{0}$

$P(-2) = (-2)^2 -5\cdot (-2) +6 =4+10+6 =20$

$P(3) = 3^2 -5\cdot 3 +6 =9-15+6=\color{blue} \bm{0}$

$P(-3) = (-3)^2 -5\cdot (-3) +6 =9+15+6 =30$

したがって、多項式は変数xが +2 または +3 の場合にのみ消滅します。したがって、多項式の根は次のとおりです。

多項式の根またはゼロ: +2 および +3

一方、多項式には次数と同じ数の根があることに注意してください。つまり、多項式は 2 次であるため、根が 2 つあることになります。多項式の根の特性 (下記) で、この特性がどの多項式にも常に当てはまる理由がわかります。

多項式の根を求める方法を説明しました。ただし、これを達成する方法は他にもあります。たとえば、ルフィニの法則を使用して多項式の根を求めることもできます。次のリンクをクリックして、 Ruffini ルールの例を参照してください。ここでは、このよく知られたメソッドの構成と、2 つの手順の違いがわかります。

多項式の根の性質

多項式の根またはゼロには次の特性があります。

前に見たように、多項式の整数根 (またはゼロ) は、多項式の独立項の約数です。

多項式の根がすべてわかっている場合、その多項式を次のタイプの二項積の形で表現できます。
$(x-a).$

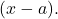
たとえば、多項式

$P(x) =x^3+3x^2-x-3$

それには3つの根があり、

$x=+1, x=-1$

そして

$x=-3.$

したがって、多項式を 3 つの因数の乗算の形式で書き直すことができます。各因数は変数によって形成されます。

$x$

そしてルートの符号が変わりました:

$\displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}$

$\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60}P(x) =x^3+3x^2-x-3 = (x\color{verd}\bm{-1}\color{black})\cdot (x\color{vermell}\bm{+1}\color{black}) \cdot (x\color{blau}\bm{+3}\color{black})$

これは多項式因数分解と呼ばれます。実際、多項式の根を求める主な用途の 1 つは、多項式を因数分解するために使用されることです。次のリンクでは、この非常に特殊な演算が何で構成されているかを確認でき、さらに、解かれた多項式因数分解演習で練習することができます。

多項式には、次数が示すのと同じ数の根があります。したがって、2 次多項式には 2 つの根があり、3 次多項式には 3 つの根があり、4 次多項式には 4 つの根があり、以下同様になります。

多項式に独立した項がない場合、その根の 1 つが 0 であることを意味します。その場合、残りの根は最低次数の単項式の係数の約数でなければなりません。

たとえば、次の多項式には独立項がありません。

$P(x) =x^3+x^2-2x$

したがって、多項式の 1 つの根は必ず 0 でなければなりません。そして、残りの根は最低次項の係数の約数、つまり -2 になります。より正確には、他のルートは次のとおりです。

$x=+1$

そして

$x=-2,$

したがって、多項式の根はすべて次のようになります。

多項式の根またはゼロ: 0、+1、および -2

多項式の根を決定できない場合、それは既約多項式であると言われます。

たとえば、次の多項式の根を計算してみます。

$P(x) =x^2+3x-1$

多項式の可能な根は、-1 の約数、つまり -1 と +1 だけです。したがって、多項式を次の値に評価します。

$P(1) = 1^2 +3\cdot 1 -1= 1 +3 -1 =3 \neq 0$

$P(-1) = (-1)^2 +3\cdot (-1)-1 =1-3-1 =-3 \neq 0$

どのような場合でも多項式はキャンセルされないため、根がなく、したがって既約多項式となります。

多項式が複数の多項式の積で構成されている場合、根を計算するためにこの積を行う必要はありませんが、多項式の根は乗算された各係数の根です。

たとえば、次の多項式があるとします。

$P(x) = (x-2) \cdot (x+1)$

多項式の根の 2 番目の特性から、左の多項式の根は +2、右の多項式の根は -1 であると推測できます。

$\displaystyle (x-2) \ \longrightarrow \ \text{ra\'iz} \ x=+2$

$\displaystyle (x+1) \ \longrightarrow \ \text{ra\'iz} \ x=-1$

したがって、2 つの因数の乗算から得られる多項式の根は、それぞれの根、つまり +2 と -1 になります。

$\displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}$

多項式の根に関する解決済み演習

演習 1

どうかを判断します

$x = -4$

は次の多項式の根です。

$P(x)=x^3+2x^2-11x-12$

解決策を見る

かどうかを確認するには

$x=-4$

は多項式の根なので、その値に評価する必要があります。まだ：

$\begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}$

の多項式の数値

$x=-4$

はゼロであるため、事実上多項式の根となります。

演習 2

次の多項式の根をすべて計算します。

$P(x)=x^2-3x+2$

解決策を見る

まず、多項式の可能な根を見つけるには、独立項の約数を見つける必要があります。したがって、2 の約数は次のようになります。

2 の約数: +1、-1、+2、-2

したがって、多項式の可能な根またはゼロは、±1 と ±2 です。したがって、これらすべての値で多項式がどの程度になるかを計算する必要があります。

$P(1)=1^2-3\cdot 1+2 =1-3+2=0$

$P(-1)=(-1)^2-3\cdot (-1)+2 =1+3+2=6$

$P(2)=2^2-3\cdot 2+2 =4-6+2=0$

$P(-2)=(-2)^2-3\cdot (-2)+2 =4+6+2=12$

したがって、 xが +1 または +2 の場合、多項式は消滅します。したがって、多項式の根は次のとおりです。

多項式の根またはゼロ: +1 および +2

演習 3

次の多項式の根を求めます。

$P(x)=x^3-x^2-4x+4$

解決策を見る

多項式の根も独立項の約数であるため、最初に独立項の約数を見つける必要があります。したがって、4 の約数は次のようになります。

4 の約数: +1、-1、+2、-2、+4、-4

したがって、多項式の可能な根またはゼロは、±1、±2、および ±4 になります。したがって、これらすべての値から多項式の数値を見つける必要があります。

$P(1)=1^3-1^2-4\cdot 1+4 =1-1-4+4=0$

$P(-1)=(-1)^3-(-1)^2-4\cdot (-1)+4 =-1-1+4+4=6$

$P(2)=2^3-2^2-4\cdot 2+4 =8-4-8+4=0$

$P(-2)=(-2)^3-(-2)^2-4\cdot (-2)+4 =-8-4+8+4=0$

$P(3)=3^3-3^2-4\cdot 3+4 =27-9-12+4=10$

$P(-3)=(-3)^3-(-3)^2-4\cdot (-3)+4 =-27-9+12+4=20$

したがって、多項式はxが +1、+2、または -2 の場合にのみ消滅するため、多項式の根は次のようになります。

多項式の根またはゼロ: +1、+2、および -2

演習 4

次の多項式の根を求めます。

$P(x)=x^3-6x^2+8x$

解決策を見る

この場合、多項式には独立した項がありません。したがって、上で説明した根の 4 番目の性質によれば、多項式の根の 1 つは 0 でなければならないことがわかります。

多項式の根:

$x=0$

さらに、この場合、考えられる根は独立項の約数ではなく、最下位項の係数の約数、つまり 8 です。

8 の約数: +1、-1、+2、-2、+4、-4、+8、-8

したがって、多項式の可能な根またはゼロは、±1、±2、±4、および ±8 です。したがって、これらすべての値で多項式の数値を計算する必要があります。

$P(1)=1^3-6\cdot 1^2+8\cdot 1 = 1-6+8=3$

$P(-1)=(-1)^3-6\cdot (-1)^2+8\cdot (-1) = -1-6-8=-15$

$P(2)=2^3-6\cdot 2^2+8\cdot 2 = 8-24+16=0$

$P(-2)=(-2)^3-6\cdot (-2)^2+8\cdot (-2) = -8-24-16=-48$

$P(4)=4^3-6\cdot 4^2+8\cdot 4 = 64-96+32=0$

$P(-4)=(-4)^3-6\cdot (-4)^2+8\cdot (-4) = -64-96-32=-192$

$P(8)=8^3-6\cdot 8^2+8\cdot 8 = 512-384+64=192$

$P(-8)=(-8)^3-6\cdot (-8)^2+8\cdot (-8) = -512-384-64=-960$

したがって、 x が+2 または +4 になると多項式が消えるので、これらの値が多項式の根になります。ただし、問題の最初に見つけたルート 0 も追加する必要があります。結論として、多項式の根はすべて次のようになります。

多項式の根またはゼロ: 0、+2、+4

演習 5

多項式の根のプロパティを使用して、次の多項式の根を計算します。

$P(x)=(x-1)(x+3)(x^2-x-2)$

解決策を見る

根の 6 番目の性質で見たように、多項式が因子の積によって形成される場合、多項式全体の根が各因子の根であるため、すべての根を計算する必要はありません。

さらに、多項式の根の 2 番目の特性から、最初の因子の根は +1 であり、2 番目の因子の根は -3 であると推定できます。

$\displaystyle (x-1) \ \longrightarrow \ \text{ra\'iz} \ x=+1$

$\displaystyle (x+3) \ \longrightarrow \ \text{ra\'iz} \ x=-3$

したがって、最後の要素の根を見つける必要があるだけです。これを行うには、独立項の約数 (-2) を求めます。

-2 の約数: +1、-1、+2、-2

したがって、最後の多項式の可能な根またはゼロは、±1 と ±2 です。これを使用して、これらすべての値における多項式の数値を計算する必要があります。

$q(x)= x^2-x-2$

$q(1)=1^2-1-2=1-1-2=-2$

$q(-1)=(-1)^2-(-1)-2=1+1-2=0$

$q(2)=2^2-2-2=4-2-2=0$

$q(-2)=(-2)^2-(-2)-2=4+2-2=4$

したがって、右側の多項式の根は -1 と 2 になります。

したがって、多項式全体の根は、見つかったすべての根になります。

多項式の根またはゼロ: +1、-1、+2、-3

多項式の根は何ですか?

多項式のすべての根を計算するにはどうすればよいですか?

多項式の根を計算する例

多項式の根の性質

多項式の根に関する解決済み演習

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする 返信をキャンセル

コメントする返信をキャンセル