▷ 多項式の乗算方法 (解決済み演習)

このページでは、多項式の乗算方法を学びます。多項式の乗算の例や、段階的に解決される演習も表示されます。最後に、乗算多項式の特性が何であるかを発見します。

ただし、多項式の乗算の概念を完全に理解するために、最も基本的なものから最も複雑なものに進みます。つまり、多項式に数値を乗算する方法から始めて、次に多項式に次の値を乗算する方法を見ていきます。単項式、そして最後に、2 つ以上の多項式を掛け合わせる方法を説明します。

この順序に従うことをお勧めしますが、前の多項式の演算をすでにマスターしていると思われる場合は、インデックスをクリックして多項式間の乗算に直接進むことができます。

多項式に数値を乗算します

スカラー (または数値) と多項式の積は非常に簡単に解くことができ、数値に多項式の各項の係数を乗算するだけです。

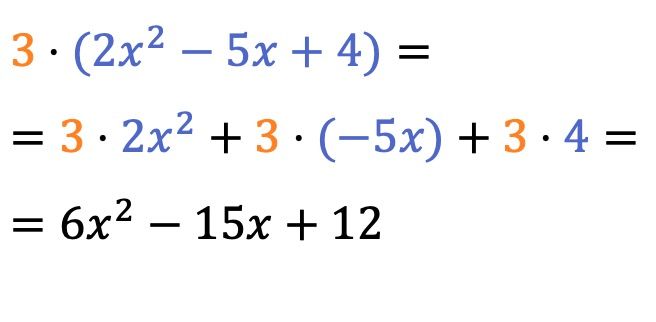
括弧の前の乗算記号は省略できます。

$\begin{array}{l} 2\cdot (5x^4-6x^2) = \\[2ex] =2 (5x^4-6x^2)= \\[2ex] = 10x^4-12x^2 \end{array}$

多項式と単項式の乗算

多項式と単項式の乗算方法を説明する前に、この種の多項式演算を実行するには単項式を知る必要があるため、まず単項式がどのように相互に乗算されるかを思い出してください。

2 つの単項式の積は、それぞれの係数を相互に乗算し、リテラル部分を相互に乗算することで構成されます。つまり、単項式の係数が乗算され、同じ基数を持つ変数の指数が加算されます。次の例を見てください。

$3x^2 \cdot 4x^5 = (3\cdot 4) x^{2+5} = 12x^7$

次に、単項式と多項式を乗算する方法を見てみましょう。

数学では、単項式と多項式の乗算を解くために、単項式に多項式の各項を乗算します。

前と同様に、乗算記号も省略できます。

$\begin{array}{l} -4x \cdot (2x^3-5x^2)= \\[2ex] =-4x (2x^3-5x^2)=\\[2ex] = -4x\cdot 2x^3 -4x \cdot (-5x^2) = \\[2ex] =-8x^4 +20x^3 \end{array}$

前の例では、単項式または多項式を乗算するときに、符号の規則も考慮する必要があることに注意してください。実際、単項式と多項式を乗算するときに非常によくある間違いは、項の符号を間違えることです。

確かに、ある時点で、数学で何か新しいものを見たとき、あなたは自問しました。それは何のためのものですか?このタイプの乗算は、多項式の共通因数を取得するために使用されます。これは、多項式を単純化できる操作です (非常に便利です)。このリンクでは、多項式の共通因数と多項式の共通因数の計算方法を確認できます。

2 つの多項式の乗算

多項式に数値と単項式を掛ける方法がわかったら、それが何なのか、そして多項式と多項式を掛ける方法を見てみましょう。

多項式を乗算するには、次の手順に従います。

最初の多項式の各項と 2 番目の多項式のすべての項を乗算します。
同じ次数の単項式 (類似した単項式) を加算 (または減算) します。

この方法が何であるかを正確に理解できるように、次の多項式の乗算を段階的に解決していきます。

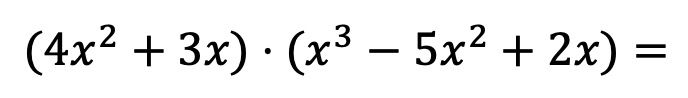
まず最初に、最初の乗算多項式の各要素を 2 番目の多項式の各項で乗算する必要があります。

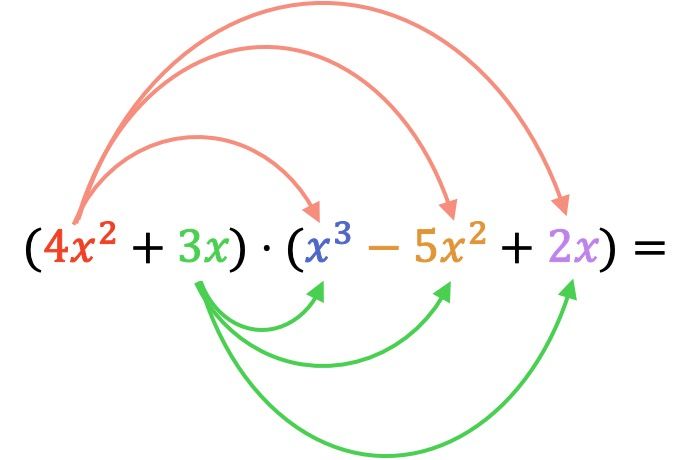
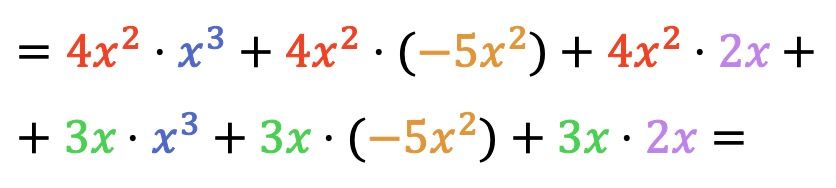
ここで、単項式のすべての乗算を実行します。

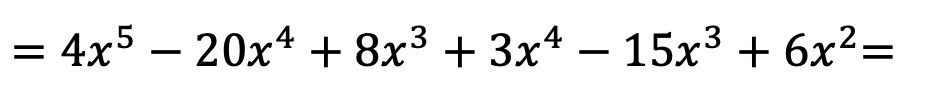
多項式を掛け合わせたら、結果の類似した項、つまり同じ文字と同じ指数を持つ項をグループ化するだけです。

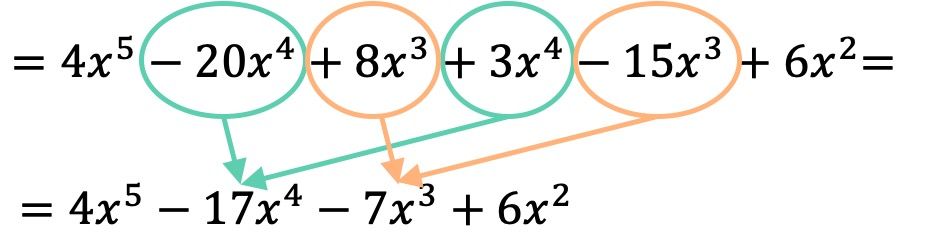
したがって、多項式乗算の結果は次のようになります。

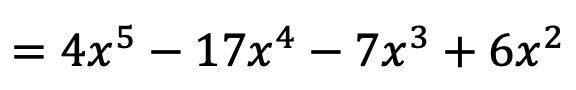
このようにして、多項式の乗算をすでに計算しています。もしかしたら、今はとても難しいように思えるかもしれませんが、2 つまたは 3 つの演習で練習すると、はるかに簡単になることがわかります。

2 つの多項式間の乗算がどのように解かれるかを理解できたので、おそらく多項式の除算方法を知りたいと思われるでしょう。実際、多項式の除算は乗算よりもはるかに複雑です。そのため、完全に理解できるように手順 (およびヒント😉) を段階的に説明しました。興味があれば、このリンクをクリックして、多項式がどのように分割されるかを確認してください。

垂直多項式乗算

多項式と別の多項式を水平方向に乗算する方法を説明しましたが、これは、多項式を垂直方向に乗算するという、より古典的な方法でも行うことができます。多項式乗算の例を解いて、この方法がどのように使用されるかを見てみましょう。

次の 2 つの多項式を垂直方向に乗算する場合:

$(5x^2+3x-4) \cdot (2x^2-x)$

最初に行う必要があるのは、多項式の代数乗算として、一方の多項式を他方の下に配置することです。

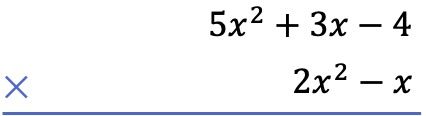
次に、以下の多項式の各項と上の多項式の各項を乗算し、その結果を最高次数から最低次数まで列ごとに並べます。

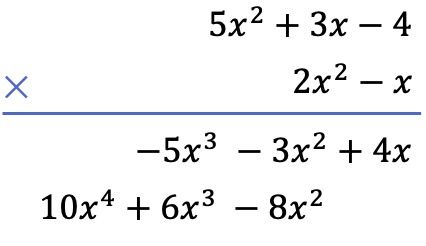
最後に、垂直方向に整列した項を追加します。

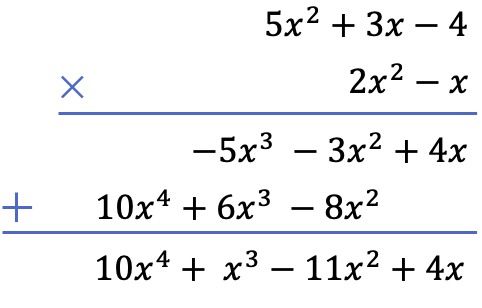
多項式の乗算を解くために存在する 2 つの方法を見てきましたが、分数と多項式の乗算もできることをご存知ですか?これらの種類の分数を使用すると、乗算だけでなくあらゆる種類の演算を実行できます。このリンクをクリックして、 代数分数とは何かを調べてください。

多項式乗算の性質

多項式の乗算には次の特徴があります。

可換性の性質: 乗算多項式の次数は乗算の結果を変更しません。

$P(x)\cdot Q(x) = Q(x) \cdot P(x)$

結合特性: 3 つ以上の多項式を乗算すると、因子がどのようにグループ化されているかに関係なく、積の結果は同じになります。

$\bigl(P(x) \cdot Q(x)\bigr) \cdot R(x) =P(x) \cdot \bigl(Q(x) \cdot R(x)\bigr)$

分配特性: 2 つの多項式の合計に 3 番目の多項式を乗算した値は、各加算の合計に 3 番目の多項式を乗算した値に等しくなります。

$P(x)\cdot \bigl(Q(x)+ R(x)\bigr) = P(x)\cdot Q(x) + P(x) \cdot R(x)$

2 つの多項式間の乗算から得られる多項式の次数は、乗算された 2 つの多項式の次数の合計に等しくなります。

多項式の乗算に関する演習を解決しました

練習できるように、多項式の乗算に関する解決済みの演習をいくつか残しておきます。自分で問題を解決してみて、提案された解決策で結果を確認することができます。コメントでご質問いただければ、喜んでお手伝いさせていただきます。

演習 1

多項式とスカラー間の次の積を計算します。

$\text{A)} \ 4\cdot (2x^3-4x)$

$\text{B)} \ -3 \cdot (-5x^2+9x)$

$\text{C)} \ 5\cdot(3x^2+4x-7)$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7)$

解決策を見る

多項式と数値の乗算を計算するには、数値に多項式の各要素の係数を乗算する必要があります。それで：

$\text{A)} \ 4\cdot (2x^3-4x) =4 \cdot 2x^3 -4\cdot 4x = \bm{8x^3-16x}$

$\text{B)} \ -3 \cdot (-5x^2+9x) = -3 \cdot (-5x^2)-3\cdot 9x = \bm{15x^2-27x}$

$\text{C)} \ 5\cdot(3x^2+4x-7) = \bm{15x^2+20x-35}$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7) = \bm{-24x^5+36x^3-48x^2+42}$

演習 2

多項式と単項式の間の次の乗算を解きます。

$\text{A)} \ 2x \cdot (5x^2+3)$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5)$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x)$

解決策を見る

多項式と単項式の乗算を解くには、その単項式に多項式の各項を乗算する必要があります。それで：

$\text{A)} \ 2x \cdot (5x^2+3) = 2x \cdot 5x^2+2x\cdot 3 = \bm{10x^3+6x}$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)= -4x^2 \cdot 6x^4 - 4x^2 \cdot (-9x^2) = \bm{-24x^6+36x^4}$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5) = \bm{10x^6-10x^5+25x^3}$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x) = \bm{21x^8-12x^7-3x^5-9x^3}$

演習 3

次の多項式間の乗算の結果を求めます。

$\text{A)} \ (4x^2 + 1) \cdot (3x^2-2)$

$\text{B)} \ (-3x^4+2x) \cdot (5x^4-x)$

$\text{C)} \ (2x^3-5x^2)\cdot (4x-7)$

解決策を見る

2 つの多項式の乗算を計算するには、最初の多項式の各要素と 2 番目の多項式の各要素を乗算し、類似した項をグループ化する必要があります。それで：

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2 + 1) \cdot (3x^2-2) = \\[2ex] =4x^2 \cdot 3x^2 +4x^2\cdot (-2) +1 \cdot 3x^2 +1 \cdot (-2) = \\[2ex] = 12x^4-8x^2+3x^2 -2 = \\[2ex] = \bm{12x^4-5x^2-2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (-3x^4+2x) \cdot (5x^4-x) = \\[2ex] =-3x^4\cdot 5x^4 -3x^4\cdot (-x) +2x \cdot 5x^4 +2x \cdot (-x) = \\[2ex] = -15x^8+3x^5+10x^5-2x^2 = \\[2ex] = \bm{-15x^8+13x^5-2x^2} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^3-5x^2)\cdot (4x-7) = \\[2ex] =2x^3\cdot 4x +2x^3\cdot (-7) -5x^2 \cdot 4x -5x^2\cdot (-7) = \\[2ex] = 8x^4-14x^3-20x^3+35x^2 = \\[2ex] = \bm{8x^4-34x^3+35x^2} \end{array}$

演習 4

次の多項式間の乗算の結果を求めます。

$\text{A)} \ (4x^2-6x+2) \cdot (5x^3-x^2)$

$\text{B)} \ (3x^3-2x+7) \cdot (-4x^3+5x)$

$\text{C)} \ (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3)$

解決策を見る

2 つの多項式の乗算を計算するには、最初の多項式の各要素と 2 番目の多項式の各要素を乗算し、同様の項を加算する必要があります。それで：

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2-6x+2) \cdot (5x^3-x^2) = \\[2ex] =4x^2 \cdot 5x^3 +4x^2\cdot (-x^2) -6x \cdot 5x^3 -6x \cdot (-x^2) + 2 \cdot 5x^3 +2 \cdot (-x^2) = \\[2ex] = 20x^5-4x^4-30x^4+6x^3+10x^3-2x^2 = \\[2ex] = \bm{20x^5-34x^4+16x^3-2x^2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (3x^3-2x+7) \cdot (-4x^3+5x) = \\[2ex] =3x^3 \cdot (-4x^3) +3x^3\cdot 5x -2x \cdot (-4x^3) -2x \cdot 5x + 7 \cdot (-4x^3) +7 \cdot 5x = \\[2ex] =-12x^6+15x^4+8x^4-10x^2-28x^3+35x = \\[2ex] = \bm{-12x^6+23x^4-28x^3-10x^2+35x} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3) = \\[2ex] = 18x^9-36x^8-45x^7-8x^8+16x^7+20x^6+2x^7-4x^6-5x^5 = \\[2ex] = \bm{18x^9-44x^8-27x^7+16x^6-5x^5} \end{array}$

演習 5

次の多項式の乗算を計算します。

$\text{A)} \ (2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)$

$\text{B)} \ (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)$

$\text{C)} \ (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8)$

解決策を見る

2 つの多項式の積を作成するには、最初の多項式の各項と 2 番目の多項式の各項を乗算し、得られた類似の単項式をグループ化する必要があります。まだ：

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l}(2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)= \\[2ex] = 8x^6-12x^5+12x^5-18x^4-24x^4+36x^3+20x^3-30x^2-4x^2+6x = \\[2ex] = \bm{8x^6-42x^4+56x^3-34x^2+6x} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)= \\[2ex] =-x^5-5x^4+2x^3+9x^2+4x^4+20x^3-8x^2-36x-7x^3-35x^2+14x+63 = \\[2ex] = \bm{-x^5-x^4+15x^3-34x^2-22x+63} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8) = \\[2ex] = 8x^{13}-16x^{10}-2x^9+16x^7+24x^{11}-48x^8-6x^7+48x^5+ \\[2ex] + \ 12x^{10}-24x^7-3x^6+24x^4-20x^8+40x^5+5x^4-40x^2 = \\[2ex] = \bm{8x^{13}+24x^{11}-4x^{10}-2x^9-68x^8-14x^7-3x^6+} \\[2ex] \bm{+ \ 88x^5+29x^4-40x^2} \end{array}$

演習 6

次の 3 つの多項式の乗算を解きます。

$(2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x)$

解決策を見る

この問題の演算は 2 つの多項式の乗算で構成され、より正確には 2 つの二項式と 1 つの三項式で構成されます。したがって、最初に積を求めてから、その結果に残りの多項式を乗算する必要があります。

したがって、最初の乗算を計算します。

$\begin{array}{l} (2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x) = \\[2ex] = \bigl[-10x^6+6x^4-12x^2+15x^4-9x^2+18 \bigr]\cdot (9x^3-6x) = \\[2ex] = (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)\end{array}$

そして残りの乗算を解きます。

$\begin{array}{l} (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)= \\[2ex] = -90x^9+60x^7+189x^7-126x^5-189x^5+126x^3+162x^3-108x \\[2ex] =\bm{-90x^9+249x^7-315x^5+288x^3-108x} \end{array}$

演習 7

次の多項式に有理係数 (分数を含む) を掛けます。

$\displaystyle \left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right)$

解決策を見る

多項式には分数がありますが、それでも 2 つの多項式間の乗算です。したがって、これは他の多項式の積と同じように解く必要があります。つまり、すべての要素を掛け合わせてから、類似した単項式をグループ化します。

したがって、多項式を乗算します。

$\displaystyle \begin{array}{l} \displaystyle\left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right) = \\[4ex] = \displaystyle\frac{1}{3}x^2 \cdot 5x +\frac{1}{3}x^2\cdot \left(- \frac{2}{7} \right) -4x \cdot 5x - 4x \cdot \left(- \frac{2}{7} \right) = \\[4ex] =\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x\end{array}$

そして最後に、リテラル部分が同一である用語を追加 (または減算) します。

$\begin{array}{l}\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x= \\[4ex] \displaystyle= \frac{5}{3}x^3 -\frac{2}{21}x^2 -\frac{420}{21}x^2+\frac{8}{7} x \\[4ex] \displaystyle=\mathbf{\frac{5}{3}}\bm{x^3} -\mathbf{\frac{422}{20}}\bm{x^2}+\mathbf{\frac{8}{7}} \bm{x} \end{array}$

この演習を正常に完了するには、分数の演算をマスターすることが重要です。ただし、各ステップについてご質問がある場合は、コメント欄で質問していただければ、できるだけ早くお答えいたします。

多項式の乗算 (または積)

多項式に数値を乗算します

多項式と単項式の乗算

2 つの多項式の乗算

垂直多項式乗算

多項式乗算の性質

多項式の乗算に関する演習を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

演習 6

演習 7

コメントする返信をキャンセル

多項式に数値を乗算します

多項式と単項式の乗算

2 つの多項式の乗算

垂直多項式乗算

多項式乗算の性質

多項式の乗算に関する演習を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

演習 6

演習 7

コメントする 返信をキャンセル

コメントする返信をキャンセル