この記事では、関数の単調性を知る方法、つまり関数の増加と減少の間隔を求める方法を説明します。さらに、機能の成長と低下に関する段階的な演習を行うことができます。
関数の単調性とは何ですか?
関数は、指定された順序を維持する場合、ある区間で単調になります。単調さには 5 つのタイプがあります。
- 単調増加関数:ある点での関数の値が常に前の点での関数の値以上である場合。
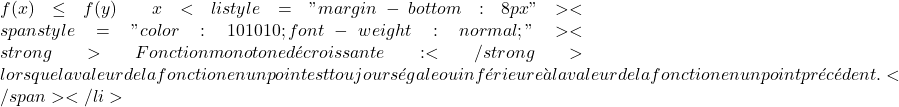厳密に単調増加する関数:ある点での関数の値が、常に前の点での関数の値よりも大きい場合。
ある時点での関数の値が、前の時点での関数の値と常に等しい場合の定数関数。
x^2-4=0x^2=4x=\pm 2
\text{Dom } f= \mathbb{R}-\{+2, -2 \}
f(x)=\cfrac{3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-4) – 3\cdot 2x}{\left( x^2-4\right)^2}f'(x)=\cfrac{-6x}{\left(x^2-4\right)^2}
f'(x)=0\cfrac{-6x}{\left(x^2-4\right)^2}=0
\left(x^2-4\right)^2}
-6x=0\cdot \left(x^2-4\right)^2-6x=0x=\cfrac{0}{-6}x=0
f'(x)=0、
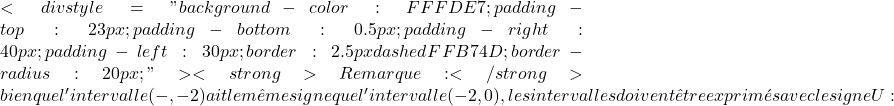
(-\infty,0)
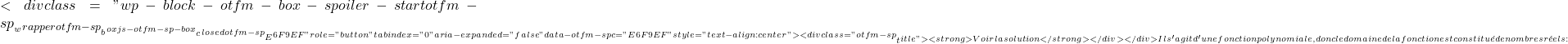
f'(x)=0。
f(x)=x^3-6x^2+9x \ \longrightarrow \ f'(x)=3x^2-12x+9
f'(x)= 03x^2-12x+9=0\begin{aligned}x &=\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} = \cfrac{-(- 12) \pm \sqrt{(-12)^2-4\cdot 3 \cdot 9}}{2\cdot 3}=\\[2ex]&= \cfrac{+12 \pm \sqrt{144-108 }}{6} =\cfrac{12 \pm 6}{6}=\begin{ケース} \cfrac{12 + 6}{6}= 3 \\[4ex] \cfrac{12 – 6}{6} =1 \end{ケース} \end{整列}
f'(x)=0
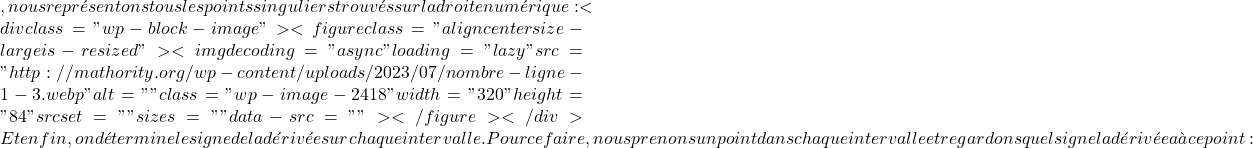
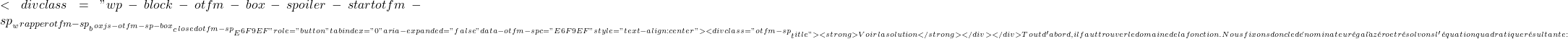
\text{Dom } f= \mathbb{R}-\{+3, -3 \}
f(x)=\cfrac{5}{x^2-9} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-9) – 5\cdot (2x)}{\ left(x^2-9\right)^2}f'(x)= \cfrac{-10x}{\left(x^2-9\right)^2}
f'(x)= 0\cfrac{-10x}{\left(x^2-9\right)^2}=0 -10x=0\cdot \left(x^2-9\right)^2 – 10x= 0 x= \cfrac{0}{-10} x=0
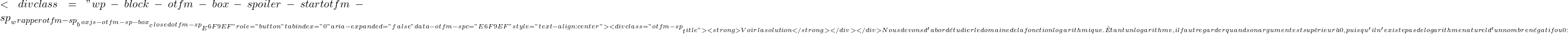
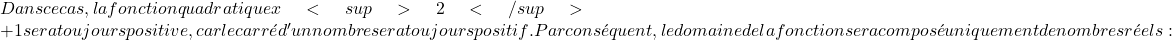
f(x)=\ln \bigl(x^2+1 \bigr) \ \longrightarrow \ f'(x)=\cfrac{1}{x^2+1 } \cdot (2x)f'(x) = \cfrac{2x}{x^2+1}
f'(x)= 0\cfrac{2x}{x^2+1}=0 2x=0\cdot \left(x^2+1\right) 2x= 0 x= \cfrac{0}{2} x=0
