垂直面

このページでは、垂直面とは何か、2 つの面が垂直であるかどうかを判断する方法、垂直面を計算する方法、垂直面の例と解答済みの演習を説明します。

2 つの垂直な平面とは何ですか?

解析幾何学では、2 つの平面が直角 (90 度) で交差する場合、それらの平面は垂直になります。

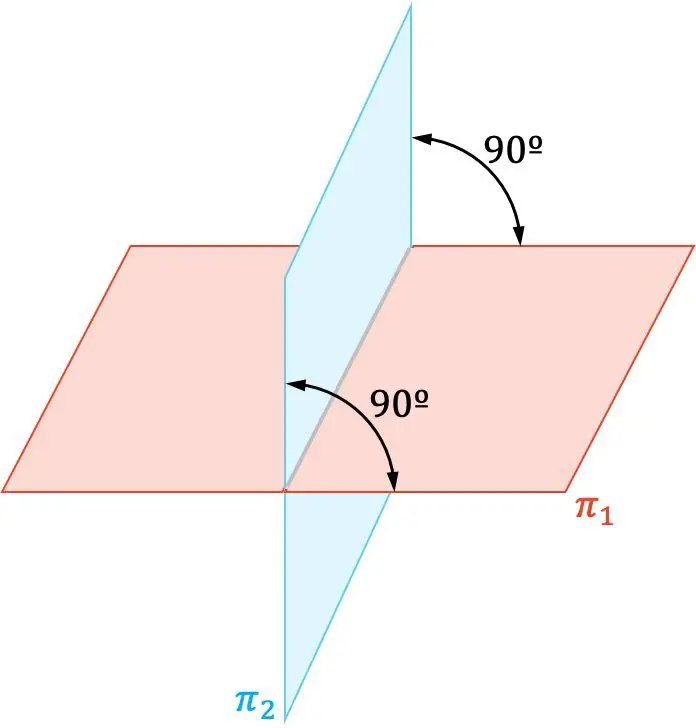
また、垂直な２つの面の法線ベクトルも互いに直交している。

明らかに、2 つの垂直面は線で交差するため、間の距離は常にゼロです。非常に単純なように見えますが、 2 つの平面間の距離の概念は非常に重要なので、質問がある場合はリンクにアクセスすることをお勧めします。

一方、空間 (R3) 内の 2 つの平面は交差したり、平行したり、一致したりする可能性があるため、垂直に配置された 2 つの平面が平面間の唯一の可能な相対位置ではありません。

ある平面が別の平面に垂直かどうかはどうやってわかりますか?

垂直面の定義を理解したら、2 つの面が垂直かどうかを確認する方法を見てみましょう。

2 つの平面は、その法線ベクトルが垂直である場合に垂直になります。したがって、2 つの平面が互いに垂直であるかどうかを判断するには、それらの法線ベクトルによって形成される角度を計算する必要があります。これらの平面が 90 度の角度を形成する場合、これは平面が垂直であることを意味します。

したがって、2 つの平面の垂直度を見つけるには、2 つのベクトル間の角度を計算する方法を知る必要があります。その方法を覚えていない場合は、リンクを参照してください。そこには、説明と 2 つのベクトルの間の角度を決定するために必要な公式が記載されています。さらに、例題を見て、解決された演習で練習することができます。

しかし、簡単に言うと、2 つのベクトルは、その内積が 0 の場合、垂直になります。したがって、2 つの平面は、それらに関連付けられた法線ベクトルの内積が 0 の場合に垂直になります。

2 つの垂直な平面の例

たとえば、次の 2 つの平面が垂直であるかどうかを確認してみましょう。

平面に垂直なベクトルの座標 X、Y、Z は、その一般 (または暗黙の) 方程式の係数 A、B、C と一致します。したがって、各平面の法線ベクトルは次のようになります。

そして、法線ベクトル間の内積を計算することで、これらが 2 つの垂直面であるかどうかを確認します。

2 つの法線ベクトル間の内積は 0 であるため、 2 つの平面は互いに垂直です。

点における線に垂直な平面を計算します

典型的な平面と直線の問題は、特定の点における直線に垂直な平面の方程式を見つけることです。そこで、次に例を使ってそれがどのように解決されるかを見ていきます。

• 直線に垂直な平面の方程式を求めます。

  

  について

  

  ストレートに言われて指摘する：

まず、問題の平面に垂直なベクトルを見つける必要があります。そして直線のように

が平面に垂直である場合、その法線ベクトルは線の方向ベクトルと一致します。

この場合、行は

はパラメトリック方程式の形式であるため、その方向ベクトルの成分はパラメータの前の項になります。

したがって、平面に垂直なベクトルは、線の方向ベクトルと同じになります。

したがって、計画の暗黙的な (または一般的な) 方程式は次のようになります。

したがって、係数 D の値を決定するだけで十分です。これを行うには、その点が平面に属していることがわかる点の座標を方程式に代入します。

つまり、平面のデカルト方程式は次のようになります。

一方、幾何学的オブジェクト間の垂直性についてさらに練習したい場合は、垂直線に関するページにアクセスしてください。 2 本の線が直交する場合、一方の線ともう一方の線の垂直を計算する方法、例、解決された演習など、垂直線について知っておくべきすべてのことが見つかります。

垂直面の性質

すべての垂直面には次の特性があります。

• 対称関係: ある平面が別の平面に垂直な場合、この平面も最初の平面に対して垂直になります。この性質は平行面でも保持されます。

• 非反射特性: 明らかに、それ自体に対して垂直になる平面は存在しません。

• 定理: 3 次元 (3D) 空間では、3 番目の平面に垂直な平面のペアは必ず平行でなければなりません。言い換えれば、ある平面が別の平面に垂直であり、この平面が 3 番目の平面にも垂直である場合、最初と最後の平面は互いに平行です。