ここでは、関数の双曲線逆正割関数の導関数を計算する方法を説明します。さらに、双曲逆正割関数の導関数の解決例も表示されます。
双曲線逆正割微分公式
x の双曲線逆正割の導関数は、x の積で 1 の平方根を引いた値で割ったマイナス 1 に等しくなります。
![]()
したがって、関数の双曲線アークセカントの微分値は、その関数の微分値を、関数の積と 1 の根から 2 乗関数を引いた値で割った値を引いたものになります。
![]()
つまり、双曲線逆正割関数の導関数の公式は次のとおりです。
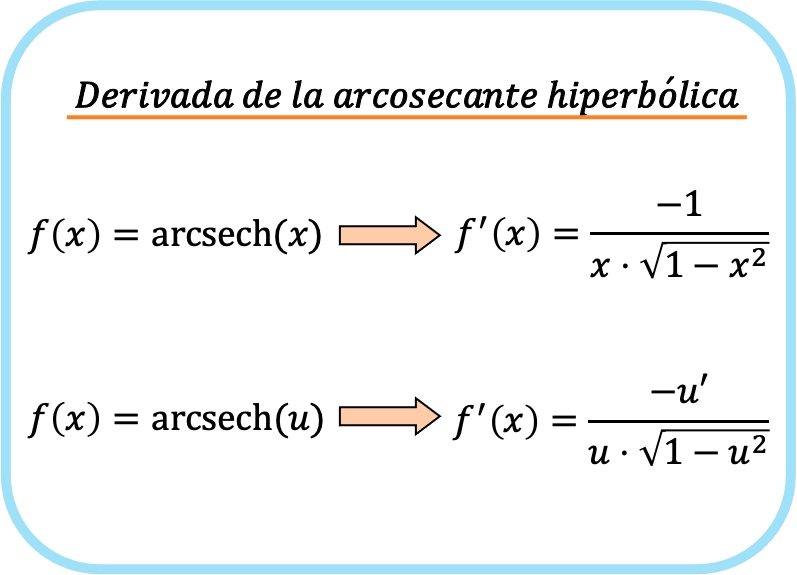
両方の式は実際には同じ式に対応しますが、2 番目の式には連鎖規則が適用されます。実際、恒等関数 x を u に置き換えると、x の導関数は 1 であるため、最初の式が得られます。
双曲逆正割関数の導関数の例
双曲線アークセカントの導関数の公式が何であるかを確認した後、このタイプの逆三角関数導関数の 2 つの段階的な演習を解いていきます。したがって、関数の双曲線逆正割を導出する方法を正確に理解できます。
例1
この例では、2x 双曲線アークセカントの導関数が何であるかを決定します。
![]()
双曲逆正割引数には x 以外の関数があるため、それを導出するには連鎖規則の公式を使用する必要があります。
![]()
関数 2x は線形なので、導関数は 2 です。したがって、導関数を求めるには、単純に u に 2x を、u’ に 2 を式に代入します。
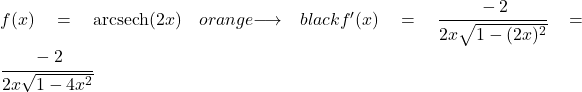
例 2
この 2 番目の演習では、多項式関数の双曲線逆正割を導出します。
![]()
双曲逆正割関数には引数に別の関数があるため、この演習の関数は複合的です。したがって、双曲線アークセカントの導関数公式を連鎖規則とともに使用して、その導出を行う必要があります。
![]()
したがって、分数の分子には引数の多項式関数の導関数を入れ、分母には多項式関数によって u を変更します。
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arcsech}(x^3-4x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(3x^2-4)}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\\[1.5ex] &=\cfrac{-3x^2+4}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f6389de5c7761fb5d35a9861156eec1_l3.png)