双曲線正接関数

このページには、双曲線正接に関するすべてが記載されています。その式、グラフ表現、そのすべての特性など。

双曲線正接の公式

双曲線正接関数は主要な双曲線関数の 1 つであり、記号Tanh(x)で表されます。数学的には、双曲線正接は双曲線正弦を双曲線余弦で割ったものに等しくなります。

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

双曲線サインの公式と双曲線コサインの公式から、次の式に到達できます。

$\text{tanh}(x)=\cfrac{e^x-e^{-x}}{e^x+e^{-x}}$

したがって、双曲線正接関数は指数関数に関連します。次のリンクでは、これらのタイプの関数のすべての特性を確認できます。

➤参照:指数関数の特性

双曲線正接のグラフ表示

その式から、双曲線正接関数をグラフで表すことができます。

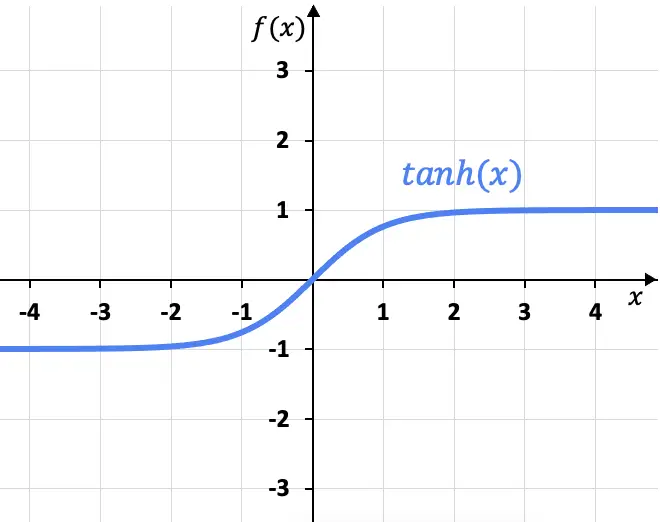
グラフからわかるように、双曲線正接関数には x=+1 と x=-1 に 2 つの水平漸近線があります。これは、x がプラスの無限大に近づくと関数の極限が x=+1 となり、マイナスの無限大に近づくと関数の極限が得られるためです。 x=-1を与えます。

一方、双曲線正接のグラフは、周期関数であるタンジェント（三角関数）のグラフとは何の関係もありません。次のリンクで、タンジェントのグラフィック表示と、それが双曲線タンジェントとどのように異なるかを確認できます。

➤参照:正接関数のグラフ表示

双曲線正接の特徴

双曲線正接関数には次の特性があります。

双曲線正接関数の定義域はすべて実数です。

$\text{Dom } f = \mathbb{R}$

対照的に、双曲線正接関数のパスまたは範囲は、-1 から +1 までの値に制限されます (両端を含みません)。

$\text{Im } f= (-1,1)$

双曲線正接は、連続、全単射、奇関数 (座標の原点に関して対称) です。

$\displaystyle \text{tanh}(-x) =- \text{tanh}(x)$

この関数は、座標原点で X 軸と Y 軸と交差します。

$(0,0)$

双曲線正接関数のプラス/マイナス無限大の制限は +1/-1 を与えます。したがって、関数には x=+1 に水平漸近線があり、x=-1 に別の水平漸近線があります。

$\displaystyle\lim_{x\to+\infty}\text{tanh}(x)=+1$

$\displaystyle\lim_{x\to-\infty}\text{tanh}(x)=-1$

双曲線正接はその領域全体にわたって厳密に増加しているため、相対的な極値 (最大値も最小値も) がありません。

ただし、関数は点 x = 0 で凸から凹に変化するため、x = 0 は関数の変曲点になります。

双曲線正接関数の逆関数は、双曲線正接 (または双曲線逆正接) 引数と呼ばれ、その式は次のとおりです。

$\displaystyle\text{tanh}^{-1}(x)=\text{arg tanh}(x)=\cfrac{1}{2}\ln\left(\frac{1+x}{1-x}\right)$

双曲線正接関数の導関数は、1 を双曲線余弦の 2 乗で割ったものです。

$f(x)=\text{tanh}(x) \ \longrightarrow \ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=1-\text{tanh}^2(x)$

双曲線正接関数の積分は、双曲線余弦の自然対数です。

$\displaystyle\int\text{tanh}(x) \ dx= \ln\Bigl(\text{cosh}(x)\Bigr)+C$

2 つの異なる数値の合計の双曲線正接は、次の方程式を適用することで計算できます。

$\text{tanh}(x+y)=\cfrac{\text{tanh}(x)+\text{tanh}(y)}{1+\text{tanh}(x)\cdot \text{tanh}(y)}$

テイラー多項式または双曲線正接系列には収束半径があります
$\left|x\right|<\cfrac{\pi}{2}$

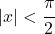
これは次の式に相当します。

$\displaystyle\text{tanh}(x)=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\cdots =\sum_{n=1}^\infty\frac{2^{2n}(2^{2n}-1)B_{2n} x^{2n-1}}{(2n)!}$

金

$B_n$

はベルヌーイ数です。

双曲線正接の公式

双曲線正接のグラフ表示

双曲線正接の特徴

コメントする 返信をキャンセル

コメントする返信をキャンセル