このページでは、常方程式、一般方程式、その他の種類の円周方程式、円周方程式が正しい場合など、円周方程式に関するすべての情報が見つかります。さらに、方程式を見つける方法の例も表示されます。円周の分、解いた練習問題で練習することができます。
円の常方程式
円周方程式が何であるかを理解する前に、円周の概念を思い出してください。
円周とは、中心と呼ばれる固定点から等距離にある平面上の点の軌跡です。

したがって、円上のすべての点はその中心からの距離が同じになります。
さらに、円は、楕円、放物線、双曲線と並ぶ 4 つの円錐断面の 1 つです。つまり、円錐を底面に平行な面で切ると円が得られます。
デカルト平面内の円を記述する最も簡単な方法は、その常方程式を使用することです。したがって、円周の常方程式の公式は次のようになります。
円の常方程式は次のとおりです。
![]()
金:
-

円の半径です。
-

そして

は円の中心の座標です。
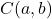
ちょっと面倒なので説明はしませんが、この方程式はピタゴラスの定理から求めることができます。
例を使用して、円の常方程式がどのように計算されるかを見てみましょう。
- 点を中心とする半径5の円の常方程式を求めます。
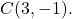
円の常方程式の公式は次のとおりです。
![]()
したがって、未知のものを置き換えるだけで済みます
![]()
半径の値と未知数による
![]()
そして
![]()
円の中心の座標 X と Y によってそれぞれ次のように計算されます。
![]()
したがって、円の常方程式は次のようになります。
![]()
円の一般方程式
別のタイプの円周方程式は一般方程式であり、実際、これが最もよく使用されます。次に、常方程式から任意の円周の一般方程式を取得する方法を見ていきます。
円の常方程式を考えてみましょう。
![]()
私たちが驚くべき同等性 (または驚くべき製品) を開発した場合:
![]()
![]()
ここで、変数を 3 つ変更します。
![]()
そして最後に、円周の一般方程式を取得します。
![]()
したがって、円周の一般方程式の公式は次のようになります。
![]()
ここで、円の中心は次のとおりです。
![]()
そして、円の半径は次のようになります。
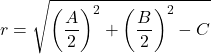
したがって、この円周方程式は常に常方程式によって得られます。これがどのように行われるかを示す例を次に示します。
- 点を中心とする半径6の円の一般方程式を求めます。
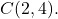
まず、円の常方程式を見つける必要があります。これを行うには、彼の公式を使用します。
![]()
![]()
そして円周の一般方程式が見つかるまで、つまり単純化できなくなるまで操作を続けます。
![]()
![]()
![]()
![]()
したがって、円の一般方程式は次のようになります。
![]()
この問題では必要ありませんでしたが、見つかった方程式の中心と半径を計算して、それが正しいことを確認できます。
円の中心を決定するには、次の式を使用します。
![]()
![]()
![]()
![]()
実際、円の中心はステートメントの中心と一致します。
また、次の式で円周の半径も確認します。
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04dc99d462a8ceb5e6dca936999a4ce8_l3.png)
また、半径もステートメントの半径と等しくなります。したがって、計算された円周方程式は正しいです。
円周の存在
次の形式のすべての方程式
![]()
円に相当します。したがって、このタイプの式が真に円の方程式であるためには、次の 3 つの条件が満たされる必要があります。
- の係数
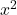
そしての
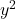
それらは 1 に等しくなければなりません。両方の変数の前に 1 以外の数字が付いているが、両方とも同じ数字である場合、方程式全体がその数字で除算され、係数が 1 になる可能性があることに注意してください。
- 方程式に項を含めることはできません
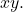
- 次の式は正の値である必要があります。
 他の種類の円方程式
他の種類の円方程式
これまで見てきた 2 つの円方程式、常方程式と一般方程式は、平面 (R2) 内で円を数学的に表現するために最もよく使用されます。ただし、この幾何学的オブジェクトを説明するには数種類の方程式があり、以下にそれぞれについて説明します。
円の正準方程式
円の正準方程式、または縮小方程式は、中心が座標の原点、つまり点 (0,0) にある円を記述するために使用されます。この方程式は次のとおりです。
![]()
さらに、半径が単位 (1) と等しい場合、円周の方程式は次のようになります。
![]()
この最後の方程式は、単位円周または単位円とも呼ばれるゴニオメトリック円周に対応します。座標原点を中心とした半径1の円です。
2つの同心円の方程式
2 つの同心円方程式は、中心が同じ点にある方程式です。 2 つの同心円の唯一の違いは半径です。
したがって、この条件が満たされるためには、 2 つの同心円の方程式は、独立項を除いてまったく同じであり、独立項は異なっていなければなりません。
![]()
![]()
たとえば、次の 2 つの円は、独立した項を除いてすべての係数が同一であるため、同心円です。
![]()
![]()
円のパラメトリック方程式
直線と同様に、円の方程式もサインとコサインの三角関数でパラメータ化できます。したがって、円のパラメトリック方程式は次のようになります。
![Rendered by QuickLaTeX.com \diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)](https://mathority.org/wp-content/ql-cache/quicklatex.com-72dae5b3c5f775661ecb102945bb3fbd_l3.png)
どこがポイントですか
![]()
は円の中心であり、
![]()
ここはあなたの部署です。
円の方程式の問題を解きました
演習 1
点を中心とする半径5の円の一般方程式を計算します。
![]()
円の一般方程式を見つけるには、まずその常方程式を見つける必要があります。これを行うには、円の常方程式の公式を使用します。
![]()
![]()
![]()
常方程式がわかったら、円の一般方程式が見つかるまで作業を進めます。
![]()
![]()
![]()
![]()
したがって、円の一般方程式は次のようになります。
![]()
演習 2
次の各円について、その中心の座標と半径の長さを見つけます。
![]()
![]()
![]()
円周A)
![]()
円周は常方程式の形式で表され、その式は次のとおりです。
![]()
したがって、円の中心の座標は次のようになります。
![]()
![]()
その半径は次のとおりです。
![]()
![]()
円周B)
![]()
この円周は一般方程式の形式で表現されるため、その中心の座標を計算するには、次の式を使用する必要があります。
![]()
![]()
![]()
![]()
一方、円の半径を求める公式は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0cdc38937e6c36bb9e6d2ca0814a650_l3.png)
円周C)
![]()
円周は常方程式の形式で表され、その式は次のとおりです。
![]()
したがって、円の中心の座標は次のようになります。
![]()
この場合、方程式には項がありません。
![]()
どちらでもない
![]()
したがって、座標の原点を中心に配置されます。
![]()
その半径は次のとおりです。
![]()
![]()
演習 3
円の方程式は次のうちどれですか?
![]()
![]()
![]()
![]()
式が円の方程式になるには、次の条件が真である必要があります。
1.の係数
![]()
そしての
![]()
それらは 1 に等しくなければなりません。
2.方程式に項を含めることはできません
![]()
3.
 したがって、各方程式について 3 つの条件が満たされていることを確認する必要があります。
したがって、各方程式について 3 つの条件が満たされていることを確認する必要があります。
式A)
![]()
の係数
![]()
そして
![]()
は 1 であり、方程式には項がありません
![]()
したがって、3 番目の条件を確認するだけで十分です。

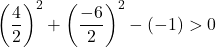
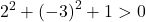
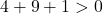
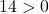 この方程式は3つの条件を満たしているので、円の方程式となります。
この方程式は3つの条件を満たしているので、円の方程式となります。
式 B)
![]()
方程式には次の項があります
![]()
この方程式は円に対応しません。
式 C)
![]()
の係数
![]()
そして
![]()
は 1 ではありませんが、すべての項を除算することで方程式を変形できます。
![]()
このようにして、次の係数は
![]()
そして
![]()
はい、それらは 1 であり、さらに、方程式には項がありません
![]()
したがって、確認する必要があるのは 3 番目の条件だけです。

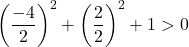
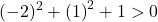
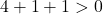
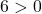 この方程式は3つの条件を満たしているので、円の方程式となります。
この方程式は3つの条件を満たしているので、円の方程式となります。
式 D)
![]()
の係数
![]()
そして
![]()
は 1 であり、方程式には項がありません
![]()
したがって、3 番目の条件を確認するだけで十分です。

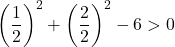
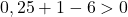
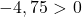 この方程式は最後の条件を満たしていないため、円の方程式ではありません。
この方程式は最後の条件を満たしていないため、円の方程式ではありません。
演習 4
次の 3 点を通る円の方程式を求めます。
![]()
任意の円の一般方程式は次のとおりです。
![]()
したがって、パラメータを見つけるには、点の座標を円方程式に代入する必要があります。
![]()
![]()
そして
![]()
の最初の点で係数を見つけます
![]()
![]()
2 番目の点で係数を求めます。
![]()
![Rendered by QuickLaTeX.com \begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-12719654d98ba81f0a7d45e587478e6d_l3.png)
そして 3 番目の点から係数を求めます。
![]()
![Rendered by QuickLaTeX.com \begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f1e69c28996a8fbfa14189c48a295095_l3.png)
結論として、円周の一般式は次のようになります。
![]()
演習 5
円の両端が次の 2 点である場合:
![]()
円の常方程式とは何ですか?
2 つの点が円の両端である場合、その中心はこれら 2 点の中点になります。
![]()
![]()
![]()
一方、円の直径は 2 点間の距離となり、2 点が形成するベクトルの大きさを使用して計算できます。
![]()
![]()
そして、円の半径は直径の半分です。
![]()
したがって、円の常方程式は次のようになります。
![]()
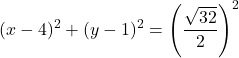
![]()
最後に、この記事が役に立ったなら、きっと双曲線 (数学)と放物線 (数学)のページにも興味を持っていただけるでしょう。双曲線と放物線とは何か、方程式、その特徴、例、演習問題などについて詳しく説明します。