▷ ニュートンの二項定理 (または二項定理)

このページでは、ニュートンの二項（または二項定理）とは何か、その公式は何なのかについて説明します。タルターリア (またはパスカル) 三角形を使用してこれを簡略化する方法もわかります。さらに、ニュートンの二項式とそのすべての特性を段階的に解く演習も用意されています。最後に、この非常に特殊な定理の起源の背後にある興味深い点について説明します。

ニュートンの二項式とは何ですか?

数学では、二項定理としても知られるニュートンの二項は、二項の累乗を簡単に計算できる公式です。言い換えれば、ニュートンの二項式は、(a+b) の形式の代数式^を解くことができる公式で構成されています。

明らかに、この定理は物理学者、数学者、哲学者であるアイザックニュートン卿にちなんで命名されました。ただし、この定理がすでに使用されていた中東の文書が発見されているため、この点に関してはいくつかの議論があります。以下では、この数式の起源について詳しく説明します。

ニュートンの二項公式

ニュートンの二項式の定義で見たように、この定理は二項式の累乗を解くために使用されます。しかし…ニュートンの二項式はどのように適用されるのでしょうか?言い換えれば、ニュートンの二項公式とは何ですか?

ニュートンの二項式の数学式は次のとおりです。

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}a^{n-k}b^k$

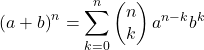
または同等のもの:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

この公式はニュートンの二項式の概念を理解するには少し複雑なので、よりよく理解できるように、以下に最低次数の二項式の累乗を示します。

ご覧のとおり、二項式を展開すると、組み合わせ数の下位要素が増加するのと同じように、第 1 項 (a) の指数が減少し、第 2 項 (b) の指数が増加します。

したがって、二項定理を使用するには、組み合わせ数、つまり次の型の代数式を解く方法を知る必要があります。

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$

。したがって、ニュートン二項式の計算方法の例を確認する前に、組み合わせ数を簡単に確認してみましょう。

組み合わせ数

組み合わせ数(または二項係数) を決定するには、次の式を適用する必要があります。

$\begin{pmatrix}n \\ k \end{pmatrix} = \cfrac{n!}{k!(n-k)!}$

金

$n!$

そして

$k!$

これらは階乗数です。階乗数は、1 からなるすべての正の整数に上記の数を乗算することによって計算されることも覚えておいてください。

$n! = 1 \cdot 2 \cdot 3 \cdots (n-1) \cdot n$

例として、組み合わせ番号を見つけて、それがどのように行われるかを確認します。

$\begin{pmatrix} 4\\ 3 \end{pmatrix} = \cfrac{4!}{3!(4-3)!}=\cfrac{4!}{3!\cdot 1!}= \cfrac{1 \cdot 2\cdot 3 \cdot 4}{(1 \cdot 2\cdot 3) \cdot 1} = \cfrac{24}{6} = 4$

組み合わせ数値は、キーを使用して計算機を使用して決定することもできます。

$\boxed{nCr}.$

ニュートン二項式の例

二項定理とは何かを理解したところで、2 つの数値例を使用してニュートンの二項公式を適用する方法を見てみましょう。

例1

ニュートンの二項式を適用して、次の二項式の累乗を計算します。

$(x+3)^2$

もちろん、この二項式は 2 乗なので、顕著な恒等式の公式 ( 顕著な恒等式の解き方) を使って解くこともできますが、例として二項定理を使用して計算します。

まず第一に、ニュートンの二項公式を適用する必要があります。

この場合、n=2 となるため、次のようになります。

$\left( x+3\right)^2 =\begin{pmatrix} 2 \\ 0 \end{pmatrix} \right)x^2 \cdot 3^0 + \begin{pmatrix} 2 \\ 1 \end{pmatrix} x^1\cdot3^1 + \begin{pmatrix} 2 \\ 2 \end{pmatrix} x^{0}\cdot3^{2}$

よく見てください。最初に、最初の項 (x) を可能な限り最大値 (この場合は 2) に引き上げます。一方、第 2 項 (3) を可能な限り最小値 (常に 0) に引き上げます。右に向かうにつれて、第 1 項を以前よりも低い数値に引き上げ、第 2 項を以前よりも高い数値に引き上げる必要があります。

次に、組み合わせ数値を計算してみましょう。

$\left( x+3\right)^2 =1\cdot x^2\cdot 3^0 + 2\cdot x^1\cdot 3^1 + 1\cdot x^{0}\cdot 3^{2}$

力を求めて解きます。

$\left( x+3\right)^2 =1\cdot x^2\cdot 1 + 2\cdot x\cdot 3 + 1\cdot 1\cdot 9$

そして最後に、乗算を計算します。

$\left( x+3\right)^2 =x^2 + 6x + 9$

例 2

ここで、もう少し難しい問題を解いてみます。

ニュートンの二項公式を適用して、次の二項の累乗を求めます。

$(2x+1)^3$

二項定理の公式は次のとおりです。

この場合、n=3 となるため、次のようになります。

$\left( 2x+1\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)(2x)^3 \cdot 1^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^{2}\cdot 1^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^{1}\cdot 1^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^{0}\cdot 1^{3}$

組み合わせ数を計算します。

$\left( 2x+1\right)^3 =1\cdot (2x)^3 \cdot 1^0 + 3\cdot (2x)^{2}\cdot 1^1 + 3 \cdot (2x)^{1}\cdot 1^{2} + 1\cdot (2x)^{0}\cdot 1^{3}$

ここでべき乗を解きます。このためには、次の 2 つのプロパティを覚えておくことが重要です。

• 単項式を指数化すると、係数と変数も同じ指数化されます →

$(2x)^3=2^3\cdot x^3 =8\cdot x^3 =8x^3$

• 項を 0 にすると 1 になります →

$(2x)^0=1$

したがって、次の 2 つの特性を通じて力を求めます。

$\left( 2x+1\right)^3 =1\cdot 2^3x^3 \cdot 1 + 3\cdot 2^2x^{2}\cdot 1 + 3 \cdot 2^1x^{1}\cdot 1 + 1\cdot 1\cdot 1$

$\left( 2x+1\right)^3 =1\cdot 8x^3 \cdot 1 + 3\cdot 4x^{2}\cdot 1 + 3 \cdot 2x\cdot 1 + 1\cdot 1\cdot 1$

最後に、項を掛け合わせます。

$\left( 2x+1\right)^3 =8x^3 + 12x^{2}+6x + 1$

ニュートンの二項式とタルターリア (またはパスカル) の三角形

上の例で見たように、組み合わせ数値の計算は少し面倒です。パスカルの三角形としても知られるタルターリアの三角形を使用して、それらの価値を直接知ることができるため、組み合わせ数を解く必要がないようにするためのトリックを教えます。

それが何であるかわからない場合のために説明すると、タルターリアの三角形 (パスカルの三角形とも呼ばれます) は、三角形の形に配置された数値の数学的表現です。

タルターリアまたはパスカルの三角形を作成するには、三角形の頂点 (常に 1) から開始し、次に下の線の番号を決定する必要があります。次の行の各数値は、行の終端が常に 1 である場合を除き、そのすぐ上の 2 つの数値の合計に等しくなります。

したがって、タルターリアの三角形のこれらの数値はそれぞれ、組み合わせ数値の結果に対応します。次の図を見てください。

たとえば、二項係数

$\begin{pmatrix} 3 \\ 1 \end{pmatrix}$

タルターリアの三角形ではその位置に 3 があるため、は 3 に相当します。

したがって、タルターリア (またはパスカル) の三角形を使用すると、組み合わせ数の計算が不要になるため、ニュートンの二項式をより迅速に解くことができます。

たとえば、次のような二項式の増強を行いたい場合:

$(x+5)^3$

ニュートンの二項則を適用すると、次の代数式が得られます。

$\left(x+5\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)x^3 \cdot 5^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 5^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 5^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 5^{3}$

組み合わせ数を 1 つずつ計算する代わりに、各組み合わせ数を対応するタルターリア三角形の係数に置き換えるだけで済みます。この場合、二項式は 3 番目まで引き上げられるため、三角形の 3 番目のレベルに対応します。

$\left(x+5\right)^3 =\color{red} \bm{1} \color{black} \cdot x^3 \cdot 5^0 + \color{red} \bm{3} \color{black} \cdot x^{2}\cdot 5^1 + \color{red} \bm{3} \color{black} \cdot x^{1}\cdot 5^{2} +\color{red} \bm{1} \color{black} \cdot x^{0}\cdot 5^{3}$

あとは残りの操作を行うだけです。

$\left(x+5\right)^3 =1 \cdot x^3 \cdot 1 + 3\cdot x^{2}\cdot 5 + 3 \cdot x\cdot 25 +1\cdot 1\cdot 125$

$\left(x+5\right)^3 =x^3+ 15x^2 + 75x +125$

ご覧のとおり、タルターリア (またはパスカル) の三角形は、これまでに示したように、より簡単かつ高速な方法でニュートンの二項式を計算するために使用されます。このため、これを使用することをお勧めします。

これまでに見てきたことを要約するために、タルターリア (またはパスカル) 三角形の数を使用したニュートンの二項式の式がどのようなものかを示す画像を示します。

負のニュートン二項式: 減算の累乗

これまでのところ、私たちが解いたニュートンの二項式の例はすべて加算でした。一方、二項式の 2 つの項のうちの 1 つが負の符号を持つ場合、手順は同様ですが、少し異なります。

二項式の項の 1 つが負である場合、つまり (ab) ⁿ型の減算である場合、ニュートン二項式の展開の符号は + – + – + – + – … の形式で交互に代わる必要があります。

以下では、二項定理とすでに設定されているタルターリア三角形の係数を使用して、最初の 5 次の負の二項の累乗を展開しています。これにより、必要な二項式を直接見つけることができます。

ニュートン二項式の性質

ニュートンの二項式には次の特徴があります。

ニュートンの二項式を分解すると、常に二項式の次数よりも 1 つの項が多くなります。言い換えれば、ペアにとって
$(a+b)^n$

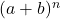
彼らは影響を受けています

$n+1$

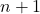
条項。
エレメントの力
$a$

皮切りに

$n$

そして最後の四半期で 0 になるまで減少します。
エレメントの力
$b$

それらは反対方向に進みます。0 から始まり、0 に達するまで増加します。

$n$

最後の学期に。
ニュートンの二項式の各要素について、次の指数の合計
$a$

そして

$b$

に等しい

$n.$
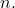
ニュートンの二項式の最初の項の係数は常に 1 (正) で、2 番目の係数は二項式の指数 (正または負) に相当します。

ニュートン二項式の k 番目の項を計算します

これは珍しいことですが、ニュートンの二項展開を行う代わりに、ニュートンの二項式の k 番目の項、つまり k の位置を占める項を決定する必要があるという問題に遭遇することがあります。

したがって、ニュートンの二項式の k の位置を占める項を計算するには、二項式が加算であるか減算であるかに応じて次の式を使用する必要があります。

ニュートンの二項式が正の場合、k 番目の項の値は次の式で計算されます。

$(a+b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}$

ニュートンの二項式が負の場合、k 番目の項の値は次の式で決定されます。

$(a-b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}$

例として、次の 5 次の二項式の第 4 項を見つけます。

$(x+3)^5$

これは合計で構成される二項なので、最初の式を適用します。

$T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}$

式内の変数を対応する値に置き換えます。

$T_4 = \begin{pmatrix} 5 \\ 4-1 \end{pmatrix} x^{5-4+1}\cdot 3^{4-1}$

そして、次の操作を実行します。

$T_4 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} x^{2}\cdot 3^{3}$

$T_4 = 10 \cdot x^{2}\cdot 27$

$T_4 = 270 x^{2}$

このようにして、他のすべての項を計算する必要なく、ニュートンの二項展開の第 4 項を計算しました。

ニュートンの二項式の演習問題を解決しました

二項定理とは何かを説明したところで、ニュートンの二項定理に関する段階的な演習をいくつか用意して、練習できるようにします。また、ご質問やご提案がございましたら、コメント欄に残していただけますようお願いいたします。

演習 1

二項定理を使用して次の二項累乗を展開します。

$(x+4)^3$

解決策を見る

まずニュートンの二項公式を使用します。

$\left(x+4\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} x^3 \cdot 4^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 4^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 4^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 4^{3}$

二項式は 3 乗されるため、タルターリア三角形の 3 番目のレベルを調べて、組み合わせ数を直接見つけます。

$(x+4)^3 = 1\cdot x^3 \cdot 4^0+3 \cdot x^2 \cdot 4^1 + 3 \cdot x^1 \cdot 4^2+1 \cdot x^0 \cdot 4^3$

私たちは次の権限を実行します。

$1\cdot x^3 \cdot 1 + 3 \cdot x^2 \cdot 4+ 3 \cdot x \cdot 16 +1 \cdot 1 \cdot 64$

そして最後に次のように乗算します。

$x^3 + 3x^2 \cdot 4 + 3 x \cdot 16 + 64$

$\bm{x^3 + 12x^2 + 48 x + 64}$

演習 2

ニュートンの二項公式を使用して次のべき乗を計算します。

$(3x+2)^3$

解決策を見る

まず、ニュートンの二項公式を適用します。

$\displaystyle \left(3x+2\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} (3x)^3 \cdot 2^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (3x)^{2}\cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (3x)^{1}\cdot 2^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (3x)^{0}\cdot 2^{3}$

二項式は 3 乗なので、組み合わせ数の値を直接知るためにパスカルの三角形の 3 番目のレベルを調べます。

$\left(3x+2\right)^3 = 1\cdot (3x)^3 \cdot 2^0+3 \cdot (3x)^2 \cdot 2^1+ 3 \cdot (3x)^1 \cdot 2^2+1 \cdot (3x)^0 \cdot 2^3$

単項式の累乗を計算します。

$1\cdot 27x^3 \cdot 1+ 3 \cdot 9x^2 \cdot 2+3 \cdot 3x \cdot 4 + 1 \cdot 1 \cdot 8$

そして最後に、乗算を実行します。

$27x^3 + 27x^2 \cdot 2 +9x \cdot 4+8$

$\bm{27x^3 + 54x^2 +36x+8}$

演習 3

ニュートンの二項公式を使用して次の多項式を展開します。

$(2x-2)^3$

解決策を見る

まず、ニュートンの二項公式を使用します。ただし、括弧内に減算があるため、各項の係数の符号を交互に切り替える必要があります。

$(2x-2)^3=\begin{pmatrix} 3 \\ 0 \end{pmatrix} (2x)^3 \cdot 2^0-\begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^2 \cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^1 \cdot 2^2-\begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^0 \cdot 2^3$

二項式は 3 乗されるため、タルターリア三角形の 3 番目のレベルを調べて、組み合わせ数を直接計算します。

$(2x-2)^3=1\cdot (2x)^3 \cdot 2^0-3 \cdot (2x)^2 \cdot 2^1 + 3 \cdot (2x)^1 \cdot 2^2-1 \cdot (2x)^0 \cdot 2^3$

私たちは次の権限を実行します。

$1\cdot 8x^3 \cdot 1- 3 \cdot 4 x^2 \cdot 2+ 3 \cdot 2x \cdot 4-1 \cdot 1 \cdot 8$

そして乗算を解きます。

$8x^3 - 12 x^2 \cdot 2 +6x \cdot 4 -8$

$\bm{8x^3 -24 x^2 +24x -8}$

演習 4

次の式を使用して、次のニュートン二項式の展開式を求めます。

$(4x-3y)^4$

解決策を見る

ニュートンの二項式の一般式を適用する必要がありますが、この場合は括弧内に減算があるため、各項の符号を交互に配置する必要があります。

$\begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}$

二項式が 4 番目に引き上げられるため、タルターリア三角形のレベル 4 を見て、組み合わせ数を直接見つけます。

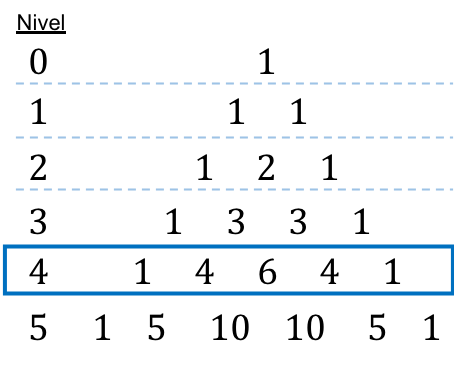
$\begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}$

私たちはすべての力を認識しています。

$1\cdot 256x^4 \cdot 1-4\cdot 64x^3 \cdot 3y+6 \cdot 16x^2 \cdot 9y^2 - 4 \cdot 4x \cdot 27y^3+1 \cdot 1 \cdot 81y^4$

そして最後に、乗算を解きます。

$256x^4-256x^3 \cdot 3y+96x^2 \cdot 9y^2 - 16x \cdot 27y^3+81y^4$

$\bm{256x^4-768x^3y+864x^2y^2-432xy^3+81y^4}$

演習 5

次の二項式の展開の 7 番目の項を決定します。

$(2x-5y)^{10}$

解決策を見る

これは負の二項なので、次の式を使用する必要があります。

$T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}$

項 7 を決定したいのですが、二項式は 10 乗されるため、式に値を代入すると次のようになります。

$T_7= (-1)^{7-1} \begin{pmatrix} 10 \\ 7-1 \end{pmatrix} (2x)^{10-7+1} \cdot (5y)^{7-1}$

したがって、次の用語を理解するには操作を行うだけで十分です。

$\begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}$

ニュートンの二項式の歴史

二項定理の起源は有名なイギリスの科学者アイザックニュートン (1642-1727) によるものとされていますが、実際には、この定理の最初の定式化は 1000 年頃にペルシャの技術者アルカリジーによって初めて発見されました。 13 世紀には、中国の数学者楊輝と朱世傑はすでに小さな次数の二項展開を知っていました。

その後 17 世紀に、ニュートンは以前の数学者が築いた基礎を基礎にして二項定理を拡張しました。数学者ジョンウォールズの内挿と外挿の方法、および一般化指数の概念を使用して、彼は多項式を無限級数に変換することができました。

1665 年頃、ニュートンは、二項定理の指数 n が有理指数になり得ること、つまり、指数が分数の場合にも二項累乗を解くことができることを証明することに成功しました。一方、負の指数の場合でも証明されました。そして驚くべきことに、彼は 2 つの式の展開が項の無限級数であることを発見しました。

この発見をきっかけに、ニュートンは無限級数と有限多項式の関係に疑問を持ち始め、無限級数でも有限多項式と同じように数学的な演算が実行できると推測しました。ニュートンはこの定理を発表しませんでしたが、ジョンウォールズは最終的に 1685 年に発表し、この発見はニュートンの功績であると認めました。

ニュートンの二項 (二項定理)

ニュートンの二項式とは何ですか?

ニュートンの二項公式

組み合わせ数

ニュートン二項式の例

例1

例 2

ニュートンの二項式とタルターリア (またはパスカル) の三角形

負のニュートン二項式: 減算の累乗

ニュートン二項式の性質

ニュートン二項式の k 番目の項を計算します

ニュートンの二項式の演習問題を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

ニュートンの二項式の歴史

コメントする返信をキャンセル

ニュートンの二項式とは何ですか?

ニュートンの二項公式

組み合わせ数

ニュートン二項式の例

例1

例 2

ニュートンの二項式とタルターリア (またはパスカル) の三角形

負のニュートン二項式: 減算の累乗

ニュートン二項式の性質

ニュートン二項式の k 番目の項を計算します

ニュートンの二項式の演習問題を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

ニュートンの二項式の歴史

コメントする 返信をキャンセル

コメントする返信をキャンセル