この記事では、不確定性とは何かについて説明します。あらゆる種類の不確実性とは何か、そしてそれらを解決する方法を発見します。さらに、すべての不確定性の関数極限について段階的に解かれた演習を見ることができます。
不確定性とは何ですか?
不定形式とも呼ばれる不定は、結果が定義されていない関数の極限の計算に現れる数式です。したがって、制限の不確定性を解決するには、関数の種類に応じた事前手順を適用する必要があります。
つまり、不確定性が生じた場合、それは極限が存在しない、または解くことができないということを意味するのではなく、むしろ、極限の解を見つけるために関数を変更する必要があることを意味します。
不確定の種類
不確定または不確定形式は、次のタイプに分類されます。
- 不確定性無限大マイナス無限大(∞-∞)
- ゼロ間の不確定性の数(k/∞)
- ゼロ間のゼロ不確定性(0/0)
- 無限間の無限不確定性(∞/∞)
- 不確定性 1 を無限大まで引き上げた(1 ∞ )
- ゼロの不確定性をゼロに引き上げます(0 0 )
- 無限大に対するゼロ不確定性(0・∞)
- ゼロの不確定性を無限大 (0 ∞ )に引き上げたもの
- 無限の不確定性をゼロ(∞ 0 )
次に、あらゆる種類の不確定事項を解決する方法を見ていきます。
無限マイナス無限不確定性
不定形式の無限大マイナス無限大は、2 つの非常に大きな数を引き算しますが、どちらが大きいかわからないため、ゼロに等しくなりません。したがって、無限大の差の結果は、各無限大の次数に依存します。
![]()
関数のタイプに応じて、何らかの手順を適用する必要があるため、このタイプの不確定性を解決するのは簡単ではありません。したがって、次のリンクで完全な説明を参照することをお勧めします。
ゼロ間の不確定性の数
定数をゼロで割った不定性は、有理関数の分母をキャンセルすると得られます。
![]()
このタイプの不定形式の結果は常に無限大になるか、無限大にならないか、関数の極限が存在しません。例として極限を解くことで、この不確定性がどのように計算されるかを見てみましょう。
![]()
ゼロで割った数値の不確定性が得られたので、関数の横方向の極限を計算する必要があります。
![]()
![]()
➤参照:横方向の制限とは何ですか?
関数の 2 つの横方向の限界は同じ結果を与えるため、定義により、x が 0 に近づく傾向があるときの関数の限界はマイナス無限大を与えます。
![]()
横方向の限界が異なる値を指定していた場合、この時点での関数の限界は存在しないことに注意してください。
ゼロ間の不確定性
不定極限のゼロをゼロで割ったものは非常に一般的で、分子と分母が相殺される分数をもつ関数で得られます。
![]()
このタイプの不定制限は、関数に応じて異なる方法で解決されます。たとえば、関数にルートがある場合は、別の手順を実行する必要があります。次のリンクで、このタイプの不確定性のさまざまな解決策を確認できます。
➤参照: ゼロ間のゼロ不確定性を解決する方法
無限の間の無限の不確定性
無限間の無限不確定は、通常、分数を含む関数の無限極限で発生します。不確定性は 2 つの無限大の商ですが、結果は必ずしも無限大である必要はありません。
![]()
このタイプの不定形は比較によって解決されます。つまり、分子の次数と分母の次数が観察され、どちらが大きいかによって、極限結果はどちらかになります。次のリンクですべてのケースを確認できます。
➤参照:無限間の無限限界に関する演習を解いた
不確定性 1 を無限大まで引き上げる
数学的には、 1 の累乗は1 に等しいため、1 から無限大までは 1 になると考えるかもしれません。しかし、この項は不確定性であるため、その結果をそれほど簡単に推測することはできません。
![]()
このタイプの不確定性は、次の式を適用して計算されます。
![]()
たとえば、次の制限は無限の力を与えるため不定です。
![]()
したがって、このタイプの不確定には次の公式を使用する必要があります。
![]()
したがって、無限に引き上げられた不定の制限はすでに解決されています。
ゼロの不確定性をゼロに
ゼロ乗の不確定性は、複雑な関数の範囲内で現れます。
![]()
このタイプの不確定な制限を解決するには、次の制限プロパティを使用する必要があります。
![]()
たとえば、次の制限は、不定形式の 0 の 0 乗を与えます。
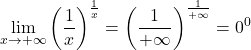
しかし、制限に対数を適用すると、その値を見つけることができます。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln\left(\frac{1}{x}\right)}}=\\[5ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln\left(\frac{1}{x}\right)}{x}}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln1-\ln x}{x}}}=\\[5ex]=\displaystyle e^{^{\displaystyle\lim_{x\to +\infty}\frac{-\ln x}{x}}}=e^{^{\displaystyle\frac{-\infty}{+\infty}}}=e^0=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04165b15f4b40bbe84ae5a4b214d4846_l3.png)
無限に対するゼロの不確定性
ゼロと無限大の積の不確定性に遭遇するのは困難ですが、それを決定するのが簡単であるという意味ではありません。
![]()
このタイプの不確定性を解決する唯一の方法はありませんが、関数のタイプによって異なります。この場合、関数を無限不確定性を無限で割ったもの、またはゼロの不確定性をゼロで割ったものに変換し、そこから各不確定性に対して上で見た解法を適用する必要があります。
したがって、1 つの関数の限界が 0 で、もう 1 つの関数の限界が ∞ の場合、次のようになります。
![]()
次の変更を加えることで、この型を無期限に変換できます。
![Rendered by QuickLaTeX.com \displaystyle\lim_{x\to a}f(x)\cdot g(x)\begin{cases}\displaystyle\lim_{x\to a}\frac{f(x)}{\displaystyle\frac{1}{g(x)}}=\frac{0}{0}\\[10ex]\displaystyle\lim_{x\to a}\frac{g(x)}{\displaystyle\frac{1}{f(x)}}=\frac{\infty}{\infty}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-df402461269ae26c30768fc0bf83f2ea_l3.png)
例として不定の制限を解決することでこれを行う方法を見てみましょう。
![]()
関数を操作して無限大にわたる無限不確定性を取得し、極限を見つけます。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=\lim_{x\to +\infty}\frac{x}{\displaystyle\frac{1}{e^{-x}}}=\\[6ex]=\displaystyle \lim_{x\to +\infty}\frac{x}{e^x}=\frac{+\infty}{e^{+\infty}}=\frac{+\infty}{+\infty}=0\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c29bbb439514449cd12fd8d66e327af_l3.png)
ゼロの不確定性を無限大まで拡張
非常に小さな数を非常に大きな数に累乗するので、不定性ゼロを無限に累乗することは少し理解しにくいです。
![]()
これらの不定形が得られる場合は、次の式を使用する必要があります。
![]()
このタイプの不確定性を計算する方法をよりよく理解するために、例を解いてみましょう。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0^+}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to 0^+}\frac{1}{x}\cdot \ln(x)}}=\\[3.5ex]\displaystyle =e^{^{\displaystyle\frac{1}{0^+}\cdot \ln(0^+)}}=e^{+\infty\cdot (-\infty)}\\[3ex]\displaystyle =e^{-\infty}=\frac{1}{e^{+\infty}}=0\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ca354428ea8889a956a9b77b04a088f_l3.png)
無限の不確定性をゼロに
通常、ゼロに累乗すると 1 になりますが、ゼロに累乗した無限大の不確定性は必ずしもこのようにする必要はありません。
![]()
ゼロをゼロに累乗したり、ゼロを無限に累乗したりする不定の場合と同様、このタイプの不定限界を解決するには、対数を適用する必要があります。
![]()
例を段階的に計算することで、このタイプの不確定な制限がどのように解決されるかを見てみましょう。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to +\infty}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln(x)}}=\\[3ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln(x)}{x}}}=e^{^{\displaystyle\frac{\ln(+\infty)}{+\infty}}}=\\[3ex]\displaystyle =e^{^{\displaystyle\frac{+\infty}{+\infty}}}=e^0=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a45090015a206189aca3884f8b2cab30_l3.png)