3 の法則により、特定の値の間に存在する比例関係を知ることができます。このおかげで、私たちは日常生活のあらゆる分野でほぼ毎日それを適用しています。例を挙げると、 パーセンテージを計算し、単位 (質量、体積、時間など) 間の変換を行い、一般に等価性に基づいて計算を行います。この最後のアプリケーションは、この数学的リソースをほぼすべての主題で使用できるようにするものです。
したがって、 3 つのルールを解決する方法を学びたい場合は、記事の最後まで読むことをお勧めします。解決方法、種類、応用例を解説し、解決例も紹介します。つまり、この記事を読み終える頃には、この数学的概念について知っておくべきことはすべてわかるでしょう。
三則計算機
3 つの計算機のこれらのルール(1 つ目は直接比例、2 つ目は間接比例) を使用すると、すべての演習をチェックして修正することができます。操作は非常に簡単で、4 つのボックスのうち 3 つに既知のデータを入力するだけで、計算ボタンをクリックすると x の値が表示されます。ただし、このタイプの計算の構成方法がまだ分からなくても、次のセクションで詳しく説明するので心配しないでください。
直接三法計算機
逆三則計算機
3つのルールをどうやって作るか?
3 の法則を解くには、まず、直接 3 の法則と間接 3 の法則のどちらを使用するかを特定する必要があります。また、単純な 3 つの規則と複合的な 3 つの規則のどちらのタイプの比例関係を使用するかを区別する必要があります。誰もがこれらのオプションのいずれかを持っているため、データを整理する方法や式も異なります。したがって、各タイプをいつ選択するかを知るには、3 の法則を解く方法に関する次の説明を読むことをお勧めします。
1. さまざまな変数間の関係を特定する
3 の法則を解くための最初のステップは、変数間の何らかの図または関係を作成することです。一般に、これは通常、以下の画像に見られる典型的な図を使用して行われます。このおかげで、計算の構造がより明確になり、後で計算を実行できるようになります。文字 A、B、C を対応する値に置き換えるだけです。左の列には全体としてわかっている大きさの数値 (両方の値) が入り、右の列には値が入ります。未知なる大きさ。また、線を尊重する必要があるため、A は変数 B に関連する左側の大きさの値でなければなりません。
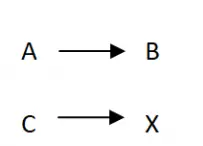
2. 3 の法則の比例関係を確立する
次のステップは、変数間の比例関係を特定することです。これは、各大きさの変数間の数値の変化を分析することによって行います。最終的に 3 の直線ルールに落ち着いた場合、一方の量が増加すると、もう一方の量も増加します。しかし、最終的に 3 の逆の法則に行き着くと、一方の量が増加すると、もう一方の量が減少します。計算式はケースごとに異なるため、これを念頭に置くことが重要です。
3. 簡単なルールまたは 3 つのルールで構成される
最後に、比例関係を使用して関連付ける変数の数に応じて、3 つのルールを 2 つのタイプに区別します。単純な 3 の法則の場合、別の量の比例関係から変数 X の値を取得します。 3 つで構成されるルールにより、2 つ以上の量の比例性に基づいて変数 X を計算できます。次に、これら 2 つの概念の公式とグラフ表現を示します。そうすれば、間違いなく理解できます。

3 つの簡単なルールの例
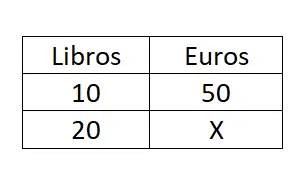
10 冊の本が 50 ユーロの場合、20 冊購入すると、いくらかかりますか?
結果を得るには、シンプルで単純な 3 つのルールを解く必要があります。したがって、式 X = (B · C) / A を使用します。
3 つのルールからなるルールの例
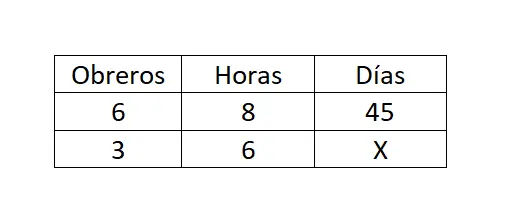
1 日 8 時間働く 6 人の労働者が 45 日で家を建てる場合、1 日 6 時間働く 3 人の労働者が同じ建設を完了するのに何日かかりますか?
この場合、3 つの複合間接ルールがあります。したがって、式 X = (A 1 · B 1 · C 1 ) / (A 2 · B 2 ) を使用します。
3 の法則の応用
冒頭でコメントしたように、3 の法則を使用すると多くのことを計算できるため、日常生活のあらゆる分野に適用できます。このタイプのアプリケーションには共通の特徴がありますが、比率を使用して計算されることです。いくつかの例を挙げると、次のようになります。
- パーセンテージの計算
- 単位間の変換
- 薬の投与量を計算する
- 手数料の計算
- 成績を計算する
実際、等価性などを必要とするほとんどすべての操作。
関数電卓の 3 つのルール
最も一般的な関数電卓には、通常、3 の法則を解くための関数やキーはありません。したがって、カスタマイズされた機能を追加できる高度な計算機がない場合、3 のルールを解くことはほとんどできません。したがって、このプロセスを個別に (紙の上または頭の中で) 実行する必要があります。次に、電卓で計算部分を実行します。最初は少し遅く感じるかもしれませんが、練習して頭の中に描いた3つのルールをイメージできるようになると、すぐに解けるようになります。
最後に、3 つの演習のルールをさらに確認したい場合は、練習用の演習へのリンクを残しておきます。とはいえ、この記事とオンラインの Rule of 3 計算ツールが、この数学的概念をより深く理解するのに役立つことを願っています。