このページでは、ヤコビアン行列とは何か、および例を使用してそれを計算する方法を説明します。さらに、練習できるように、ヤコビアン行列に関するいくつかの演習問題が解決されています。ヤコビアン行列の行列式であるヤコビアンがなぜ非常に重要なのかもわかります。最後に、このマトリックスが他の演算と維持する関係や、このマトリックスが持つアプリケーションについて説明します。
ヤコビアン行列とは何ですか?
ヤコビ行列の定義は次のとおりです。
ヤコビアン行列は、関数の一次偏導関数によって形成される行列です。
したがって、ヤコビ行列の式は次のようになります。

したがって、ヤコビアン行列には常にスカラー関数と同じ数の行が含まれます。
![]()
関数があり、列の数は変数の数に対応します
![]()
一方、この行列はヤコビアン微分マップまたはヤコビアン線形マップとも呼ばれます。実際、J の代わりに D で書かれることもあります。
![]()
興味深いことに、ヤコビ行列は、19 世紀の重要な数学者であり教授であり、数学の世界、特に線形代数の分野に重要な貢献をしたカール グスタフ ヤコビにちなんで名付けられました。
ヤコビ行列の計算例
ヤコビアン行列の概念を理解したら、例を使用してそれがどのように計算されるかを段階的に見ていきます。
- 次の関数の点 (1,2) におけるヤコビ行列を決定します。
![]()
最初に行う必要があるのは、関数のすべての 1 次偏導関数を計算することです。
![]()
![]()
![]()
![]()
次に、ヤコビアン行列の公式を適用します。この場合、関数には 2 つの変数と 2 つのスカラー関数があるため、ヤコビ行列は次元 2×2 の正方行列になります。
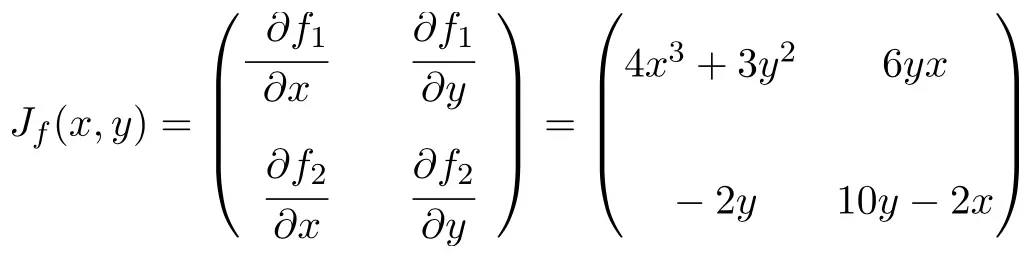
ヤコビアン行列の式を取得したら、点 (1,2) でそれを評価します。
![Rendered by QuickLaTeX.com \displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fa6ed35890b94e3abe43b9a3f9674e36_l3.png)
そして最後に、操作を実行して解決策を取得します。
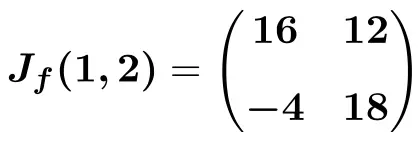
関数のヤコビアン行列を見つける方法を理解したら、練習できるように段階的に解決されるいくつかの演習を用意します。
ヤコビアン行列の問題を解決しました
演習 1
2 つの変数における次のベクトル関数の点 (0,-2) におけるヤコビ行列を求めます。
![]()
この関数には 2 つの変数と 2 つのスカラー関数があるため、ヤコビ行列はサイズ 2×2 の正方行列になります。
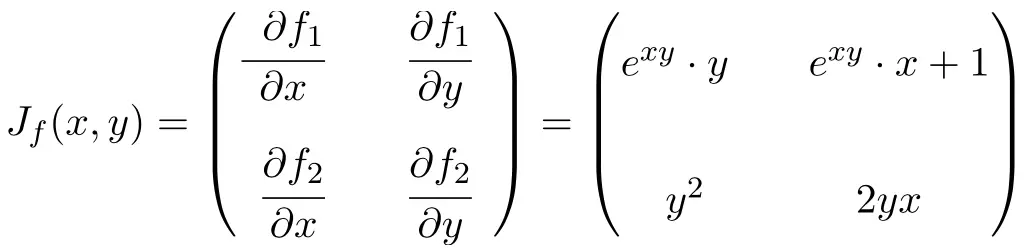
ヤコビ行列の式を計算したら、それを点 (0,-2) で評価します。
^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4f6008d8799a0a1c3a667e958d6c8818_l3.png)
そして最後に、操作を実行して結果を取得します。
![Rendered by QuickLaTeX.com \displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5eb37dc494497a424b489235b1a55a5f_l3.png)
演習 2
2 つの変数を使用して、次の関数の点 (2,-1) でのヤコビ行列を計算します。
![]()
この場合、関数には 2 つの変数と 2 つのスカラー関数があるため、ヤコビ行列は次数 2 の正方行列になります。
![Rendered by QuickLaTeX.com \displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-48baf447fc5a448f30f13295f96cb874_l3.png)
ヤコビアン行列の式が見つかったら、それを点 (2,-1) で評価します。
![Rendered by QuickLaTeX.com \displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4f2ee2de8e72eed6956f784628353547_l3.png)
そして最後に、操作を実行して結果を取得します。
![Rendered by QuickLaTeX.com \displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7935318698eadf3d3af4f87e6e8f2629_l3.png)
演習 3
3 つの変数を使用して、次の関数の点 (2,-2,2) におけるヤコビ行列を決定します。
![]()
この場合、関数には 3 つの変数と 2 つのスカラー関数があるため、ヤコビ行列は次元 2×3 の長方形行列になります。
![Rendered by QuickLaTeX.com \displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5b327537a2e4c80c7eb38d56d94bb141_l3.png)
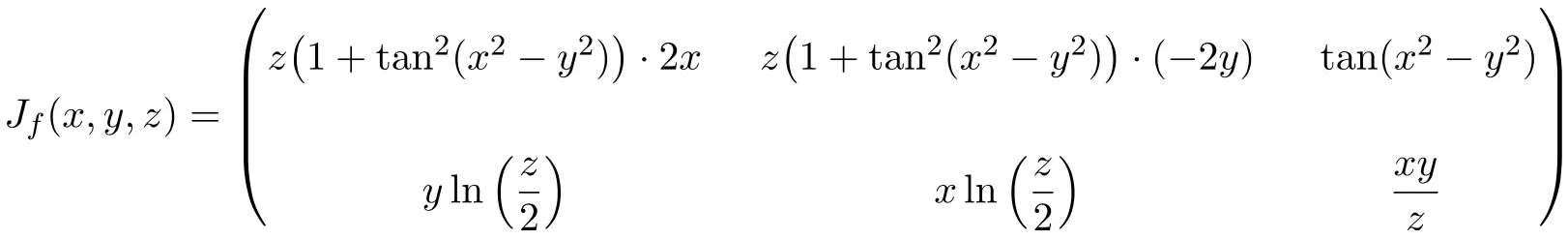
ヤコビアン行列の式を取得したら、それを点 (2,-2,2) で評価します。
![Rendered by QuickLaTeX.com \displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a62dd1b4655e9d089404028ec48fbe11_l3.png)
計算を実行します。
![Rendered by QuickLaTeX.com \displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-05c8aaa8cca0f4cb652c95b11d2e9db1_l3.png)
そして、単純化できなくなるまで操作を続けます。
![Rendered by QuickLaTeX.com \displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2b4fda9837a6287456ca469d46a2382_l3.png)
演習 4
点におけるヤコビアン行列を決定します。
![]()
次の多変数関数の
![]()
この場合、関数には 2 つの変数と 3 つのスカラー関数があるため、ヤコビ行列は次元 3×2 の長方形行列になります。
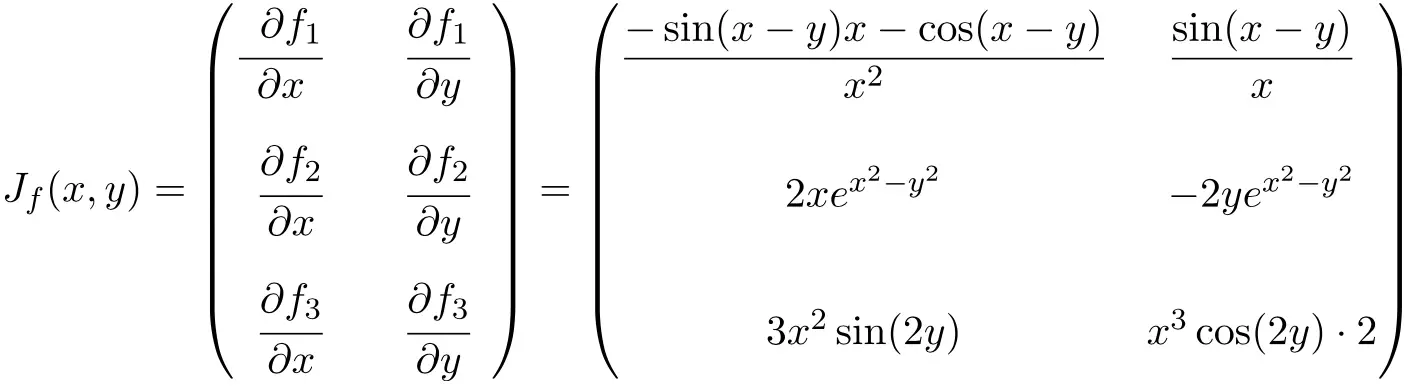
ヤコビアン行列の式を取得したら、それを次の点まで評価します。
![]()
![Rendered by QuickLaTeX.com \displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-167caa7a7d1cb34db33f7b92e21b5f78_l3.png)
私たちは次のような業務を実行します。
![Rendered by QuickLaTeX.com \displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b05c5bfee3f874f3adec324a6bc9b43e_l3.png)
したがって、考慮されている点でのベクトル関数のヤコビアン行列は次の値になります。
![Rendered by QuickLaTeX.com \displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4addee61e4664b95dbb049be217af34_l3.png)
演習 5
点でのヤコビアン行列を計算します。
![]()
3 つの変数を使用した次の関数:
![]()
この場合、関数は 3 つの変数と 3 つのスカラー関数で構成されているため、ヤコビ行列は次元 3×3 の正方行列になります。
![Rendered by QuickLaTeX.com \displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd9dcbb1d4961906d5b8581f70f5392_l3.png)
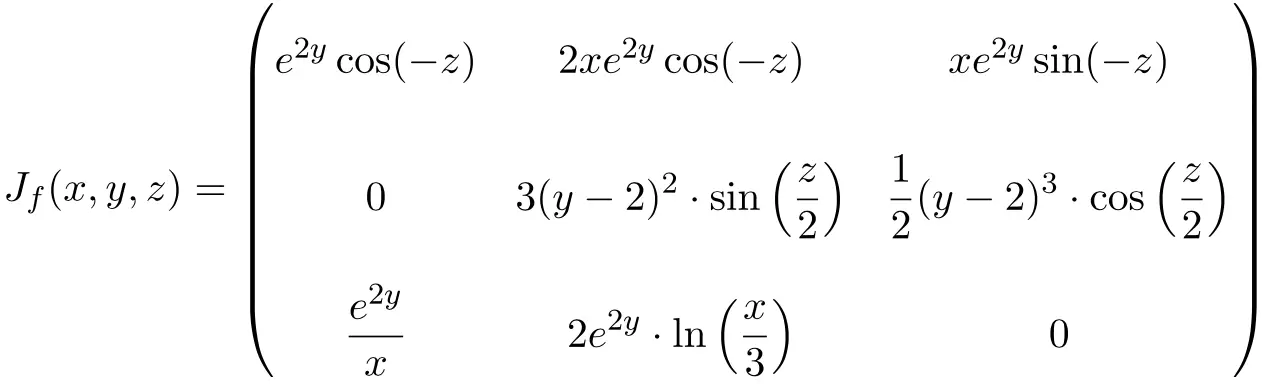
ヤコビアン行列を見つけたら、次の点で評価します。
![]()
![Rendered by QuickLaTeX.com \displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4f56df32b7632d1e74f014f0aab2b52a_l3.png)
演算を計算します。
![Rendered by QuickLaTeX.com \displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5771c5e1c54eabf6df6633abd5f3e194_l3.png)
この時点でのヤコビ行列の結果は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6dc1884b96ce985e1475c5cfcba2fff8_l3.png)
ヤコビアン行列の行列式: ヤコビアン
ヤコビアン行列の行列式はヤコビアン行列式またはヤコビアンと呼ばれます。ヤコビアン行列は、関数がスカラー関数と同じ数の変数を持つ場合にのみ計算できることを考慮する必要があります。その場合、ヤコビアン行列は行数と列数が同じになり、したがって正方形になります。マトリックス。 。
ヤコビアンの例
2 つの変数を持つ関数のヤコビアン行列式を計算する例を見てみましょう。
![]()
まず関数のヤコビアン行列を計算します。
![Rendered by QuickLaTeX.com \displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5870e75f368ea3e554b2fa32cfa554dc_l3.png)
次に、2×2 行列の行列式を解きます。
![Rendered by QuickLaTeX.com \displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d1ef9df1d4735e3cea235c653714439_l3.png)
ヤコビアンと関数の可逆性
ヤコビアンの概念を見てきたので、おそらく次のように考えたでしょう…それで、何が意味があるのでしょうか?
ヤコビアンの主な用途は、関数を逆にできるかどうかを判断することです。逆関数定理は、ヤコビアン行列 (ヤコビアン) の行列式が 0 と異なる場合、この関数は可逆であることを意味します。
![]()
この条件は必要ですが十分ではないことに注意してください。つまり、行列式が 0 以外の場合、行列は反転できると断言できますが、行列式が 0 の場合、行列式が 0 であるかどうかはわかりません。関数には逆数または No があります。
たとえば、関数のヤコビアンを見つける方法について前述した例では、行列式は次のようになります。
![]()
。この場合、関数は点 (0,0) を除いて常に反転できると断言できます。これは、この点がヤコビアン行列式が 0 に等しい唯一の点であるため、逆関数かどうかはわかりません。この点に存在します。
ヤコビアン行列と他の演算との関係
ヤコビアン行列は、関数の勾配とヘッセ行列に関連します。
スロープ
関数がスカラー関数の場合、ヤコビ行列はgradientと等価な行行列になります。
![]()
![]()
ヘシアン行列
関数の勾配のヤコビアン行列はヘッセ行列と等しくなります。
![]()
ヘッセ行列は、関数の 2 次導関数によって形成されるため、複数の変数を含む関数を導出する場合に非常に重要な行列です。実際、ヘッセ行列はヤコビ行列の連続性であると言えます。しかし、これは非常に重要なので、ページ全体で詳細に説明しています。したがって、このマトリックスが何であるか、そしてなぜそれがそれほど特別なのかを正確に知りたい場合は、リンクをクリックしてください。
ヤコビ行列の応用
関数が可逆かどうかを決定するヤコビアンの有用性以外にも、ヤコビアン行列には他の用途もあります。
ヤコビアン行列は、多変量関数の臨界点を計算するために使用され、ヘッセ行列を通じて最大値、最小値、または鞍点に分類されます。臨界点を見つけるには、関数のヤコビ行列を計算し、それを 0 に設定し、結果の方程式を解く必要があります。
![]()
さらに、ヤコビ行列の別の応用は、複数の変数を含む関数の積分、つまり二重積分、三重積分などに見られます。ヤコビ行列の行列式により、次の式に従って重積分の変数を変更できるため、
![]()
![]()
ここで、 T は、元の変数を新しい変数に関連付ける変数変更関数です。
最後に、ヤコビ行列は関数の線形近似を行うためにも使用されます。
![]()
点の周り
![]()
:
![]()