このページでは、ベクトルと実数 (またはスカラー) を乗算する方法を数値およびグラフィックで説明します。さらに、ベクトルとスカラーの積の例と演習問題も見つかります。最後に、ベクトルを使用したこのタイプの演算のプロパティについても説明します。
ベクトルに実数を掛けるにはどうすればよいでしょうか?
ベクトルと数値 (またはスカラー) の積を数値的に計算するには、ベクトルの各成分に数値を乗算する必要があります。
![]()
![]()
したがって、ベクトルに数値を乗算した結果、次の特性を持つ新しいベクトルが生成されます。
- ベクトルとスカラーの積の結果、元のベクトルと同じ方向の新しいベクトルが生成されます。
- さらに、数値が正の場合、新しいベクトルは同じ方向になります。
- または、数値が負の場合は逆の意味になります。
- 結果として得られるベクトルの大きさは、元のベクトルの大きさにスカラーを掛けたものと等価です。
次のグラフでは、スカラーの符号に関係なく、ベクトルの方向がどのように維持されるかがわかります。一方、ベクトルの方向は、ベクトルに乗算する数値の符号に依存します。

さらに、次のグラフでは、結果の積ベクトルの大きさが、元のベクトルにスカラーを乗算した大きさに等しいことが明確にわかります。
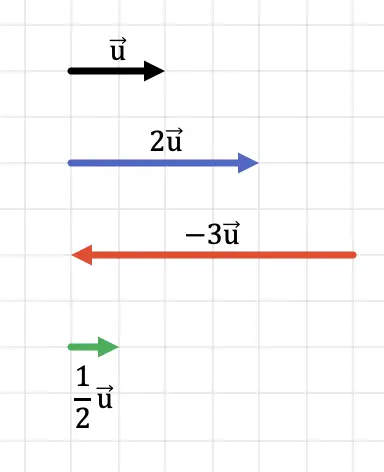
明らかに、ベクトルに 1 より大きい数値を乗算すると、結果はより長い長さの (より大きな係数の) ベクトルになります。一方、ベクトルに 1 未満の数値を乗算すると、結果は長さの短い (係数が小さい) ベクトルになります。
注:ベクトルとスカラーの積と、 ベクトルの内積を混同しないでください。名前は似ていますが、この 2 つはまったく異なる概念です。
ベクトルとスカラーの積の例
次に、ベクトルと数値の積を計算する方法の数値例を見ていきます。
- 次のベクトルを 4 倍します。
![]()
![]()
ご覧のとおり、このタイプのベクトル演算は多くの計算を行う必要がないため、それほど複雑ではありません。
ただし、ベクトル加算やベクトル減算など、より複雑なベクトル演算もあります。ベクトルとスカラーの積を計算する方法をすでに理解している場合は、次のレベルに進んで、 ベクトルの加算とベクトルの減算を解決する方法を確認することをお勧めします。これらはやや難しい演算であり、実際には次のとおりです。それらははるかに多く使用されます(より重要です)。
ベクトルと数値の乗算のプロパティ
ベクトルと数値の積には次の特性があります。
- 結合プロパティ: ベクトルに複数の数値を乗算する場合、乗算の順序は関係ありません。
![]()
- ベクトルの加算と減算に関する分配特性:
![]()
![]()
- スカラーの加算に関する分配特性:
![]()
- 中立要素: 明らかに、任意のベクトルに 1 を乗算すると、ベクトル自体が得られます。
![]()
ベクトルとスカラーの乗算の問題を解決しました
演習 1
次のベクトルと 3 の積の結果を分析的に計算します。
![]()
積を求めるには、ベクトルの各座標を 3 で乗算する必要があります。
![]()
演習 2
次のベクトルを 6 で乗算し、そのモジュールを求めます。
![]()
まずベクトルにスカラーを乗算します。
![]()
取得されたベクトルの大きさを計算する方法は 2 つあります。 1 つ目は、元のベクトルの大きさを求め、それを 6 で乗算します。
![]()
![]()
2 番目の方法は、乗算で得られたベクトルの大きさを直接計算することです。
![]()
したがって、どちらの手順でも、結果は係数の計算方法に依存しないことがわかります。
演習 3
次のベクトルから:
![]()
次の演算を代数的に計算します。
![]()
![]()
![]()
![]()
次に、結果のベクトルが元のベクトルと同じ方向と方向を持っているかどうかを判断し、最短から最長の順に並べます。
まず乗算を計算します。
![]()
![]()
![]()
![]()
したがって、正の数を掛けたベクトルは、元のベクトルと同じ方向と方向を持ちます。また、負の数を掛けたベクトルは、元のベクトルと同じ方向ですが逆の方向になります。
同じ方向と同じ方向のベクトル:
![]()
そして
![]()
同じ方向だが意味が異なるベクトル:
![]()
最後に、ベクトルをその長さ、つまりモジュールに従って順序付けする必要があります。最長の長さのベクトル (または最大のモジュール) は、(絶対値で) より大きな数を乗算したものとなり、最短の長さのベクトル (または最小のモジュール) は、より小さい数を乗算したものになります。数値 (絶対値)。したがって、長さの順序は次のようになります。
![]()
ベクトルの方向によって係数が変更されないため、長さまたは係数は乗算されるスカラーの符号に依存しないことに注意してください。
演習 4
次の 2 つのベクトルを考えてみましょう。
![]()
次の演算を計算します。
![]()
まずベクトルと数値の乗算を解きます。
![]()
![]()
![]()
そしてベクトルを減算します。
![]()
![]()
演習 5
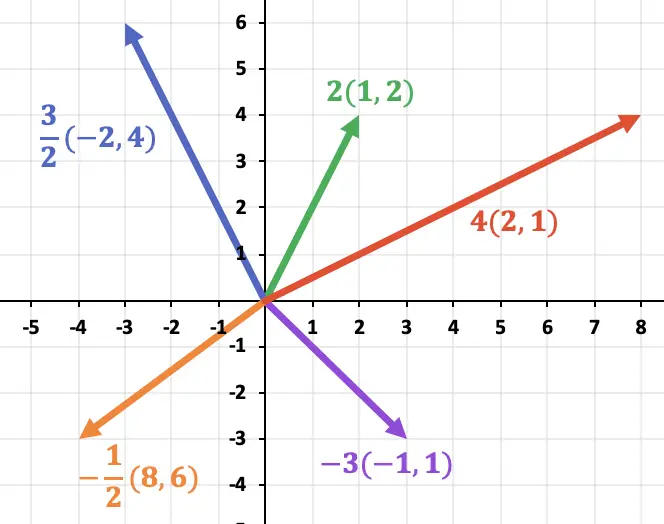
次のベクトルとスカラーの乗算を実行し、結果をグラフにします。
![]()
![]()
![]()
![]()
![]()
まずベクトルに実数スカラーを乗算します。
![]()
![]()
![]()
![]()
![]()
最後に、ベクトルを計算したら、それらをグラフに表します。