このページでは、ガウス・ジョーダン法とは何か、およびガウス法を使用して連立方程式を解く方法を学習します。さらに、ガウス法を実践して完全に理解できるように、ガウス法を使用したシステムの例と演習問題も掲載されています。
ガウス法とは何ですか?
ガウス・ジョルダン法は、 3 つの未知数を含む連立方程式を解くために使用される手順です。つまり、次のようになります。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x-4y+5z=10 \\[2ex] x+5y-2z=4 \\[2ex] -x+4y+2z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-088146ef83bbd007e82aca8189434c25_l3.png)
ガウスの方法の目的は、初期方程式系を段階的な系、つまり各方程式の未知数が前のものより 1 つ少ない系に変換することです。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{array} \right\} \ \bm{\longrightarrow} \left. \begin{array}{r} A_1x+B_1y+C_1z=D_1 \\[2ex] B_2y+C_2z=D_2 \\[2ex] C_3z=D_3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-10926b0856ae512c737ae924bd9413a1_l3.png)
ただし、これを行うには、まず連立方程式を行列形式で表現する方法と、この行列で許可される変換を知っておく必要があります。したがって、これら 2 つのことを前に説明し、その後、ガウス法の手順を使用する方法を見ていきます。
システム拡張マトリックス
この系がどのように解かれるかを確認する前に、連立方程式が行列の形式で表現できることを知っておく必要があります。
![]()
の係数が最初の列に入れられます。
![]()
2 番目の列には、
![]()
3 列目には未知数を含まない数字が 4 列目に表示されます。
例えば:
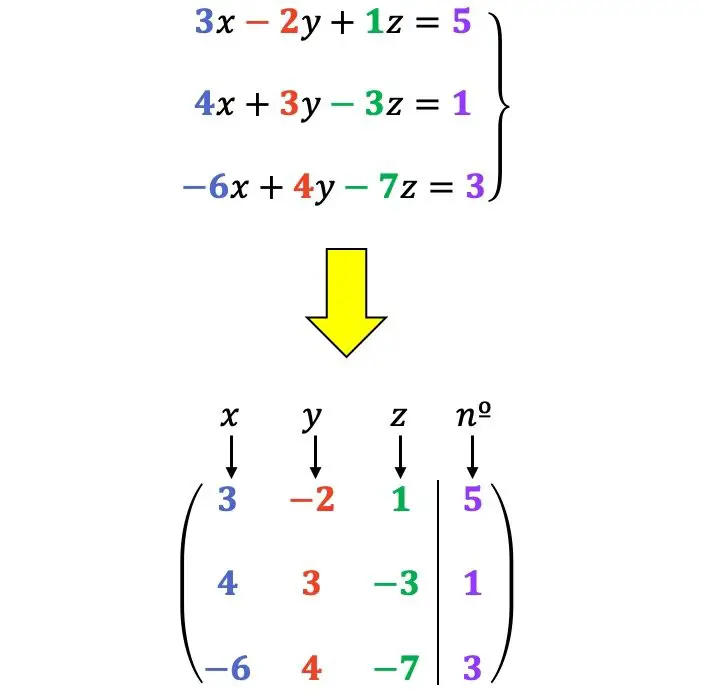
許可される行変換
方程式系をスケーリングされた系に変換するには、系に関連付けられた行列に対して次の操作のいずれかを実行できます。
- マトリックスの行の順序を変更します。
たとえば、行列の 2 行目と 3 行目の順序を変更できます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] -2 & 4 & -1 & 2 \\[2ex] 6 & 1 & -3 & 10 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] 6 & 1 & -3 & 10 \\[2ex] -2 & 4 & -1 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ee0e251559ef9dfd02c9b0105f934af8_l3.png)
- 行内のすべての項を 0 以外の数値で乗算または除算します。
たとえば、行 1 を 4 で乗算し、行 3 を 2 で割ることができます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 2 & -4 & -2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc|c} 4 & -8 & 12 & 4 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 1 & -2 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e1f081c9056075ede064b2e5c9e4193_l3.png)
- 行を、同じ行と別の行の合計に数値を乗算した値に置き換えます。
たとえば、次の行列では、行 2 を行 3 に加算し、1 を乗算します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 2 & 4 & 1 & -5 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1 \cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 3 & 2 & 4 & -6 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-04417e2094ac05c7a374334c55197f36_l3.png)
ガウス法を使用して連立方程式を解くにはどうすればよいですか?
ここでは、ガウス法を使用して連立方程式を解く手順を例を通して見ていきます。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} -x+2y+2z=-24 \\[2ex] x+y+z=48 \\[2ex] 2x-6y+4z=12 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61e6e829301e6730c9e27f9c0a30de2e_l3.png)
最初に行うことは、システムの拡張行列です。
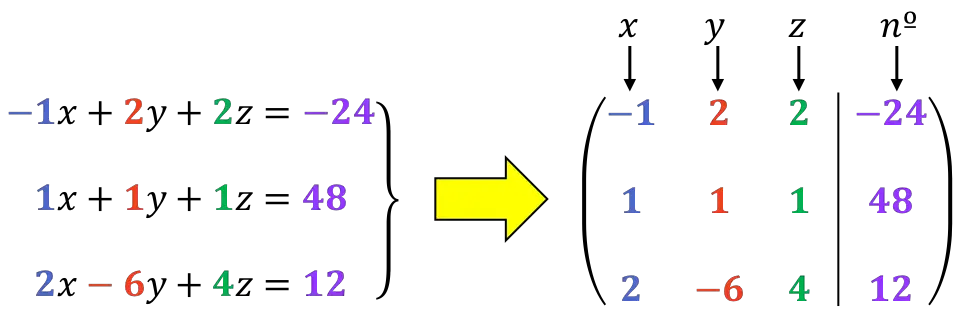
後で説明するように、最初の行の最初の桁は 1 である方がよいため、 1 行目と 2 行目の順序を変更します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} -1 & 2 & 2 &-24 \\[2ex] 1 & 1 & 1 & 48 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \xrightarrow{ f_1 \rightarrow f_2} \\[2ex] \xrightarrow{ f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} \color{blue}\boxed{\color{black}1} & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 &-24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b45e0f757ca2880442314f6a4800697b_l3.png)
ガウスの方法の目標は、主対角線の下の数値を 0 にすることです。つまり、赤い数字を 0 に変換する必要があります。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{red}\bm{-1} & 2 & 2 &-24 \\[2ex] \color{red}\bm{2} & \color{red}\bm{-6} & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-28164ac6b48d32c09b4725548c0633f6_l3.png)
これらの数値を削除するには、行の適切な変換を実行する必要があります。
たとえば、2 行目の最初の要素である -1 は、1 行目の最初の要素である 1 の負の数です。したがって、最初の行を 2 行目に追加すると、 -1 が削除されます。

したがって、この合計を実行すると、次の行列が得られます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 & -24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{blue}\boxed{\color{black}0} & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b106306b92bfc3e99d602c22d5198bd_l3.png)
このようにして、-1 を 0 に変換することができました。
ここで 2 を変換します。お気づきのとおり、3 行目の最初の要素である 2 は、1 行目の最初の要素である 1 の 2 倍です。したがって、最初の行に -2 を掛けた値を 3 番目の行に追加すると、 2 は消去されます。
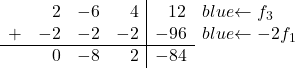
したがって、次の行列が得られます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] \color{blue}\boxed{\color{black}0} & -8 & 2 & -84 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-36b2fdf8de855cf35049ecefcf7c1da5_l3.png)
このようにして、2 を 0 に変換することができました。
ここでしなければならないのは、-8 を 0 に変換することだけです。これを行うには、 3 行目を 3 で乗算し、2 行目を 8 で乗算したものを追加します。
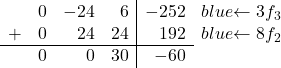
したがって、次の行列が得られます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & -8 & 2 & -84 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3f_3 + 8f_2} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & 30 & -60 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e2324629222c746a9021ce05ba7d54d_l3.png)
これらの変換により、主対角線より下のすべての数値が 0 になりました。これで、連立方程式を解くことができます。
次に、行列を未知数を含む連立方程式に変換する必要があります。これを行うには、最初の列が
![]()
の 2 列目
![]()
の 3 列目
![]()
最後の列は未知数を除いた数値です。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & 0 & 30 & -60 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x+1y+1z=48 \\[2ex] 3y+3z=24 \\[2ex] 30z=-60 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f90de9d9f5a06959a2d4aebf05f4758_l3.png)
そして最後に、システムを解くには、方程式の未知数をボトムアップで解く必要があります。最後の方程式には未知数が 1 つだけあるため、それを解いてその値を見つけることができます。
![]()
![]()
![]()
z が何であるかがわかったので、その値を 2 番目の方程式に代入すると、次の値が得られます。
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
そして、最初の方程式でも同じことを行います。他の未知数の値を代入し、消去します。
![]()
:
![]()
![]()
![]()
![]()
したがって、連立方程式の解は次のようになります。
![]()
ガウス・ジョルダン法による連立方程式の問題の解決
演習 1
ガウス法を使用して次の連立方程式を解きます。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854043b0e7e3e2166593dcf5c645bfa0_l3.png)
最初に行う必要があるのは、システムの拡張行列です。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b6369a58b91f31bf4c8bc212ccf68c6_l3.png)
次に、メイン配列の下のすべての数値を 0 にする必要があります。
したがって、行演算を実行して、最初の列の最後の 2 つの項をキャンセルします。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3-2f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cd42dcf61aebc4c67de13e09dff72f4b_l3.png)
次に、2 番目の列から最後の要素を削除します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-13945337848a6f1badf6efe249951124_l3.png)
主対角線より下のすべての数値が 0 になると、連立方程式を解くことができます。これを行うには、行列を未知数を含む連立方程式の形式で再度表現します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y-z=2 \\[2ex] -3y+4z=-2 \\[2ex] 1z=1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f068c276aae018a668cc005bcad3e641_l3.png)
そして方程式の未知数を下から上に解きます。まず最後の方程式を解きます。
![]()
![]()
次に、z の値を 2 番目の方程式に代入して、y の値を求めます。
![]()
![]()
![]()
![]()
![]()
そして、最初の方程式でも同じことを行います。他の未知数の値を代入し、x を解きます。
![]()
![]()
![]()
![]()
したがって、連立方程式の解は次のようになります。
![]()
演習 2
ガウス法を使用して、次の方程式系の解を求めます。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d0595899b8137f769c74fce1b21286b_l3.png)
最初に行う必要があるのは、システムの拡張行列です。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e2a16b6d1451520bd8898675c022dc2_l3.png)
ガウス法を適用するには、最初の行の最初の数値が 1 であれば簡単です。したがって、1 行目と 2 行目の順序を変更します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1\rightarrow f_2} \\[2ex] \xrightarrow{f_2\rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef7e2e42d0eecb0395afb7c8311b2ade_l3.png)
次に、メイン配列の下のすべての数値を 0 にする必要があります。
したがって、行操作を実行して、最初の列の最後の 2 つの要素を置き換えます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] \xrightarrow{f_3-4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-40baaee3bbde9ed1577e00bc1c3b338f_l3.png)
次に、2 番目の列の最後の要素をゼロに変換します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f328906485bfe6ee77833c04869e1240_l3.png)
主対角線より下のすべての数値が 0 になると、連立方程式を解くことができます。これを行うには、行列を未知数を含む連立方程式の形式で再度表現します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+2z=5 \\[2ex] -5y-2z=-13 \\[2ex] -5z=5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7e129715c720218a5cb25ef07442442_l3.png)
そして方程式の未知数を下から上に解きます。まず最後の方程式を解きます。
![]()
![]()
次に、z の値を 2 番目の方程式に代入して、y の値を求めます。
![]()
![]()
![]()
![]()
![]()
そして、最初の方程式でも同じことを行います。他の未知数の値を代入し、x を解きます。
![]()
![]()
![]()
![]()
したがって、連立方程式の解は次のようになります。
![]()
演習 3
ガウス法により次の連立方程式の解を計算します。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4301eae3179543fbdee7568e8f88aa4c_l3.png)
最初に行う必要があるのは、システムの拡張行列です。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c0d96160d6670e817dd39f61816e1e6e_l3.png)
次に、親配列の下のすべての数値を 0 にする必要があります。
したがって、行操作を実行して、最初の列の最後の 2 つの要素を置き換えます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+2f_1} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-87853177b6be449178c24e414dc0865a_l3.png)
次に、2 番目の列の最後の要素をゼロに変換します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+8f_2} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c4105ceb64b201c532109f8639bdefde_l3.png)
主対角線より下のすべての数値が 0 になると、連立方程式を解くことができます。これを行うには、行列を未知数を含む連立方程式の形式で再度表現します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39\end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 2x+3y+1z=-1 \\[2ex] -5y+z=3 \\[2ex] 13z=39 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-faae83295a3f7b3d8b6d76f78d56fac6_l3.png)
そして方程式の未知数を下から上に解きます。まず最後の方程式を解きます。
![]()
![]()
次に、z の値を 2 番目の方程式に代入して、y の値を求めます。
![]()
![]()
![]()
![]()
そして、最初の方程式でも同じことを行います。他の未知数の値を代入し、x を解きます。
![]()
![]()
![]()
![]()
![]()
したがって、連立方程式の解は次のようになります。
![]()
演習 4
ガウス法を使用して、3 つの未知数を含む次の連立方程式を解きます。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b005b2eda0d63c7130f2f5531c2ae4a0_l3.png)
ガウスの方法を適用する前に、すべての未知数が方程式の左側にあり、数値が右側にあるように連立方程式を整理する必要があります。
![Rendered by QuickLaTeX.com \left. \begin{array}{r}2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\} \longrightarrow \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6\end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1e0ca77b625e8f9e235ce8da4e4008df_l3.png)
システムが注文されたら、システムの開発されたマトリックスを構築します。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b88e3ff141b847028a55ba4b46b8e870_l3.png)
最初の行の数値はすべて偶数なので、行を操作する前に最初の行を 2 で割ります。これにより計算が簡単になるため、次のようになります。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1/2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b05235526cd8e44c16749606bfe8976c_l3.png)
次に、メイン配列の下のすべての数値を 0 にする必要があります。
したがって、行操作を実行して、最初の列の最後の 2 つの要素を置き換えます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3da82815d14fdfae0f61a8e1747fb9fe_l3.png)
前と同様、最後の行の数値はすべて 9 の倍数なので、計算を簡単にするために 9 で割ります。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex]\xrightarrow{f_3/9} & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-342000d19a7bd19e055a39695c79cb49_l3.png)
次に、2 番目の列の最後の要素をゼロに変換します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2158e7f439f677617bb8a40695fb5711_l3.png)
主対角線より下のすべての数値が 0 になると、連立方程式を解くことができます。これを行うには、行列を未知数を含む連立方程式の形式で再度表現します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x-2y-3z=3 \\[2ex] 5y+6z=-8 \\[2ex] 1z=2 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ea162e98aa70f8d56ffba28438a9de2a_l3.png)
そして方程式の未知数を下から上に解きます。まず最後の方程式を解きます。
![]()
![]()
次に、z の値を 2 番目の方程式に代入して、y の値を求めます。
![]()
![]()
![]()
![]()
![]()
そして、最初の方程式でも同じことを行います。他の未知数の値を代入し、x を解きます。
![]()
![]()
![]()
![]()
したがって、連立方程式の解は次のようになります。
![]()