コプレーナ線路

このページでは、2 本の線が同一平面上にある場合の意味がわかります。また、2 つの線路が同一平面上にある場合を確認することができ、さらに、同一平面上にある線路の例と演習問題も見つかります。

2本のコプレーナ線路とは何ですか?

解析幾何学におけるコプレーナ線の定義は次のとおりです。

2 本の線が同じ平面上にある場合、それらは同一平面上にあります。したがって、コプレーナ ラインは、割線、平行線、または一致線のみにすることができます。

さらに、平面を完全に定義するには、2 本のコプレーナ線で十分です。明らかに 1 つの平面に 2 本以上のコプレーナ線を含めることができますが、実際には、すべての平面に無限の数の線が含まれています。

一方、2 つの線が同一平面上にない場合は、それらが交差していることを意味します。

コプレーナ線路の例

コプレーナ線の概念をよりよく理解できるように、3 つの線を使用した例を次に示します。

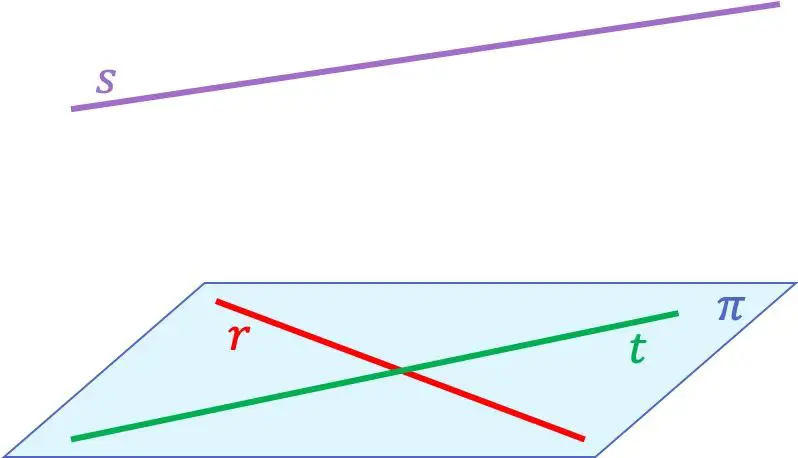
この場合、行は

そして

これらは同じ平面に属しているため、同一平面上にあります。その代わりに直線は

他の 2 つの線と交差しているため、どの線とも同一平面上にありません

そして

2 本の線が同一平面上にあるかどうかはどうやってわかりますか?

上のコプレーナ線の説明で見たように、コプレーナ線は割線、平行線、または一致線のみにすることができます。言い換えれば、2 つの交差する線は決して同一平面上にはなりません。

したがって、2 本の線が同一平面上にあるかどうかを知るには、それらの間の相対位置を決定する必要があります。2 本の交差する、平行な、または一致する線である場合、これはそれらが同一平面上にある線であることを意味します。

したがって、2 つのラインの同一平面性を確認するには、まず空間内の 2 つのラインの相対位置を計算する方法を知っておく必要があります。この概念にまだ慣れていない場合は、最初にリンクを参照することをお勧めします。そこには、完全な説明、例、演習、および解決された問題が記載されています。

コプレーナ線路の課題解決

例として、コプレーナ線路に関する典型的な演習を解いてみます。

• 次の 2 つの線が同一平面上にあるかどうかを判断します。

最初に行う必要があるのは、2 つの直線間の相対位置を見つけることです。そのためには、両方を同じタイプの方程式で表現する必要があります。それでは直線を越えます

一般 (または暗黙的な) 方程式からパラメトリック方程式へ:

したがって、各ラインの方向ベクトルは次のようになります。

2 つの線の方向ベクトルの座標は比例するため、一致する線または平行な線のみになります。したがって、この特定のケースでは、平行線と一致線は同一平面上にある線であるため、正確な相対位置を計算する必要はありません。したがって、 2 つの線は同一平面上にあります。