このセクションでは、ガウス・ジョルダン法によって連立方程式を論じて解く方法を見ていきます。つまり、確定互換システム (DCS)、不確定互換システム (ICS)、または非互換システムであるかどうかを判断します。さらに、演習を行って概念を完全に理解できるように、例と解決済みの演習が用意されています。
次に説明する内容を理解するには、 ガウス法を使用してシステムを解く方法をすでに知っていることが重要なので、先に進む前に目を通しておくことをお勧めします。
ガウス法により決定される互換性のあるシステム
ガウス行列の最後の行が
![]()
、 なれ
![]()
そして
![]()
任意の 2 つの数字、これはSCD (システム互換性決定済み) です。したがって、このシステムには独自のソリューションがあります。
大多数のシステムは SCD です。
例:
たとえば、次のようなシステムがあります。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bab5d5823e45833aa691a3510a2a23eb_l3.png)
展開された行列は次のとおりです。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}} \ \longrightarrow \ \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f8daea11edeedfd6b86bb251fe19032_l3.png)
このシステムを解くには、行列の行を操作し、主対角より下のすべての要素を 0 に変換する必要があります。 したがって、2 行目から 1 行目を減算し、3 行目から 2 を乗じた最初の行を減算します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3 -2f_1} & \end{array} \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d68ac25745ddc71d1e7f55f68dd4ea7a_l3.png)
主対角線の下のすべての数値が 0 になったら、システムを方程式形式に渡します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 6y+2z=0\\[2ex] 1z=-3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4457f1b034e72c6945bfe609eff52b9a_l3.png)
したがって、行列がシフトされ、最後の行が次のタイプであるため、このシステムはSCDです。
![]()
。したがって、いつものように、方程式から未知数をボトムアップで排除することによって、この問題を解決します。
![]()
![]()
![]()
z がわかったので、その値を 2 番目の方程式に代入して、次の値を求めます。
![]()
:
![]()
![]()
![]()
![]()
![]()
そして最後に、最初の方程式で同じことを行います。他の未知数の値を代入して、次のように解きます。
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
したがって、連立方程式の解は次のようになります。
![]()
ガウス法による互換性のないシステム
ガウス行列に 3 つの 0 が連続する行と 1 つの数字がある場合
![]()
、それはIS (互換性のないシステム) であるため、システムには解決策がありません。
例:
たとえば、システムのガウス行列を操作した後、次の結果が残ると想像してください。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & 1 & -1 & 0 \\[2ex] 0 & 3 & 1 & -1 \\[2ex] 0 & 0 & 0 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-defe65fa616eff800314ebc6dc6f552b_l3.png)
最後の行にあるように、
![]()
つまり、3 つの 0 と最後に数字が続くものはIF (互換性のないシステム) であるため、システムには解決策がありません。
知る必要はありませんが、解決策がない理由を以下に示します。
最後の行を取ると、次の方程式が得られます。
![]()
z の値がどのようなものであっても、それに 0 を掛けても 2 にはならないため、この方程式は決して満たされません (数値に 0 を掛けても常に 0 になります)。そして、この方程式が満たされることは決してないので、システムには解がありません。
ガウス法では互換性のあるシステムが不明
ガウス行列の行が 0 で埋められるたびに
![]()
、それはSCI (Indeterminate Compatibility System) であるため、システムには無限の解があります。
ICS を解決する方法の例を見てみましょう。
例:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a63dfebc1f23923714e475aad2e808_l3.png)
いつものように、最初にシステムの拡張行列を作成します。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\} \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f273040101827fdfea5c9a4858be5567_l3.png)
ここで、主対角線より下のすべての数値を 0 にしたいとします。そこで、最初の行に -2 を掛けた値を 2 番目の行に追加します。
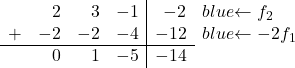
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c889a6f147c6b0430731aa778121af52_l3.png)
3 を 0 に変換するには、3 行目に -3 を乗算した最初の行を追加します。
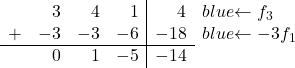
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5acccc51108267fef6d3320068743aa_l3.png)
最後の行の 1 を 0 に変換するには、3 行目に 2 行目に -1 を乗算した値を追加します。

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a02e4819adfbe7b80d2952f87f113757_l3.png)
最後の行はすべて 0 なので、削除できます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6aea469dceab08e6aa62571922eb2824_l3.png)
行全体が 0 で埋められているため、これはSCI です。
したがって、最終的には次のようなシステムになります。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y+2z=6 \\[2ex] y-5z=-14 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-598c031f4cba5a865952a57ed46f0f95_l3.png)
システムが SCI の場合、未知のパラメータからパラメータの値を取得する必要があります。
![]()
。そして、このパラメータに基づいてシステムを解く必要があります
![]()
。
したがって、次の値を割り当てます。
![]()
zへ:
![]()
の値を取得するために他の未知のものを選択することもできますが、
![]()
。
次に、2 番目の方程式からy を分離し、それを次の関数とします。
![]()
:
![]()
![]()
![]()
そして最後に、最初の方程式からxを削除し、それを次の関数として残します。
![]()
:
![]()
![]()
![]()
![]()
したがって、システム ソリューションは次のとおりです。
![]()
ご覧のとおり、システムが SCI の場合、パラメーターに応じてソリューションを残します。
![]()
。そして、それが取る値に応じて無限の解があることを覚えておいてください。
![]()
、解決策はどちらかになります。
解決済みの演習に進む前に、この記事ではガウスの方法を使用していますが、連立一次方程式を議論して解く別の方法がルーシュの定理であることを知っておく必要があります。実際にはもっと使われていると思われます。
ガウス・ジョルダン法を使用した方程式系の議論のための解決された演習
演習 1
関係するシステムのタイプを特定し、ガウス法を使用して次の方程式系を解きます。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be4ba1bd1ce7452e66c5189d995d948c_l3.png)
最初に行う必要があるのは、システムの拡張行列です。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex] 3 & 3 & 6 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b600f3fc0d79a06eb972dbacb673a780_l3.png)
次に、メイン配列の下のすべての数値を 0 にする必要があります。
したがって、行演算を実行して、最初の列の最後の 2 つの項をキャンセルします。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex]3 & 3 & 6 & 9 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_1} \\[2ex] \xrightarrow{f_3 - 3f_1}& \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & 1 & -4 \\[2ex] 0 & 0 & 0 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1d832d5bb115666614ae96822c360eb_l3.png)
3 つの 0 とそれに続く数字で構成される行列の行を取得しました。したがって、これはIS (互換性のないシステム) であり、システムには解決策がありません。
演習 2
システムのタイプを特定し、ガウス法を使用して次の方程式系の解を求めます。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f5aba495f2c6a301e923ee3c6238012_l3.png)
最初に行う必要があるのは、システムの拡張行列です。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bb5e5ab85946bddad72067fe17d937_l3.png)
次に、メイン配列の下のすべての数値を 0 にする必要があります。
したがって、行演算を実行して、最初の列の最後の 2 つの項をキャンセルします。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 2f_1} \\[2ex] \xrightarrow{f_3 + f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e48becaaa6683719ac57eb7d118943_l3.png)
次に、2 番目の列から最後の要素を削除してみましょう。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-16a1afc0eb224ee5f05c9e313586854d_l3.png)
しかし、0 が連続して表示されます。つまり、これはSCIであり、システムには無限に多くの解決策があります。
しかし、ICS なので、次のように系を解くことができます。
![]()
。したがって、0 行を削除します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c838c5f1b229d4c8a43ac9ddd8e3629_l3.png)
ここで、未知数を含む連立方程式の形式で行列を表現します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-2y+3z=1 \\[2ex] 1y+5z=7 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3fd941d33fec646d16b8181430c9986_l3.png)
の値を与えます
![]()
のために
![]()
![]()
の値を置き換えます
![]()
2 番目の方程式で次の値を求めます。
![]()
![]()
![]()
![]()
そして、最初の方程式でも同じことを行います。他の未知数の値を代入し、消去します。
![]()
![]()
![]()
![]()
![]()
したがって、連立方程式の解は次のようになります。
![]()
演習 3
それがどのようなタイプのシステムであるかを調べて、次の連立方程式をガウス法で解きます。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b04370b42854e53c650ca0eae14aadb5_l3.png)
最初に行う必要があるのは、システムの拡張行列です。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff2c7644e19fdf405f3c5c42ffc0ee98_l3.png)
ガウス法を適用するには、最初の行の最初の数値が 1 であれば簡単です。したがって、1 行目と 2 行目の順序を変更します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 \rightarrow f_2} \\[2ex] \xrightarrow{f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-471d89605d4bf6ddef1896a8fbe4c5ea_l3.png)
次に、メイン配列の下のすべての数値を 0 にする必要があります。
したがって、行演算を実行して、最初の列の最後の 2 つの項をキャンセルします。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 4f_1} \\[2ex] \xrightarrow{f_3 -f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4d5cbc50b87927077018175c4678e90_l3.png)
次に、2 番目の列の最後の要素をゼロに変換します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{8f_3 + f_2} \end{array} \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9013720883fd719e2bd0779bfbaa7a9f_l3.png)
行列をシフトすることができ、最後の行が次のタイプであるため、このシステムはSCDです。
![]()
。したがって、独自のソリューションになります。
主対角線より下のすべての数値が 0 になると、連立方程式を解くことができます。これを行うには、行列を未知数を含む連立方程式の形式で再度表現します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+1z=2 \\[2ex] -16y-3z=-12 \\[2ex] 5z=20 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f0433738d5d0a22bdd3b04dbd44fd1e_l3.png)
そして方程式の未知数を下から上に解きます。まず最後の方程式を解きます。
![]()
![]()
次に、z の値を 2 番目の方程式に代入して、y の値を求めます。
![]()
![]()
![]()
![]()
![]()
そして、最初の方程式でも同じことを行います。他の未知数の値を代入し、x を解きます。
![]()
![]()
![]()
![]()
したがって、連立方程式の解は次のようになります。
![]()
演習 4
システムのタイプを決定し、ガウス法で次の連立方程式を解きます。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e8a133547b4719d7833a792550fd322_l3.png)
最初に行う必要があるのは、システムの拡張行列です。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc41f78456a922a0fbff419d336b0b46_l3.png)
次に、メイン配列の下のすべての数値を 0 にする必要があります。
したがって、行演算を実行して、最初の列の最後の 2 つの項をキャンセルします。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 3f_1} \\[2ex] \xrightarrow{f_3 + 2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff92912f653c6aca7ceb7c990c9635a3_l3.png)
次に、2 番目の列から最後の要素を削除してみましょう。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c6904a64a721f3a92bef8c6b7d713cf_l3.png)
しかし、0 が連続して表示されます。つまり、これはSCIであり、システムには無限に多くの解決策があります。
しかし、ICS なので、次のように系を解くことができます。
![]()
。したがって、0 行を削除します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d856e2c1246f3629d68a7bcd3cd759a_l3.png)
ここで、未知数を含む連立方程式の形式で行列を表現します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-1y+4z=2 \\[2ex] -6y+15z=13 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4cf1265bfc12f94580de183230c8b7c_l3.png)
の値を与えます
![]()
のために
![]()
![]()
の値を置き換えます
![]()
2 番目の方程式で次の値を求めます。
![]()
![]()
![]()
![]()
![]()
そして、最初の方程式でも同じことを行います。他の未知数の値を代入し、消去します。
![]()
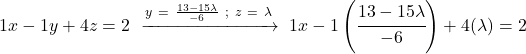
![]()
![]()
分数を含む合計があります。したがって、すべての項を共通の分母に還元します。
![]()
![]()
それらはすべて同じ分母を持つため、それらを 1 つの分数にグループ化できます。
![]()
そして最後に分子を操作します。
![]()
![]()
したがって、連立方程式の解は次のようになります。
![]()