正則行列または可逆行列

このページでは、正則行列または可逆行列の説明と、行列の逆行列がいつ実行できるか、いつ実行できないかを知る方法について説明します。さらに、概念を完全に理解するために正則行列の例もいくつか示し、最後にこのタイプの行列のすべてのプロパティを示します。

正則行列とは何ですか?

正則行列の定義は次のとおりです。

正則行列は、反転可能な正方行列です。つまり、前記行列の逆行列を計算できます。したがって、その行列式は非ゼロ (0) です。

通常の行列は、可逆行列、非特異行列、または非縮退行列とも呼ばれます。

通常の行列の反対の行列は、特異行列または縮退行列です。

したがって、行列が正則か特異かを知るには、つまり行列が可逆かどうかを知るには、行列の行列式を解くだけで十分です。

行列の行列式がゼロ以外の場合、行列は正則または可逆行列です。

行列の行列式がゼロに等しい場合、行列は特異であるか、可逆的ではありません。

結論として、行列の行列式を計算することは、行列に逆行列があるかどうかを知る最も簡単な方法であるため、行列の可逆性を判断するにはこれをお勧めします。

行列を逆にする方法を知りたい場合は、逆行列の公式を参照してください。行列を逆にする方法を段階的に説明しており、いくつかの例と練習用の解決済み演習も見つかります。

正則行列または可逆行列の例

正則行列または可逆行列の意味を理解したら、さまざまな次元の正則行列の例をいくつか見てみましょう。

通常または可逆 2×2 行列の例

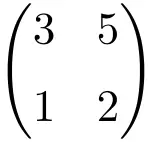
行列式を計算することで、それが正則行列であることを確認できます。

$\displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}$

2 次行列の行列式は 0 とは異なるため、正則行列になります。

通常または可逆 3×3 行列の例

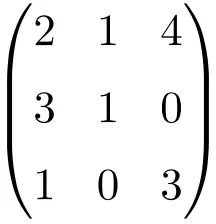
行列の行列式を作成して、それが可逆行列であることを確認する必要があります。

$\displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}$

次数 3 の行列の行列式は 0 以外の結果を与えるため、通常の行列になります。

通常または可逆の 4×4 行列の例

行列の行列式を取得すると、それが正則行列であることがわかります。

$\displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}$

次数 4 の行列の行列式はゼロではないため、可逆行列です。

警告:行列式の計算に疑問がある場合は、行列式の計算方法のページを参照してください。

正則行列または可逆行列のプロパティ

正則行列または可逆行列は線形代数にとって非常に重要であり、これは次の特性によるものです。

A が可逆行列の場合、その転置行列または転置行列も同様です。さらに、転置の逆行列は逆行列の転置と等しくなります。

$\displaystyle \left(A^t\right)^{-1}=\left(A^{-1}\right)^t$

通常の行列の範囲は常に可能な最大値です。つまり、範囲は行列の次元に相当します。

2 つの可逆行列間の行列積により、別の通常の行列が生成されます。この条件は、行列式のプロパティを使用して簡単に証明できます。

$\displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0$

すべての直交行列は同時に正則行列でもあります。

連立一次方程式を表す行列を A とします。
$(Ax=b)$

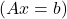
、 A が正則行列の場合、システムは一意の解を持ち、したがって互換性のある行列式システム (SCD) になります。

また、系が均一系であれば、
$(Ax=0)$

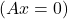
そして A を反転できる場合、システムの解は自明です。

$x=0.$

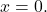
通常の行列の列と行は互いに線形に独立しています。

正規行列または可逆行列のすべての固有値 (または固有値) は非ゼロです。

通常のゴールドの可逆マトリックス

正則行列とは何ですか?