このページでは、線形独立ベクトルと線形依存ベクトルとは何かについて説明します。また、ベクトルのセットが線形依存しているか独立しているかを判断する方法の例も表示されます。さらに、線形独立性と依存性に関する演習と解決された問題が段階的に見つかります。
線形独立ベクトルとは何ですか?
自由ベクトルのセットは、いずれも他のベクトルの線形結合として記述できない場合、線形独立です。
言い換えれば、ベクトルのセットが与えられると、
![]()
次の方程式の唯一の解がある場合、これらは線形独立です。
![]()
これらはすべて係数です
![]()
0に等しい:
![]()
幾何学的には、2 つのベクトルが同じ方向を持たない場合、つまり平行でない場合、2 つのベクトルは線形独立です。
簡潔にするために、これらを LI ベクトルであると直接言うこともあります。または、ベクトルが線形独立性を持っていること。
線形従属ベクトルとは何ですか?
明らかに、線形依存ベクトルは線形独立ベクトルの逆を意味します。したがって、その定義は次のようになります。
平面の自由ベクトルのセットは、それらのいずれかがシステムを形成する他のベクトルの線形結合として表現できる場合、線形依存します。
言い換えれば、ベクトルのセットが与えられると、
![]()
次の方程式の解が存在する場合、これらは線形に依存します。
![]()
ある係数を持つもの
![]()
0とは異なります:
![]()
逆も同様です。ベクトルが他のベクトルの線形結合である場合、セット内のすべてのベクトルは線形従属になります。
さらに、2 つのベクトルが平行である場合、これはそれらが線形に依存していることを意味します。
略して単に LD ベクトルと呼ばれることもあります。あるいは、ベクトルに線形依存性があることさえあります。
ベクトルが線形従属か独立かを知る方法の例
次に、線形依存ベクトルと独立ベクトルの典型的な例を見ていきます。
- 次の 3 つの 3 次元ベクトルに線形依存性があるか独立性があるかを判断します。
![]()
![]()
![]()
まず、線形結合条件を示す必要があります。
![]()
ここで、各ベクトルをその座標に置き換えます。ゼロと同様、ゼロ ベクトルに対応します。
![]()
係数はベクトルを乗算するため、次の式は等価です。
![]()
ベクトルを追加します。
![]()
よく見ると、左ベクトルの各座標は右ベクトルの各座標に等しくなければならないため、前の式は 3 つの方程式に対応しています。したがって、3 つの未知数を含む 3 つの方程式からなる同次系が得られます。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1-2a_2+4a_3 = 0 \\[2ex] 5a_1+3a_2+2a_3 =0\\[2ex] 2a_1-a_2+a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c6bb8117dd8ae715314efe73fe65eed8_l3.png)
したがって、私たちがしなければならない唯一のことは、未知数が次のような連立方程式を解くことです。
![]()
そして
![]()
これを行うには、任意の方法 (置換法、ガウス法、クラマー規則など) を使用できます。ただし、ベクトルが LI か LD かを知るには、自明な解 (すべての係数がゼロに等しい) 以外の解が存在するかどうかを判断するだけで十分です。それで:
- ベクトルの成分で構成される行列の行列式がゼロではない場合、これは方程式系の解が 1 つだけであることを意味します (
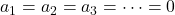
) したがって、ベクトルは線形独立です。
- 一方、ベクトルの成分で構成される行列の行列式がゼロに等しい場合、これは連立方程式に複数の解があり、したがってベクトルが線形依存していることを意味します。
したがって、計算する必要があるのは、ベクトルの座標による行列式だけです (3×3 の行列式なので、Sarrus の法則で解決できます)。この行列式は、前の連立方程式の係数に対応します。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&-2&4\\[1.1ex] 5&3&2 \\[1.1ex] 2&-1&1 \end{vmatrix} = -37 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-046e05ff603822985510c7bdc8b73021_l3.png)
この場合、行列式は 0 ではないため、ベクトルは線形独立です。
したがって、連立方程式の可能な唯一の解は、すべての未知数がゼロに等しい自明な解です。
![]()
線形依存ベクトルと独立ベクトルのプロパティ
ベクトルの線形依存性または独立性には次の特徴があります。
- 2 つの比例ベクトルは平行であり、方向が同じであるため線形に依存します。
- 同様に、2 つのベクトルが同じ方向を持たない場合、または比例しない場合、それらは線形独立です。
- 3 つの共面ベクトル (同じ平面内にある) は線形に独立しています。
- ヌルベクトル
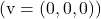
は任意のベクトルに線形依存します。
- 線形独立ベクトルのセットはベクトル空間を生成し、ベクトル基底を形成します。 3 つのベクトルが垂直であれば、それは直交基底です。そして、モジュールも 1 に等しい場合、これは正規直交基底に対応します。
線形依存性と独立性の演習を解決しました
以下に、線形依存ベクトルと独立ベクトルに関する演習をいくつか用意しています。
演習 1
次のベクトルが線形依存しているか独立しているかを判断します。
![]()
![]()
![]()
まず、線形結合条件を設定します。
![]()
![]()
![]()
![]()
前述の等式は、次の線形方程式系に対応します。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1+2a_2+5a_3 = 0 \\[2ex] -2a_1+a_2-a_3 =0\\[2ex] a_1+3a_2+a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-58f1b449f48096570437df0ca40f8a8d_l3.png)
方程式系を述べたら、その項を使用して行列の行列式を解きます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&2&5\\[1.1ex] -2&1&-1 \\[1.1ex] 1&3&1 \end{vmatrix} = -29 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-caa6d4f135e79bb8b6d2368ff7eebefb_l3.png)
この場合、行列式は 0 ではないため、3 つのベクトルは互いに線形独立です。
演習 2
次のベクトルを線形依存または独立として分類します。
![]()
![]()
![]()
まず第一に、線形結合の方程式を立てます。
![]()
![]()
![]()
![]()
前の等式から、次の均一方程式系が得られます。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1-2a_2+3a_3= 0 \\[2ex] 4a_1-a_3 =0\\[2ex] 3a_1+2a_2-4a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c94610b6f8baef34a1fb4601c148f515_l3.png)
方程式系を述べたら、ベクトルの座標を使用して行列の行列式を解きます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&-2&3\\[1.1ex] 4&0&-1 \\[1.1ex] 3&2&-4 \end{vmatrix} \bm{= 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-67678c37fdaf0955ef8bbab8d34379f8_l3.png)
この場合、行列式は 0 に相当するため、3 つのベクトルは互いに線形に依存します。
演習 3
次の 3 つのベクトルについて、どのベクトルのペアが線形依存し、どのペアが線形独立であるかを示します。
![]()
ベクトルのペアが線形依存しているか独立しているかを判断する最も簡単な方法は、それらが比例しているかどうかを確認することです。
まずベクトルを確認します
![]()
ベクトルを使って
![]()
![]()
次に、ベクトルを確認します。
![]()
ベクトルを使って
![]()
![]()
最後に、ベクトルをテストします。
![]()
ベクトルを使って
![]()
![]()
したがって、相互に線形に依存する唯一のベクトルのペアは、
![]()
そして
![]()
さらに、それらの関係は次のとおりです。
![]()
または同等のもの:
![]()
一方、他のベクトルのペアは線形独立です。
演習 4
次の 4 つのベクトルの相互の線形依存性または独立性を調べます。
![]()
![]()
![]()
![]()
まず、線形結合条件を設定します。
![]()
![]()
![]()
![]()
この場合、4 つの未知数を含む 3 つの方程式からなる系があります。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} -a_2+4a_3-2a_4 = 0 \\[2ex] a_1-2a_2+a_3-3a_4 =0\\[2ex] 2a_1-a_3+2a_4 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e9451263e5a31994569292e32666d93e_l3.png)
正方行列しか決定できないため、システム行列全体の行列式を解くことはできません。したがって、3×3 行列式の考えられるすべての組み合わせを計算し、それらの 1 つが 0 に等しいかどうかを確認する必要があります。その場合、ベクトルは線形依存します。一方、すべての行列式が 0 と異なる場合、4 つのベクトルは次のようになります。線形独立であること。
係数の行列式を計算します
![]()
そして
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0&-1&4\\[1.1ex] 1&-2&1 \\[1.1ex] 2&0&-1 \end{vmatrix} =13\bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-488d7848a40aa9a91bd5b3aa1f09b774_l3.png)
最初の 3 つの係数 (または最初の 3 つのベクトル) の行列式はゼロではありません。そこで、係数の行列式を試してみます。
![]()
そして
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0&-1&-2\\[1.1ex] 1&-2&-3 \\[1.1ex] 2&0&2 \end{vmatrix} \bm{= 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1475a77f10ea0c16147a6f9c3f611b4_l3.png)
ゼロ行列式が得られました。4 つのベクトルが線形に依存していることがすでにわかっているため、他の行列式を計算する必要はありません。
演習 5
の値を計算します
![]()
したがって、次のベクトルは線形独立です。
![]()
![]()
![]()
まず第一に、線形結合の方程式を立てます。
![]()
![]()
![]()
![]()
前のベクトル方程式から、次の均一方程式系が得られます。
![Rendered by QuickLaTeX.com \left. \begin{array}{l}3a_1-2a_2+a_3= 0 \\[2ex] -a_1+4a_2+3a_3 =0\\[2ex] 5a_1+7a_2+ka_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-16f88cbf406c1faf61307b99179a5de6_l3.png)
方程式系を述べたら、その系の行列式を解いてみましょう。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3&-2&1\\[1.1ex] -1&4&3 \\[1.1ex] 5&7&k \end{vmatrix} =10k-120](https://mathority.org/wp-content/ql-cache/quicklatex.com-d748080bb1cacc1c80a35ef633a2d85e_l3.png)
このステートメントは、ベクトルが線形依存している必要があることを示しています。したがって、行列式はゼロに等しくなければなりません。
![]()
![]()
![]()
![]()
したがって、ベクトルが線形依存性を持つように、定数は 12 に等しくなければなりません。