完全二乗三項式

9月 17, 2023

このページでは、完全二乗三項式とは何か、およびそれがどのように計算されるかを説明します。さらに、いくつかの例を確認し、ステップバイステップの完全二乗三項演習で練習することができます。

完全二乗三項式とは何ですか?

明らかに、完全二乗三項式の意味を確認する前に、三項式とは何かを知る必要があります。そのため、続行する前に、このリンク先のページ (詳細が説明されています) を参照することをお勧めします。

したがって、完全二乗三項式の定義は次のようになります。

数学では、完全二乗三項式( TCPとも呼ばれます) は、二項式を二乗することによって得られる三項式です。

したがって、完全平方三項式は、2 つの完全平方を含む多項式と、これらの平方の底の 2 倍の積である別の項で構成されます。

完全二乗三項式

上の 2 つの公式からわかるように、完全二乗三項式は 2 つの注目すべきアイデンティティ (または注目すべき製品) から得られるため、これが非常に重要です。具体的には、完全二乗三項式は、加算の二乗または減算の二乗を解くときに見つかります。

完全二乗三項式の例

完全二乗三項式の概念を理解するために、2 つの例を段階的に説明します。

例1

$x^2+6x+9$

この例は、代数式に 2 つの完全二乗 (つまり、正確な平方根がある) があるため、完全二乗三項式です。

$x^2$

と 9 は次と同等です

$x$

と 3 をそれぞれ 2 乗します。

$(x)^2 = x^2$

$(3)^2 = 9$

さらに、三項式の最後に残った項

$(6x)$

これは、前の 2 つの正方形の底を 2 で乗算することで得られます。

$2\cdot x \cdot 3 = 6x$

したがって、この演習で注目すべき完全なアイデンティティは次のようになります。

$(x+3)^2 =x^2+6x+9$

例 2

$16x^2-40x+25$

この他の例も、3 つの必要な条件が満たされているため、完全平方三項式です。つまり、2 つの項は 2 つの完全平方に対応し、別の項はこれらの平方の底を互いに乗算して 2 を掛けた結果です。

$(4x)^2 = 16x^2$

$(5)^2 = 25$

$2\cdot 4x \cdot 5 =40x$

この場合、完全二乗三項式は負の単項式を持つため、二乗差の顕著な等式の展開に対応します。

$(4x-5)^2 = 16x^2-40x+25$

完全平方三項式を因数分解する方法

代数学では、完全二乗三項式 (PCT) の因数分解が非常に一般的な問題です。それが何を意味するかわからない場合のために説明しますが、多項式の因数分解とは、その式を因数の積に変換することを意味します。

したがって、このタイプの代数三項式を因数分解するには、次の規則に従う必要があります。

三項式には 2 つの完全平方が必要です。これを次のように呼びます。
$a^2$

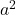
そして

$b^2.$
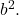
三項式の残りの 3 番目の項は、2 つの完全平方の底の 2 倍の積に等しくなければなりません。これは数学的には次の式に対応します。
$2\cdot a \cdot b.$
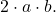
因数分解された三項式は次のようになります。
$(a+b)^2$

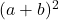
完全平方三項式のすべての項が正の場合、そうでない場合、平方根の 2 倍積が負の符号を持つ場合、因数分解された三項式は次のようになります。

$(a-b)^2.$

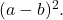
手順を理解するには、段階的に演習を解いていきます。

次の完全二乗三項式を因数分解します。

$x^2-12x+36$

最初に行う必要があるのは、三項式に完全な平方である 2 つの要素があるかどうか、つまり、その平方根が 10 進数を与えないかどうかを識別することです。この問題では

$x^2$

変数の二乗です

$x$

36 は 6 の 2 乗です。

$\sqrt{x^2} = x$

$\sqrt{36} = 6$

したがって、三項式には 2 つの完全平方があります。

次に、中間項が前のステップで計算された 2 つの根の 2 倍積に等しいかどうかを確認する必要があります。

$2 \cdot x \cdot 6 = 12x$

このルールも尊重されます。

その後、すべての条件が満たされます。したがって、因数分解された完全二乗三項式は、見つかった 2 つの根によって形成される二項式になります (

$x$

そして数字6) の二乗:

$x^2-12x+36=(x-6)^2$

中間項は負であるため、括弧内にマイナス記号を入れる必要があります。一方、それが正の場合は、合計を追加する必要があります。

$x^2+12x+36=(x+6)^2$

論理的には、因数分解は複雑な手順であるため、以下の演習に加えて、多項式の因数分解の例を参照することをお勧めします。このリンクでは、三項式だけでなく、あらゆるタイプの多項式を同様に迅速に因数分解するために使用される方法についても説明します。

完全二乗三項式の演習問題を解決しました

対応する式を適用して、次の三項式を正方形の二項式に変換します。

$\text{A)} \ x^2+8x+16$

$\text{B)} \ x^2-14x+49$

$\text{C)} \ x^4-20x^2+100$

$\text{D)} \ 81x^2+90x+25$

$\text{E)} \ 64x^4-176x+121$

解決策を見る

完全二乗三項式を二乗二項式の累乗に変換するには、和の二乗と差の二乗の注目すべき恒等式を表す次の式を使用する必要があります。

$(a+b)^2 = a^2+2ab+b^2$

$(a-b)^2 = a^2-2ab+b^2$

まだ：

$\text{A)} \ x^2+8x+16 = (x+4)^2$

$\text{B)} \ x^2-14x+49 = (x-7)^2$

$\text{C)} \ x^4-20x^2+100 = (x^2-10)^2$

$\text{D)} \ 81x^2+90x+25 = (9x+5)^2$

$\text{E)} \ 64x^4-176x+121 =\left( 8x^2-11)^2$

⬇⬇⬇ ご質問はすべてコメント欄に書き込んでいただけますので、お忘れなく！ ⬇⬇⬇

コメントする返信をキャンセル