このページでは、数値の多項式分解 (または式) を行う方法を説明します。ここでは、多項式分解の例を確認できるほか、段階的に解決された練習問題も見つかります。
数値の多項式分解とは何ですか?
数学における数値の多項式分解は、その数値を合計で表現することで構成されます。合計の各項は、数値の各桁の 10 を底とする累乗の積になります。
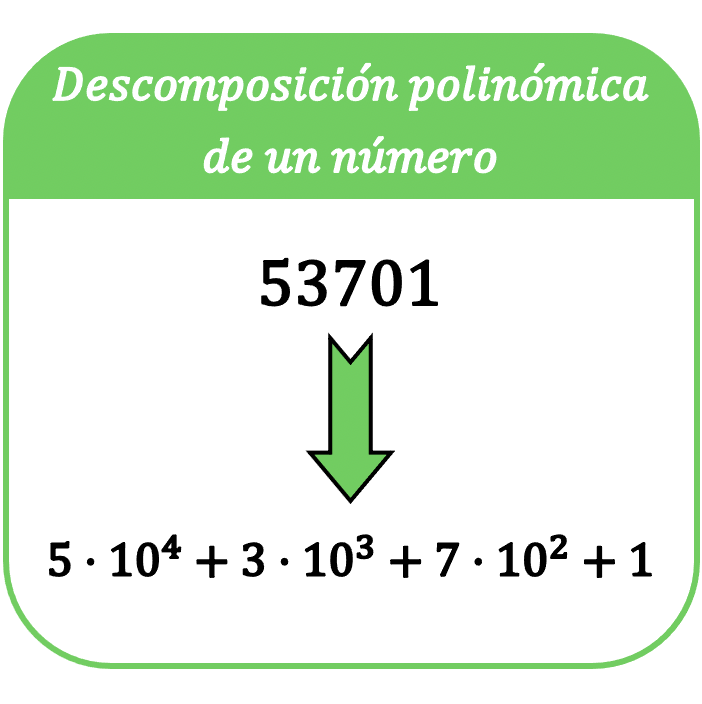
数値の多項式分解という用語は、数値の多項式表現としても知られています。
多項式分解を行う方法
数値の多項式分解を実行するには、数値の各桁に10 の右辺の桁数を乗算する必要があります。
たとえば、次の数値の多項式分解を計算したい場合:
![]()
この場合、数字の 8 は 5 番目の位置を占めているため、右側に 4 桁あります。したがって、8 に 10 の 4 乗を乗算する必要があります。
![]()
したがって、数値 86293 を多項式に分解するには、数値のすべての桁に対して同じことを行い、すべての乗算を合計の形式で表現する必要があります。
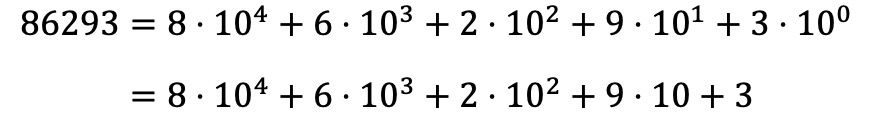
累乗 10 0が消えることに注意してください。累乗の性質によれば、0 に累乗した数値は 1 に等しいため、10 0 =1 となります。
一方、乗算分解から数値の多項式分解を求めることもできます。
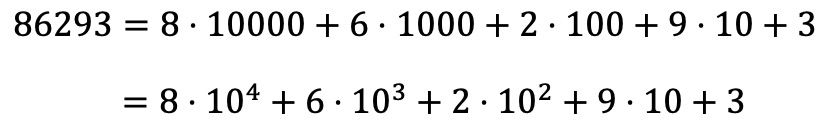
数値の多項式分解の例
数値の多項式分解がどのように実行されるかを確認したら、概念を完全に理解するためにこのタイプの演算のさまざまな例を見ていきます。
- 3641 の多項式分解:
![]()
- 56912 の多項式分解:
![]()
- 27084 の多項式分解:
![Rendered by QuickLaTeX.com \begin{aligned} 27084 &= 2\cdot 10^4 +7\cdot 10^3 +0\cdot 10^2 + 8\cdot 10 + 4 \\[2ex] & = 2\cdot 10^4 +7\cdot 10^3 + 8\cdot 10 + 4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f72230330ff9c9150dc9ab19a89a42d8_l3.png)
この最後の例では、数値にゼロを乗算すると相殺されるため、3 番目の乗算を単純化できます。
10 進数の多項式分解
自然数の多項式分解を実行する方法を見てきました。しかし…10 進数を多項式に分解するにはどうすればよいでしょうか?
さて、 10 進数の多項式分解は整数の場合と同じ方法で行われますが、さらに、10 進数の各桁に 10 を底とする累乗を掛けた積を加算します。その指数は、その数値が占める小数点以下の位置に負の値を付けたものになります。サイン。
これを言葉で説明すると非常に複雑に見えるかもしれませんが、例を使用するとよりよく理解できることがわかります。
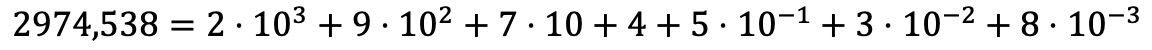
解決された多項式分解演習
多項式分解を練習できるように、段階的に解決するいくつかの演習を用意しました。
ご質問がございましたら、コメント欄からお問い合わせください。 🤔🤔🤔
演習 1
次の数値の多項式分解を実行します。
![]()
![]()
![]()
![]()
任意の数値の多項式分解を求めるには、その数値の各桁に右側の桁数を 10 倍し、すべての乗算を加算します。まだ:
![]()
![]()
![]()
![]()
演習 2
次の数値の多項式分解を求めます。
![]()
![]()
![]()
![]()
数値を多項式に分解するには、その数値の各桁にその右側の桁数を 10 倍し、すべての積を加算する必要があります。まだ:
![]()
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned} 3030 & = 3 \cdot 10^3+ 0\cdot 10^2 +3 \cdot 10 +0 \\[2ex] &= 3 \cdot 10^3+3 \cdot 10 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e3500d6a94685566b267e8708e8b0d7_l3.png)
![]()
![]()
演習 3
次の 10 進数の多項式分解を計算します。
![]()
![]()
![]()
![]()
この問題ではすべての数値が 10 進数であるため、これらを分解するには、次のようにして、10 進数以外の各桁に、その小数点までの桁数に累乗した 10 を乗算し、各 10 進数の桁に、その小数点以下の桁数に累乗した 10 を乗算する必要があります。マイナスのサイン。
![]()
![]()
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned} 0,82694 & = 0 + 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\\[2ex] & = 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-deb6b85265df2e98bcb5e116e19c397f_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned} 5,7201 & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+0\cdot 10^{-3}+1\cdot 10^{-4}\\[2ex] & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+1\cdot 10^{-4} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e204c24ba4f9138f503cf2c2a0e379d_l3.png)