このページでは、代数分数とは何か、それらが等しい場合、代数分数を簡略化する方法、および代数分数を使用した演算 (加算、減算、乗算、除算) を実行する方法について説明します。さらに、代数分数の段階的な演習を解くことができます。つまり、ここでは代数分数に関するすべてがわかります。
代数分数とは何ですか?
数学における代数分数は、分子に多項式、分母に別の多項式を持つ分数です。
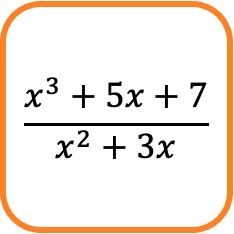
たとえば、上記の分数式は、分子と分母が多項式で構成されているため、代数的な分数で構成されます。
代数的な分数相当
代数の分数の定義がわかったら、そのような 2 つの分数が等しい場合を見てみましょう。
数学的には、次の条件が満たされる場合、2 つの代数分数は等価です。
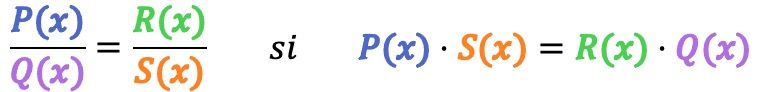
例として、次の 2 つの代数分数が等しいかどうかを確認します。
![]()
分数が代数的に等しいかどうかを判断するには、それらの項を横方向に乗算します。
![]()
次に、多項式の乗算を計算してみましょう。
![]()
![]()
方程式の両側で同じ式が得られたため、これらは実質的に 2 つの等価な代数分数になります。
代数分数を簡略化する
代数分数を単純化するには、まず多項式の分子と分母を因数分解し、次にそれらに共通する因数を除去する必要があります。
明らかに、代数分数を単純化するには、多項式因数分解とは何か、またそれがどのように行われるかを理解することが不可欠です。多項式の因数分解方法がまだわからない場合、または完全に覚えていない場合は、続行する前にリンク先のページにアクセスすることをお勧めします。 そうしないと、手順がほとんど理解できなくなります。多項式の因数分解方法を段階的に説明しており、さらにいくつかの例を見て、解決済みの演習で練習することができます。
ここで、例を使用して多項式の因数分解方法を適用することで代数分数がどのように簡略化されるかを見てみましょう。
- 次の代数分数を簡略化します。
![]()
まず、分数の分子と分母の多項式を因数分解します。
![]()
⬆(多項式がどのように因数分解されたかわからない場合は、上のリンクを参照してください)⬆
そして、多項式を因数分解したら、分子と分母の間の共通因数を削除します。つまり、繰り返される項をすべて削除します。
![]()
したがって、簡略化された代数分数は次のようになります。
![]()
この問題では、代数分数の多項式は根を求めることによって因数分解されました。ただし、場合によっては、共通因数を使用して多項式を直接因数分解できる場合があります (より高速な方法)。このリンクでは、多項式から共通因数を取得することが何を意味するのかを確認し、共通因数を使用して代数分数を簡略化する方法を説明します。
代数的な分数を使った演算
あらゆる種類の分数と同様に、代数的な分数を使用した演算も実行できます。具体的には、代数的な分数を加算、減算、乗算、除算することができます。以下では、各タイプの演算がどのように計算されるかを例を挙げて段階的に説明します。
代数的な分数の加算と減算
代数分数の加算と減算の手順は実質的に同じなので、一緒に解析します。最初に 2 つの代数分数を加算する例を見て、以下では代数分数を減算する方法の違いを調べます。
代数的な分数の加算
代数的な分数の加算は、通常の分数の場合と同じ方法で行われます。まず、分数を公分母に減らし、次に分子を加算します。
例を使用して、代数分数がどのように加算されるかを見てみましょう。
![]()
まず、分数の分母を因数分解します。
![]()
![]()
次に、分数を公分母に減らすために、分母のlcm (最小公倍数) を見つける必要があります。
ヒント:分母の lcm は、常に、共通の因数を最大の指数に乗じた積から、非共通の因数を乗算して形成されます。
たとえば、私たちの場合
![]()
分母を最大累乗した公約数は次のようになります。
![]()
そして、分母間の非共通因数は、
![]()
したがって、この場合の分母の lcm は次のようになります。
![]()
したがって、分母の lcm は次のようになります。
![]()
したがって、これは 2 つの分数の新しい分母になります。
![]()
共通分母を見つけたら、分子を変更する必要があります。これを行うには、通常の分数の加算と同じプロセスに従います。各分数について lcm を除算します。
![]()
元の分母とその結果を分子で乗算します。
![]()
![]()
![]()
2 つの分数は分母が同じなので、これらをまとめることができます。
![]()
最後に、分子を操作します。まず単項式と多項式の積を計算します。
![]()
![]()
次に、同様の項を分子に追加します。
![]()
通常はすでにそこに到達していますが、この問題を詳しく見ると、分子から共通因数を削除することで代数分数をさらに単純化できます。まだ:
![]()
![]()
![]()
したがって、2 つの代数分数の合計はすでに完成しています。
代数的な分数の減算
代数分数を減算するには、代数分数を加算する場合と同様の手順に従う必要があります。まず、分数を公分母に減算し、次に分子を減算します。
例を使用して、代数的な分数がどのように減算されるかを見てみましょう。
![]()
まず、2 つの分数の分母を因数分解する必要があります。
![]()
通常の分数の減算と同様に、分母のlcm (最小公倍数) を計算して、分数を公分母に減らす必要があります。この場合、分母の lcm は次のようになります。
![]()
したがって、これは 2 つの分数の新しい分母になります。
![]()
ここで、通常の分数を減算する場合と同じプロセスを適用します。各分数について lcm を除算します。
![]()
元の分母とその結果を分子で乗算します。
![]()
![]()

2 つの代数分数は分母が同じなので、これらを結合します。
![]()
そして分子を操作します。まず多項式の乗算を解きます。
![]()
代数の分数を引き算するときに非常によくある間違いは、この乗算を実行した後に括弧を入れるのを忘れることです。負の符号は最初の項だけでなく、積の結果として得られるすべての要素に影響を与えるため、これはエラーになります。
括弧内の操作を実行します。
![]()
したがって、負符号のおかげで、括弧内のすべての項の符号を変更します。
![]()
そして最後に、類似した単項式をグループ化します。
![]()
代数的な分数の乗算
代数的な分数を乗算するには、最初にその分数のすべての多項式を因数分解し、次に分子同士を乗算し、分母同士を乗算し、最後に得られた分数を単純化します。
したがって、代数的な分数の積は、実際には通常の分数の積と同じ方法で計算されます。
次に、例を使用して 2 つの代数分数を乗算する方法を見てみましょう。
![]()
まず最初に、分数のすべての多項式、分子と分母の両方を因数分解する必要があります。
![]()
では、分数の掛け算をしてみましょう。これを行うには、分子と分母を掛け合わせます。
![]()
![]()
最後に、分母と分子で繰り返される因子を単純化します。
![]()
したがって、乗算の結果は次のようになります。
![]()
分数をこれ以上単純化することはできません。したがって、代数的な分数の乗算はすでに完了しています。
代数的な分数の割り算
代数分数の割り算を計算するには、まずすべての多項式を因数分解し、次に分数を横方向に乗算し (最初の分子と 2 番目の分母、最初の分母と 2 番目の分子)、最後に代数分数を単純化します。
それでは、例を使用して 2 つの代数分数がどのように除算されるかを詳しく見てみましょう。
![]()
2 つの代数分数を除算する最初のステップは、演算に含まれるすべての多項式を因数分解することです。
![]()
次に、分数を割る必要があります。これを行うには、分数を横方向に乗算します。つまり、最初の分子に 2 番目の分母を乗算し、その結果が新しい分数の分子になります。また、同様に、最初の分母に 2 番目の分子を乗算します。結果は新しい分数の分母になります。
![]()
![]()
分母と分子で繰り返される因子を単純化します。
![]()
![]()
そして、分数をさらに単純化することができます。
![]()
![]()
分数をこれ以上単純化することはできません。したがって、代数的な分数はすでに分割されています。
代数分数の演習問題を解決しました
以下では、代数分数を段階的に解決するいくつかの演習を提供します。これにより、練習して概念を理解することができます。ご質問がございましたら、以下のコメント欄にご記入ください。 💬💬💬
演習 1
次の代数分数が等しいかどうかを判断します。
![]()
2 つの代数分数が等しいかどうかを確認するには、それらを横方向に乗算し、等しくなるかどうかを確認する必要があります。したがって、最初に最初と 2 番目の分数を確認します。
![]()
![]()
方程式の左側にある注目すべき恒等式を解きます。
![]()
✅
この場合、等号が得られたため、最初の分数と 2 番目の分数は代数的に等しいことになります。
同じ手順を最初と 3 番目の代数分数にも適用します。
![]()
![]()
![]()
![]()
❌
ただし、今回は代数的な分数が方程式を満たしていないため、最初と 3 番目の分数は数学的に異なります。
結論として、3 番目の分数は最初の分数とは異なり、したがって 1 番目と 2 番目の分数は等しいため、2 番目の分数とも等しくありません。
![]()
演習 2
次の代数分数を簡略化します。
![]()
![]()
![]()
![]()
代数分数を単純化するには、多項式の分子と分母を因数分解し、繰り返される因数を取り除く必要があります。まだ:
![Rendered by QuickLaTeX.com \text{A)} \ \begin{array}{l} \cfrac{5x^2+10x}{11x} =\cfrac{5x(x+2)}{11x} = \\[4ex] =\cfrac{5\cancel{x}(x+2)}{11\cancel{x}}= \cfrac{\bm{5(x+2)}}{\bm{11}}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3f06c8f3d861d237ca41232418bd3e17_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{array}{l} \cfrac{x^2-4}{x^2+2x-8} = \cfrac{(x-2)(x+2)}{(x-2)(x+4)}= \\[4ex] = \cfrac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}(x+4)}=\cfrac{\bm{x+2}}{\bm{x+4}}}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f9577181669de9b9760dfe7ed8425e17_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{array}{l} \cfrac{x^3-2x^2-3x}{x^2-3x} = \cfrac{x(x+1)(x-3)}{x(x-3)}}= \\[4ex] = \cfrac{\cancel{x} (x+1) \cancel{x-3}}{\cancel{x}\cancel{(x-3)}} = \cfrac{x+1}{1} = \\[4ex] = \bm{x+1}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04505e35cce382f2905db108961c6718_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{array}{l} \cfrac{x^3-3x+2}{x^3+4x^2+x-6}=\cfrac{(x-1)^2(x+2)}{(x-1)(x+3)(x+2)}= \\[4ex] = \cfrac{(x-1)^{\cancel{2}}\cancel{(x+2)}}{\cancel{(x-1)}(x+3)\cancel{(x+2)}}=\cfrac{\bm{x-1}}{\bm{x+3}}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-68ca63836b70d9aa6731e3271247d681_l3.png)
演習 3
次の代数分数の加算と減算を計算します。
![]()
![]()
![]()
![]()
代数的な分数を加算 (または減算) するには、まず分数を公分母に減算し、次に分子を加算 (または減算) する必要があります。それで:
![Rendered by QuickLaTeX.com \text{A)} \ \begin{array}{l} \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6} = \cfrac{4}{x(x+2)} + \cfrac{3x-2}{(x+2)(x-3)} = \\[4ex] =\cfrac{4\cdot(x-3)}{x(x+2)\cdot (x-3)} + \cfrac{(3x-2)\cdot x}{(x+2)(x-3)\cdot x} = \cfrac{4\cdot(x-3) + (3x-2)\cdot x}{x(x+2)(x-3)} = \\[4ex] = \cfrac{4x-12 + 3x^2-2x}{x(x+2)(x-3)} = \cfrac{ \bm{3x^2+2x-12}}{\bm{x(x+2)(x-3)}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6524d97070ae44570c7bbd75df0b6bb5_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{array}{l} \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4} = \cfrac{4x}{x(x+1)^2} - \cfrac{2}{(x+1)(x-4)}= \\[4ex] = \cfrac{4x \cdot (x-4)}{x(x+1)^2 \cdot (x-4)} - \cfrac{2 \cdot (x+1) \cdot x}{(x+1)^2(x-4)\cdot x}= \cfrac{4x \cdot (x-4) - 2 \cdot (x+1) \cdot x }{x(x+1)^2 (x-4) }= \\[4ex] = \cfrac{4x^2 -16x - 2 \cdot (x^2+x) }{x(x+1)^2 (x-4) }= \cfrac{4x^2 -16x - 2x^2 - 2x }{x(x+1)^2 (x-4) } =\\[4ex] =\cfrac{2x^2 -18x}{x(x+1)^2 (x-4)}=\cfrac{x(2x -18)}{x(x+1)^2 (x-4)}= \\[4ex] = \cfrac{\bm{2x -18}}{\bm{(x+1)^2 (x-4)}}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b228a6d7ced30d4dfdca7fa7653cec0e_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{array}{l}\cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}=\cfrac{7x}{(x-2)^2} + \cfrac{-5}{x-2}} = \\[4ex] = \cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)\cdot (x-2)}=\cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)^2}= \\[4ex] = \cfrac{7x + [-5\cdot (x-2)] }{(x-2)^2} =\cfrac{7x -5\cdot (x-2) }{(x-2)^2} = \\[4ex] = \cfrac{7x -5x+10 }{(x-2)^2} = \cfrac{ \bm{2x+10}}{\bm{(x-2)^2 } } \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-541ca3698314f502dae6b4144ff2180e_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{array}{l} x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}=\cfrac{x}{1} +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}= \\[4ex] =x +\cfrac{-3x}{(x-2)(x+2)} - \cfrac{2x^3-1}{2(x+1)(x+2)}= \\[4ex] = \cfrac{x\cdot 2(x-2)(x+2)(x+1)}{1\cdot 2(x-2)(x+2)(x+1)} \ + \ \cfrac{-3x\cdot 2(x+1)}{(x-2)(x+2)\cdot 2(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x+1)(x+2)\cdot (x+1)}= \\[4ex] = \cfrac{ 2x(x-2)(x+2)(x+1)}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x(x+1)}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x-2)(x+2)(x+1)}= \\[4ex]= \cfrac{ 2x^4+2x^3-8x^2-8x}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x^2-6x}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{2x^4-4x^3-x+2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - (2x^4-4x^3-x+2)}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - 2x^4+4x^3+x-2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ \bm{6x^3-14x^2-13x-2}}{\bm{2(x-2)(x+2)(x+1)}}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eba4fb225a87d253ea56ae18460f89a3_l3.png)
演習 4
次の代数分数の乗算と除算を解きます。
![]()
![]()
![]()
![]()
代数的な分数を乗算するには、まずすべての多項式を因数分解し、次に分子と分母を掛け合わせて、最後に結果の分数を単純化する必要があります。
![Rendered by QuickLaTeX.com \text{A)} \ \begin{array}{l} \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1} = \cfrac{(x+1)(x+4)}{7}\cdot \cfrac{x-1}{(x-1)(x+1)}\\[4ex] =\cfrac{(x+1)(x+4)\cdot (x-1)}{7 \cdot (x-1)(x+1)}=\cfrac{(x+1)(x+4) (x-1)}{7(x-1)(x+1)} = \\[4ex] = \cfrac{\cancel{(x+1)}(x+4)\cancel{ (x-1)}}{7\cancel{(x-1)}\cancel{(x+1)}} = \cfrac{\bm{x+4}}{\bm{7}}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc9600c8e95d957e9004296306ea25fc_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{array}{l}\cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3} = \cfrac{3(x+2)(x+3)}{3x}\cdot \cfrac{(x-1)(x+2)}{(x-1)(x+1)(x+3)}= \\[4ex] =\cfrac{3(x+2)(x+3)\cdot (x-1)(x+2)}{3x\cdot (x-1)(x+1)(x+3)}=\cfrac{3(x+2)(x+3) (x-1)(x+2)}{3x (x-1)(x+1)(x+3)} = \\[4ex] = \cfrac{\cancel{3}(x+2)\cancel{(x+3)} \cancel{(x-1)}(x+2)}{\cancel{3}x \cancel{(x-1)}(x+1)\cancel{(x+3)}} = \cfrac{(x+2)(x+2)}{x (x+1)} = \\[4ex] = \cfrac{\bm{(x+2)^2}}{\bm{x (x+1)}}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-71554d3bb6d51cfd8c3202606ca1e6e9_l3.png)
一方、代数分数を除算するには、まずすべての多項式を因数分解し、次に分数を横方向に乗算し (最初の分子と 2 番目の分母、最初の分母と 2 番目の分子)、最後に求められた代数分数を単純化します。
![Rendered by QuickLaTeX.com \text{C)} \ \begin{array}{l} \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}= \cfrac{3x}{(x+5)^2}:\cfrac{2x}{(x-5)(x+5)}=\\[4ex] = \cfrac{3x\cdot (x-5)(x+5)}{(x+5)^2\cdot 2x}=\cfrac{3x(x-5)(x+5)}{2x(x+5)^2 }= \\[4ex] =\cfrac{3\cancel{x}(x-5)\cancel{(x+5)}}{2\cancel{x}(x+5)^\cancel{2}} = \cfrac{\bm{3(x-5)}}{\bm{2(x+5)}}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8994adaa1df1f24822c8102c0d1e69c1_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{array}{l} \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2} = \cfrac{(x+3)(x+5)}{4x}:\cfrac{(x-1)(x+5)}{2x^2}= \\[4ex] = \cfrac{(x+3)(x+5)\cdot 2x^2 }{4x \cdot (x-1)(x+5)} = \cfrac{2x^2 (x+3)(x+5)}{4x (x-1)(x+5)} = \\[4ex] = \cfrac{2x^{\cancel{2}}(x+3)\cancel{ (x+5)}}{4\cancel{x} (x-1)\cancel{ (x+5)}} =\cfrac{2x(x+3)}{4(x-1)} = \cfrac{\bm{x(x+3)}}{\bm{2(x-1)}}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-961a9787bca20a2482c010586614793d_l3.png)
その説明についてどう思いますか?気に入りましたか?それとも何か提案はありますか? 💬 このページについてのご意見をコメント欄でお聞かせください。皆さんも読んでいますよ! 👀 ご質問もすべてお寄せいただけることを忘れないでください。 ❔👇❔👇