このページでは、あらゆる種類の多項式を因数分解する方法を説明します。最初にルフィニの規則を使用して多項式を因数分解する方法を見ていき、次に独立項のない多項式がどのように因数分解されるかに進み、次に分数を使用したルート多項式の因数分解を分析し、最後に因数分解の特殊なケースを分析します (注目すべき点)。恒等式、グループ化による因数分解、三項式など)。すべての説明は例で行われており、さらに最後には多項式を因数分解するための演習を段階的に解くことができます。
多項式因数分解とは何ですか?
多項式因数分解は、多項式を因数の積に分解するために数学で使用される手法です。
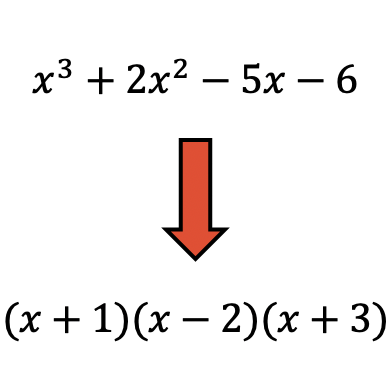
因数分解多項式を使用すると演算の実行が簡単になるため、多項式の因数分解は非常に便利です。
多項式因数分解が何であるかがわかったので、多項式がどのように因数分解されるかを見てみましょう。
ルッフィーニの法則を使って多項式を因数分解する方法
明らかに、ルフィニの規則を使用して多項式を因数分解する方法を理解するには、まずルフィニの規則を適用する方法を知る必要があります。そのため、最初に手順がどのようなものかを確認したい場合に備えて、このリンクを残しておきます。
多項式を因数分解するには、次の手順に従う必要があります。
- 多項式の根はルフィニの法則に従って計算されます。
- x=a 型で見つかった各根は、因子 (xa) の形式で表されます。
- 因数分解された多項式は、重み付けされていない多項式の最高次項の係数を乗じた、見つかったすべての因数の積です。
これがどのように行われるかを確認し、多項式の因数分解手順をよりよく理解できるように、以下に具体的な例を段階的に説明します。
- 次の多項式を因数分解します。
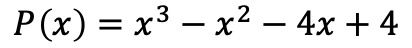
最初に行うことは、多項式の根またはゼロを計算することです。これを行うには、多項式の独立項の約数を見つける必要があります。この場合、±1、±2、±4 です。
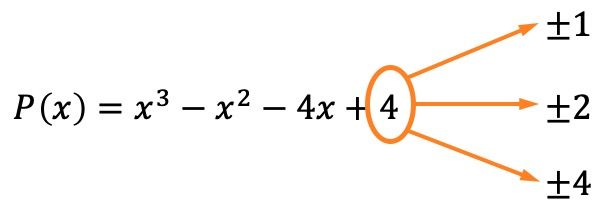
剰余と因数定理のおかげで、これらの値のいずれかによる多項式の除算の余りが 0 に等しい場合、これは、その値が多項式の根であることを意味することがわかりました。
したがって、ルフィニの法則を使用して多項式を独立項の各約数で除算し、どの場合に剰余がゼロになるかを確認する必要があります。
たとえば、次のようなルッフィーニのルールを適用することから始めます。
![]()
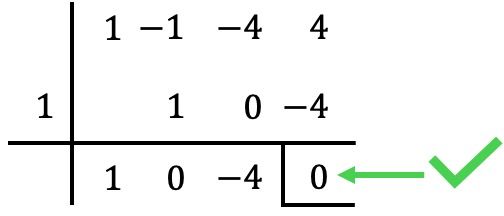
この場合、割り算の余り(または剰余)はゼロになるので、
![]()
多項式の根です。 ✅
完璧です。多項式の根はすでにあります。残っているのは、残りの根を決定することだけです。これを行うには、独立項の別の約数を含むルフィニの規則を使用します。たとえば、
![]()
また、整数多項式でルフィニの方法を使用する必要はありませんが、前のステップで中断したところから続行できます。
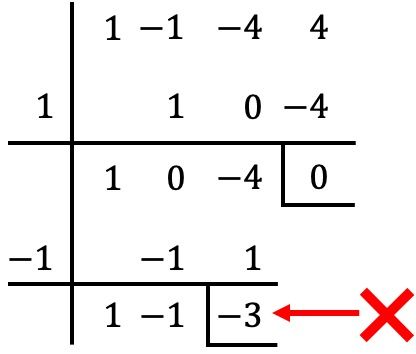
ただし、この場合、で割ると、
![]()
得られる剰余は 0 とは異なるため、
![]()
多項式の根ではありません。 ❌
したがって、別の値を試す必要があります。たとえば、Ruffini ルールを次のように実行します。
![]()
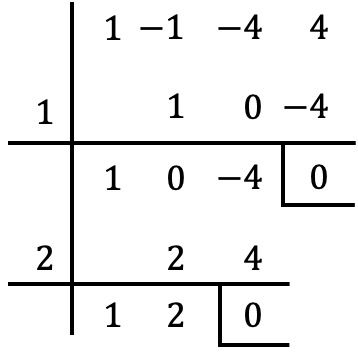
この場合もまたゼロの剰余が得られるので、
![]()
多項式の根でもあります。
そして、同じ手順を適用し続けます。次に、次のことを確認します。
![]()
それは多項式の根であるかどうか:
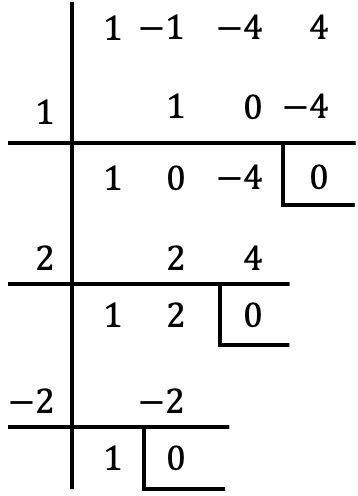
で割ると
![]()
ルッフィーニの法則を使用すると、剰余がゼロになりますので、
![]()
多項式の根またはゼロです。
したがって、ルフィニの法則を適用し続けることはできません。したがって、次の多項式の根はすべて見つかっています。
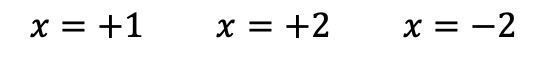
多項式の根をすべて決定したら、それを因数分解できます。これを行うには、単純に各ルートを表現します。
![]()
型の因子の形式で
![]()
つまり、ルートごとに括弧を付ける必要があります。
![]()
そしてルートの符号が変わりました:

すべての根を因数として表現したので、すべての括弧に元の多項式の最高次項の係数を乗算する必要があります。
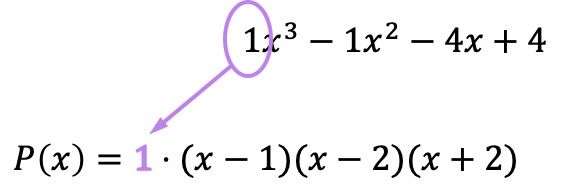
この場合、係数は 1 なので結果には影響しませんが、この乗算を忘れずに実行することが重要です。この係数が 1 と異なる場合、因数分解された多項式が変化するため、数値を入力しないと多項式の因数分解でエラーが発生します。
つまり、因数分解された多項式は次のようになります。
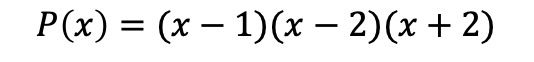
独立項のない多項式の因数分解
独立項は、多項式の考えられる根を特定できるため、多項式の因数分解にとって重要であることがわかりました。しかし、独立項のない多項式をどのように因数分解するのでしょうか?
独立項のない多項式を因数分解するには、まず多項式の共通因数を抽出し、次にルフィニの法則を使用して共通因数を含まない多項式の根を抽出する必要があります。
このように書くと、少し複雑に聞こえるかもしれません。それでは、共通因数を使用して多項式を因数分解する方法を確認できるように、例を段階的に解決してみましょう。
- 次の多項式の階乗分解を実行します。
![]()
ご覧のとおり、問題の多項式には独立した項がないため、多項式の共通因数を取る必要があります。よく見ると、多項式のすべての要素には少なくとも 1 つの要素があります。
![]()
したがって、共通因数は
![]()
したがって、多項式から共通因数を抽出すると、次の式が得られます。
![]()
そして、多項式の共通因数を抽出したら、ルフィニの規則を適用して、括弧内にグループ化された多項式の根を計算します (前のセクションで説明した手順を使用)。
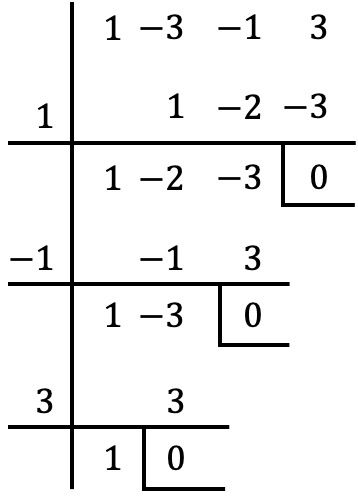
したがって、括弧内の多項式の根またはゼロは次のようになります。
![]()
したがって、多項式を因数分解するには、(上のセクションで説明したように) かっこ内の多項式を因数形式の根に置き換えるだけです。
![Rendered by QuickLaTeX.com \begin{array}{c}P(x) = x\left(x^3-3x^2-x+3\right) \\[2ex]\color{red} \bm{\downarrow} \\[2ex] \bm{P(x) = x(x-1)(x+1)(x-3)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-470b8a931d73b852bee700a6488af525_l3.png)
このようにして、次数 0 の項を持たない多項式をすでに因数分解しました。唯一の違いは、最初に共通因数を抽出する必要があることですが、以降の手順はすべてまったく同じであることに注意してください。
一方で、知っておくべきことは、
![]()
共通因数を抽出すると、多項式の根の 1 つが次のことを意味するため、これは多項式の根でもあります。
![]()
したがって、多項式の根はすべて次のようになります。
![]()
実際、多項式には次数が示すのと同じ数の根がなければなりません。この場合、多項式の次数は 4 であるため、根は 4 つあります。
有理根による多項式の因数分解
これまで、整数根を持つ多項式の因数分解の例を見てきましたが、多項式は有理根、つまり分数を持つこともできます。このタイプの多項式因数分解がどのように解決されるかを例で見てみましょう。
- 次の不完全多項式を因数分解します。
![]()
いつものように、独立項の約数を含むルフィニの規則を使用して、多項式の根を決定しようとします。
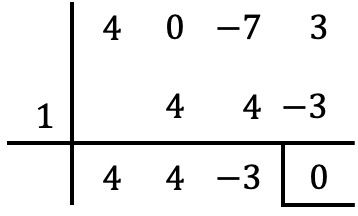
しかし、独立項の他のすべての約数を使ってルフィニを計算しようとすると、ゼロ以外の剰余が得られるため、ルフィニを使用してこれ以上の根を計算することはできません。
したがって、私たちは、次のような状況に陥っています。
![]()
除算の余りは 0 に相当します。これは、多項式が分数根を持つことができることを意味します。これらの根を求めるために、分数を使用してルフィニを適用することもできますが、計算で間違いを犯しやすいため、このような場合は通常次のことを行います。
整数根を使用してルフィニの規則を適用し続けることができない場合は、最後に得られた多項式を 0 に設定し、結果の方程式を解く必要があります。したがって、多項式の根は方程式から求められた値になります。
一方、方程式に解がない場合は、多項式に根がなくなり、完全に因数分解できないことを意味します。
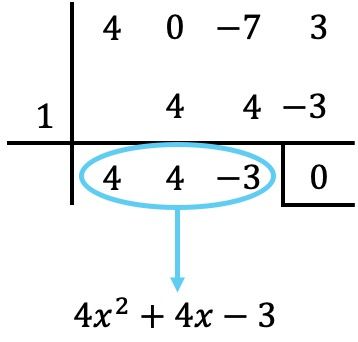
したがって、商多項式をゼロに設定します。
![]()
そして、二次方程式の公式を使用して、結果の方程式を解きます。
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{-4 \pm 8}{8} = \begin{cases} \cfrac{-4+8}{8} = \cfrac{4}{8} = \cfrac{1}{2} \\[4ex]\cfrac{-4-8}{8} = \cfrac{-12}{8} = -\cfrac{3}{2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f52601e0daafdb92974cfbfe6613733b_l3.png)
したがって、多項式の根は次のようになります。
![]()
したがって、多項式には分数の形式の根があります。
多項式の根がすべて分かれば、各根を表現することで因数分解された多項式を簡単に見つけることができます。
![]()
型の因子の形式で
![]()
つまり、ルートごとに括弧を付ける必要があります。
![]()
そしてルートの符号が変わりました。
![]()
多項式を因数分解するには、その因数に因数分解されていない多項式の最高次項の係数 (この場合は 4) を乗算する必要があることに注意してください。
因数分解多項式の特殊なケース
通常、上で説明したように、ルフィニの法則 (または合成除算) を使用して多項式を因数分解します。ただし、問題の多項式によっては、多項式因数分解をより速く実行できる場合があります。以下では、これらの特定のケースをそれぞれ見ていきます。
著名な人物の因数分解
多項式が注目すべき恒等式 (または注目すべき積) に対応していることがわかれば、それを因数分解するのは非常に簡単です。ただし、これを行うには、 著名なアイデンティティの公式をマスターする必要があります。そうでない場合は、公式を見つけるだけでなく、著名な人物の例も確認できるこのリンクを参照することをお勧めします。アイデンティティを段階的に解決し、演習を行うこともできます。
平方の差
よく知られているように、二乗の差の注目すべき恒等式は次のとおりです。
![]()
したがって、次の式を満たす多項式が見つかった場合、
![]()
直接考慮することができます。
二乗の差が考慮される次の例を見てください。
![]()
一方、多項式の根は次のとおりです。
![]()
二乗の差である二項因数分解の他の例:
![]()
![]()
![]()
足し算と引き算の二乗
残り 2 つの主要な恒等式、加算平方と減算平方の公式はすでに知っているはずです。
サムスクエア
![]()
減算二乗
![]()
したがって、多項式がこれら 2 つの注目すべき恒等式のいずれかに対応していることがわかれば、それを直接因数分解することができます。次の例を見てください。
![]()
デュアルルート:
![]()
![]()
デュアルルート:
![]()
これらの注目すべき製品タイプを特定するのは少し難しくなります。秘訣は、多項式の独立項がある数の 2 乗であるかどうか、および高次の項が単項式の 2 乗であるかどうかを確認することです (通常は
![]()
)、この場合、それが真実であることを確認するだけで十分です。
![]()
中間ディプロマの終了と同じです。
たとえば、次の多項式があるとします。
![]()
この場合、多項式のすべての要素が正であるため、和の 2 乗のみが可能です。したがって、変数
![]()
式の は、独立項の根であり、変数であるため、5 でなければなりません。
![]()
それは違いない
![]()
、これは「maydegree」という用語の語源であるためです。
![]()
![]()
ここで私たちがしなければならないのは、和の二乗の公式が中次項で満たされることを証明することだけです。
![]()
![]()
✅
注目すべき積の公式が満たされるため、因数分解された多項式は次のようになります。
![]()
そして、この多項式の根は、
![]()
これは、係数が 2 乗される (2 回繰り返される) ため、二重根になります。
以下に、完全二乗三項式の因数分解のその他の例を示します。
![]()
![]()
![]()
2次三項式の因数分解
これまで見てきたように、完全な平方である三項式が存在する場合があり、これらは注目すべき恒等式の公式で直接因数分解することができます。しかし、ほとんどの三項式は注目すべき積ではありません。では、これらの多項式の場合をどのように因数分解するのでしょうか?
二次多項式を因数分解するには、ルフィニ法を適用する必要はありません。多項式をゼロに設定し、結果として得られる二次方程式を解くだけです。したがって、方程式の解は多項式の根になります。
たとえば、次の 2 次多項式を因数分解するように求められたとします。
![]()
Ruffini を使用する代わりに、多項式を 0 に設定します。
![]()
次に、2 次方程式の公式を使用して、方程式の解を求めます。
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{-2 \pm 8}{2} = \begin{cases} \cfrac{-2+8}{2} = \cfrac{6}{2} = 3 \\[4ex]\cfrac{-2-8}{2} = \cfrac{-10}{2} = -5 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cd949c11577e283ded1f45e1ba2fa35b_l3.png)
したがって、多項式の根は次のようになります。
![]()
そして最後に、多項式因数分解は次のようになります。
![]()
偶数の指数を使用した 4 次三項式の因数分解
前のケースと同様に、偶数の指数を持つ 4 次多項式を因数分解するには、多項式をゼロに設定し、二乗方程式を解く必要があります。見つかった値が多項式の根に対応するようにします。
例として、次の 4 次の多項式を因数分解します。
![]()
まず、多項式をゼロに設定します。
![]()
次に、二乗方程式を解く必要があります。これを行うには、変数を変更します。
![]()
![]()
次の式を使用して二次方程式を解きます。
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle t = \cfrac{5 \pm 3}{2} = \begin{cases} \cfrac{5+3}{2} = \cfrac{8}{2} = 4 \\[4ex]\cfrac{5-3}{2} = \cfrac{2}{2} = 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d5dada92a4b578d23d0e32ab6dac388_l3.png)
変数の変更をキャンセルして根を計算します。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
したがって、多項式の根は次のようになります。
![]()
そして、多項式の根またはゼロがわかったら、その根を因数の形式で代数的に表すことによって因数分解します。
![]()
グループ化による多項式の因数分解
非常に特殊な場合には、式を使用して、非常に特殊なタイプの多項式を因数分解することができます。
次の形式の多項式があるとします。
![]()
共通因数を削除することで多項式を単純化できます。
![]()
そして、共通因数を 2 回抽出することで、多項式をさらに単純化できます。
![]()
このようにして、ルフィニや他の方法を適用せずに多項式を因数分解することができました。そして、上記の多項式の根は次のようになります。
![]()
次に、この方法を数値例で見てみましょう。
![]()
まず、次の共通因数を削除します。
![]()
そして2の場合:
![]()
そして今のように
![]()
が多項式の共通因数である場合、次の共通因数を抽出します。
![]()
![]()
したがって、多項式の根は次のようになります。
![]()
この方法は、二重公約数抽出による多項式の因数分解とも呼ばれます。これは非常に迅速な手順ですが、この方法で因数分解するとエラーが頻繁に報告されるため、このタイプの因数分解を実行することはお勧めしません。さらに、上で見たように、単純な二次方程式を解くことによって、次数 2 の多項式を因数分解することもできます。つまり、この方法をよく理解していないと何も始まりません。
最後に、LLL アルゴリズム、クロネッカー法、トラガー法など、さらに複雑な多項式因数分解法が他にもあることに注意してください。これらは数学的に難しいため、ここでは説明しません。
因数分解多項式に関する演習を解決しました
すべての種類の因数分解多項式を確認したら、演習を解いて練習することをお勧めします。このため、以下に多項式を因数分解するための段階的な解決演習をいくつか用意しました。ご質問がございましたら、コメントに書き込んでいただければすぐにお答えいたします。
演習 1
次の 3 次多項式の因数分解を実行します。
![]()
これは、完全で順序付けられた 3 次の、最終的には独立した多項式です。したがって、ルフィニの方法を適用して多項式の根を決定します。
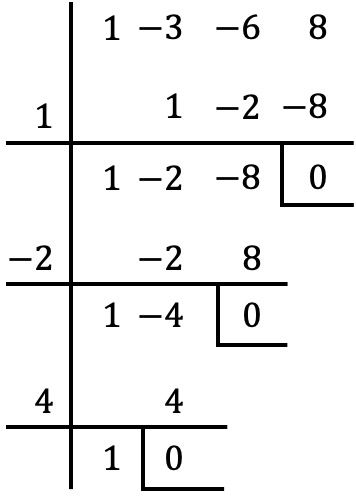
したがって、多項式の根は次のようになります。
![]()
したがって、多項式因数分解は次のようになります。
![]()
![]()
演習 2
次の 4 次多項式の因数分解を計算します。
![]()
これは 4 次の多項式であり、独立した項があるため、ルフィニ法を使用して多項式の根を求めます。
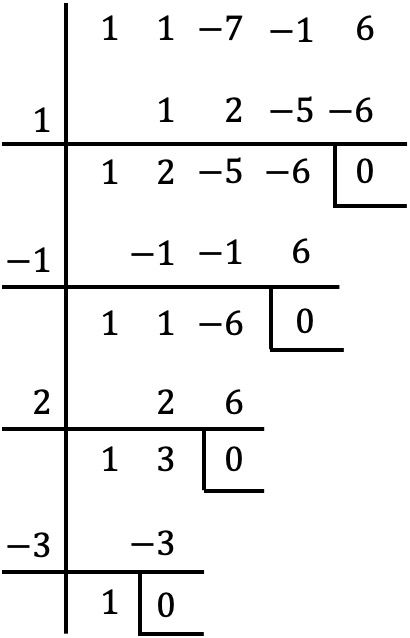
したがって、多項式の根は次のようになります。
![]()
そして、多項式を因数分解すると、次のようになります。
![]()
![]()
演習 3
次の 4 次多項式の因数分解を求めます。
![]()
この場合、多項式には独立項がないため、最初に共通因数を抽出する必要があります。
![]()
x の共通因数を取得したので、ルフィニの方法を使用してかっこ内の多項式の根またはゼロを計算します。
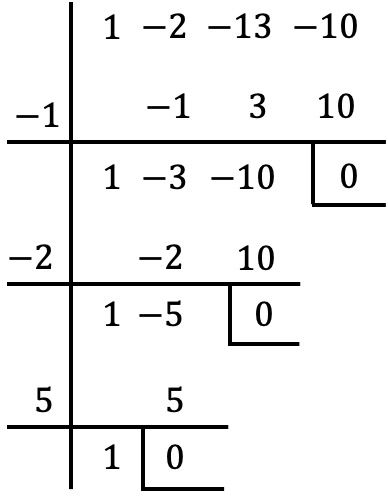
したがって、多項式の根は、ルフィニ法で求めた根に共通因数の x=0 を加えたものになります。
![]()
最後に、多項式を因数に分解すると、次の式が得られます。
![]()
![]()
演習 4
次の 3 次多項式を因数に変換します。
![]()
この多項式には独立した項があるため、Ruffini アルゴリズムを使用してその根を計算します。
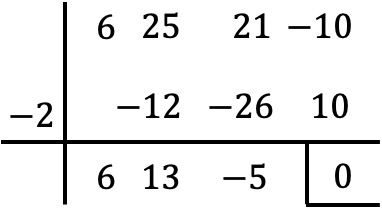
ただし、この点に達すると、別の整数がないと割り算の余りがゼロになるため、ルフィニの法則を適用し続けることはできません。
したがって、結果の多項式をゼロに設定します。
![]()
そして、二次方程式の公式を適用して、結果の方程式を解きます。
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{-13 \pm 17}{12} = \begin{cases} \cfrac{-13+17}{12} = \cfrac{4}{12} = \cfrac{1}{3} \\[4ex]\cfrac{-13-17}{12} = \cfrac{-30}{12} = -\cfrac{5}{2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-77785f81018b1d7a46a83d1567af638e_l3.png)
したがって、多項式の根またはゼロは次のようになります。
![]()
したがって、多項式の因数分解は分数を使用して行う必要があります。
![]()
演習 5
次の 6 次多項式の因数分解を求めます。
![]()
問題の多項式には独立した項がないため、最初に共通因数を抽出する必要があります。この場合、共通因数は次のようになります。
![]()
![]()
そして、多項式から共通因数を削除したら、ルフィニの法則を使用してかっこ内の多項式の根を求めます。
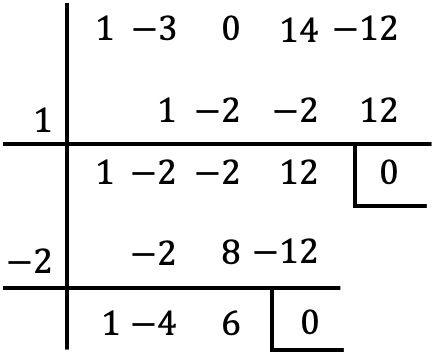
しかし、この段階に到達すると、別の整数がないと余りがゼロになるため、先に進むことはできません。
したがって、得られた多項式をゼロに設定します。
![]()
そして、二次方程式を次の式で解きます。
![]()
![]()
負の数には根がないため、方程式には解がありません。これは、多項式の根をこれ以上見つけることができないことを意味します。言い換えれば、多項式は完全には因数分解可能ではありません。
ただし、私たちが見つけることができたルーツは次のとおりです。
![]()
ルートに注意してください
![]()
から共通因数を削除したため、 は 2 回繰り返されます。
![]()
そしてそれは二乗なので、これは二重根であることを意味します。
結論として、因数分解された多項式は、因数として表現されたすべての根の積になります。
![]()
ルッフィーニの法則から得られた多項式を乗算しますが、これ以上考慮することはできません。
![]()
![]()
演習 6
次のすべての多項式の因数分解を実行します。
![]()
![]()
![]()
![]()
セクション A) の多項式は、注目すべき単位、特に和の二乗に対応します。したがって、その因数分解は次のようになります。
![]()
セクション B) の多項式も注目すべき積であり、特に二乗の差であるため、次のようになります。
![]()
同様に、セクション C) の多項式は注目に値する等式であり、特に減算の 2 乗で構成されます。したがって、その因数分解は次のようになります。
![]()
最後に、パート D) の多項式は注目すべき恒等式ではありません。したがって、多項式を 0 に設定し、結果の方程式を解いてその根を見つける必要があります。
![]()
二次方程式の公式を使用します。
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{-10 \pm 2}{2} = \begin{cases} \cfrac{-10+2}{2} = \cfrac{-8}{2} = -4 \\[4ex]\cfrac{-10-2}{2} = \cfrac{-12}{2} = -6\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-88934cfbe80af987a03e4fb1a2a72aa7_l3.png)
したがって、多項式 D) の根は次のようになります。
![]()
そして最後に、多項式因数分解の結果は次のようになります。
![]()