▷ 剰余定理: その概要、例、および演習問題 ✅

ここでは、剰余定理 (または剰余定理) とは何か、およびそれが多項式にどのように適用されるかについて説明します。また、例を見て、さらに、剰余定理に関するステップバイステップの解決済み演習で練習することもできます。

剰余定理とは何ですか?

数学における剰余定理は、任意の多項式 P(x) を (xa) の形式の別の多項式で除算した余りは、値 x=a の場合の多項式 P(x) の数値に等しいことを示します。言い換えれば、除算の余り P(x):(xa) は P(a) と等価です。

剰余定理の例

剰余定理とは何かを理解したら、その応用例を見てみましょう。

次の 2 つの多項式間の除算の余りを計算します。

$P(x) = x^3+2x^2-4x+3 \qquad \qquad Q(x)=x-1$

$\cfrac{P(x)}{Q(x)}$

多項式の除算の余り (または剰余) を求めるには、剰余定理を利用できます。この場合、除算多項式は (xa) の形式、つまり 1 次の係数であるためです。変数 x は 1 であり、独立した項を持ちます。

そこで、このような除算の余りは、符号を変えた除数多項式の独立項で評価される被除数多項式の数値、つまり P (1) に等しいという剰余定理を適用します。

したがって、除算の余りを求めるには、x=1 で多項式を評価する必要があります。

$\begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}$

したがって、多項式間の除算の余りは 2 になります。

一方、 多項式の除算に関するルフィニの規則を使用して、剰余が見つかった結果と一致するかどうかを確認することもできます。

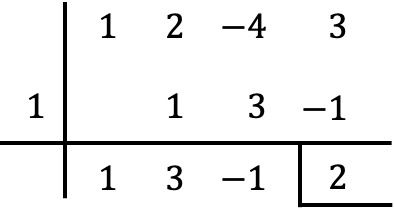
ご覧のとおり、剰余定理を使用して二項式で多項式を除算した余りを求める方が、ルフィニの規則を使用するよりもはるかに高速かつ簡単です。これは、実行される計算がはるかに少ないためです。

剰余と因数定理

剰余定理と多項式の根 (またはゼロ) の定義から、因数定理を推定できます。したがって、因数定理は次のことを意味します。

因数定理では、P(a)=0 の場合に限り、多項式 P(x) は形式 (xa) の別の多項式で割り切れます。そしてこの場合、それは a が多項式 P(x) の根またはゼロであることを意味します。

さらに、剰余定理によれば、これは、多項式が別の多項式で割り切れる場合、P(a)=0 であるため、前記割り算の余りはゼロになることを意味します。

たとえば、特定の多項式があるとします。

$P(x)=x^2+2x-8$

P(2)=0 であるため、この多項式は二項 (x-2) で割り切れます。

$\begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}$

x=2 は多項式 P(x) をキャンセルするため、これは x=2 が前記多項式の根であることを意味します。

さらに、P(2)=0 であるため、剰余定理のおかげで、割り算の剰余が次のようにわかります。

$\cfrac{x^2+2x-8}{x-2}$

は0に等しい。

剰余定理の演習を解いた

剰余定理の理解を完了するために、練習できるように段階的に解決されるいくつかの演習を用意しました。まずは自分でこの演習を試してから、正しく実行できたかどうかを確認することをお勧めします。

演習 1

剰余定理により、多項式の除算の剰余を求めます。

$\cfrac{P(x)}{Q(x)}$

、演算に関係する多項式です。

$P(x) =x^3+4x^2-2x+1\qquad \qquad Q(x)=x-2$

解決策を見る

除数多項式は1次項と独立項のみで構成されており、しかも1次項の係数は1なので剰余定理が使えます。

そして、剰余定理を適用するには、符号を変えた除数多項式の独立項で被除多項式を評価するだけで十分です。つまり、P(2) を計算する必要があります。

$\begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}$

したがって、2 つの多項式間の除算の余りは 21 になります。

演習 2

多項式を考えると

$P(x)=x^4-2x^3+5x^2-3x+4 ,$

次の各多項式で割った余りを求めます。

$\text{A)} \ \left(x-1 \right)$
$\text{B)} \ \left(x+1 \right)$
$\text{C)} \ \left(x+2 \right)$
$\text{D)} \ \left(x-3 \right)$

解決策を見る

すべての除算多項式は剰余定理の条件を満たすため、この定理を使用して各除算の剰余を求めることができます。

$\begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}$

$\begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}$

$\begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}$

$\begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}$

演習 3

パラメータの価値を計算する

$m$

多項式の除算の余りが

$\cfrac{P(x)}{Q(x)}$

両方とも多項式であり、3 に等しくなります。

$P(x) =x^3-5x^2-mx+9 \qquad \qquad Q(x)=x+3$

解決策を見る

この場合、除算多項式は 1 次の単項式と独立項で構成され、さらに 1 次の単項式の係数は 1 です。したがって、剰余定理を使用できます。

剰余定理を使用するには、分割多項式の独立項を符号の変更に置き換えるだけです。分割多項式に x があるため、P(-3) を解く必要があります。

$\begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}$