この記事では、グラフ上であらゆるタイプの関数を表現する方法を見ていきます。さらに、グラフ上で関数を表現するための段階的な演習も用意されています。
グラフ上で関数を表現する方法
グラフ上で関数を表すには、次の手順を実行する必要があります。
- 関数のドメインを見つけます。
- デカルト軸を使用して関数のカットオフ点を計算します。
- 関数の漸近線を計算します。
- 関数の単調性を研究し、その相対的な極値を見つけます。
- 関数の曲率を調べて、その変曲点を見つけます。
- カットオフ点、漸近線、相対極値、変曲点をプロットしてから、関数をプロットします。
関数の表現例
関数がどのようにグラフィカルに表現されるかを確認できるように、次の演習を段階的に解決していきます。
- 次の有理関数をグラフにプロットします。
![]()
最初に行うことは、関数の定義域を計算することです。これは有理関数であるため、どの数値が関数の定義域に属していないのかを確認するには、分母をゼロに設定する必要があります。
![]()
![]()
したがって、x が 1 の場合、分母は 0 になるため、関数は存在しません。したがって、関数の定義域は、x=1 を除くすべての実数で構成されます。
![]()
X 軸との交点を見つけるには、次の方程式を解く必要があります。
![]()
関数の X 軸の値は常に 0 であるため、次のようになります。
![]()
![]()
用語
![]()
これには左側全体を除算する必要があるため、右側全体を乗算できます。
![]()
![]()
![]()
したがって、OX 軸との交点は次のようになります。
![]()
そして、 Y 軸との交点を見つけるために、次のように計算します。
![]()
Y 軸上の x は常に 0 であるため、次のようになります。
![]()
したがって、OY 軸のカットオフ ポイントは次のようになります。
![]()
この場合、関数が座標原点を通過すると、X軸との交点とY軸との交点が一致する。
定義域とカットオフ点がわかったら、関数の漸近線を計算する必要があります。
関数に垂直方向の漸近線があるかどうかを確認するには、領域に属さない点 (この場合は x=1) での関数の極限を計算する必要があります。結果が無限であれば、それは垂直方向の漸近線です。まだ:
![]()
x が 1 になる傾向があるときの関数の極限は無限大を与えるため、x=1 は垂直漸近線になります。
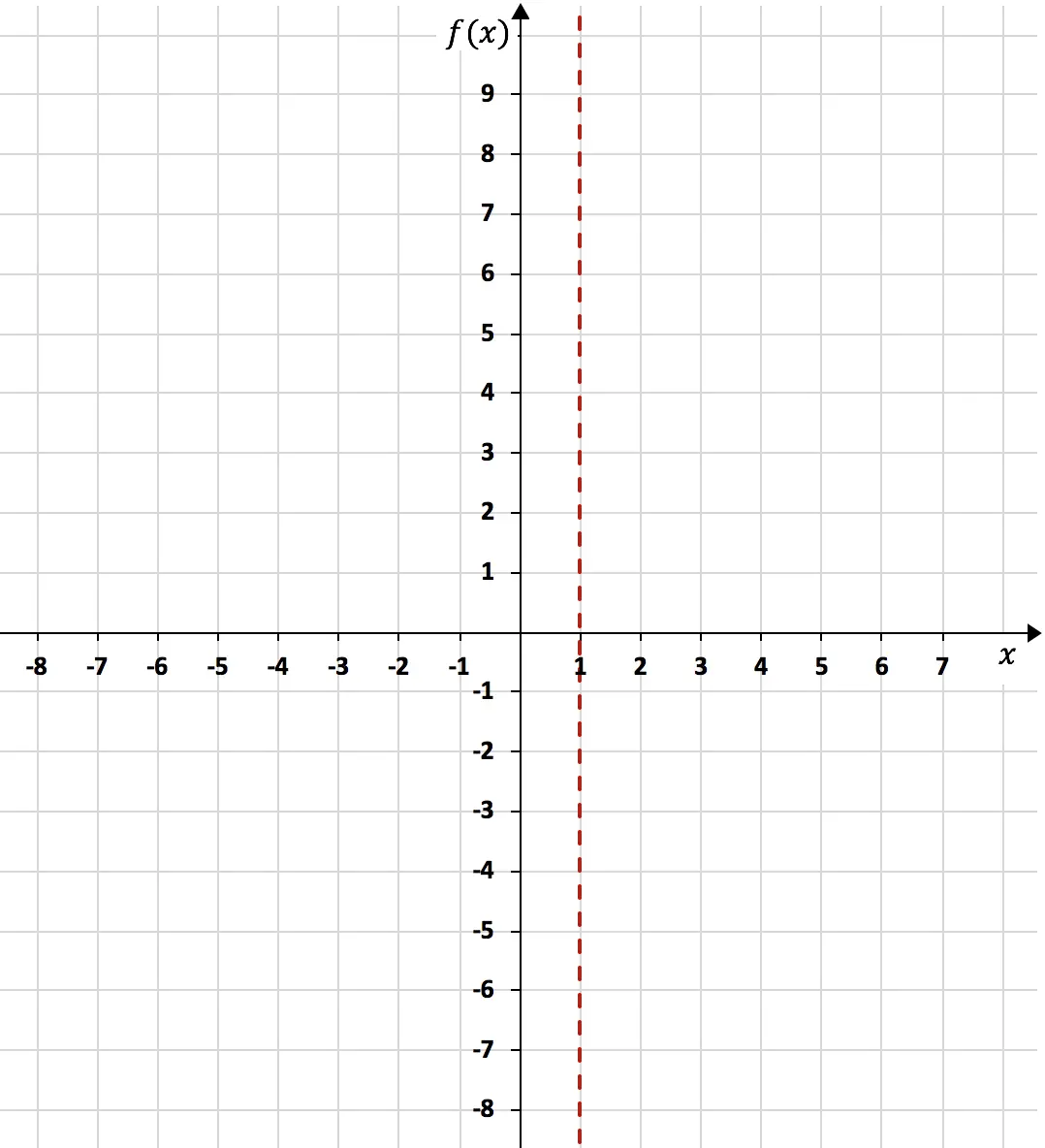
垂直漸近線を計算したら、それに対する関数の横方向の限界を計算する必要があります。関数が左から x=1 に近づくときに -∞ になる傾向があるのか、+∞ になる傾向があるのかがわかりません。また、右から x=1 にいつ近づくのかもわかりません。
したがって、x=1 における関数の左横限界の計算に進みます。
![]()
ある点の横方向の境界を数値的に計算するには、その点に非常に近い関数に数値を代入する必要があります。この場合、左側には 0.9 など、1 に非常に近い数値が必要です。したがって、関数内のポイント 0.9 を次のように置き換えます。
![]()
漸近線の横方向の制限では、+∞ または -∞ しか得られません。そして、左側の 1 に非常に近い数値を関数に代入すると負の結果が得られるため、左側の制限は -∞ になります。
![]()
次に、右側の境界に対して同じ手順を実行します。
![]()
右側の 1 に非常に近い数値を関数に代入します。たとえばポイント 1.1:
![]()
この場合、サイド制限の結果は正の数になります。したがって、右側の極限は +∞ です。
![]()
結論として、x=1 では、関数は左側でマイナス無限大、右側でプラス無限大に向かう傾向があります。
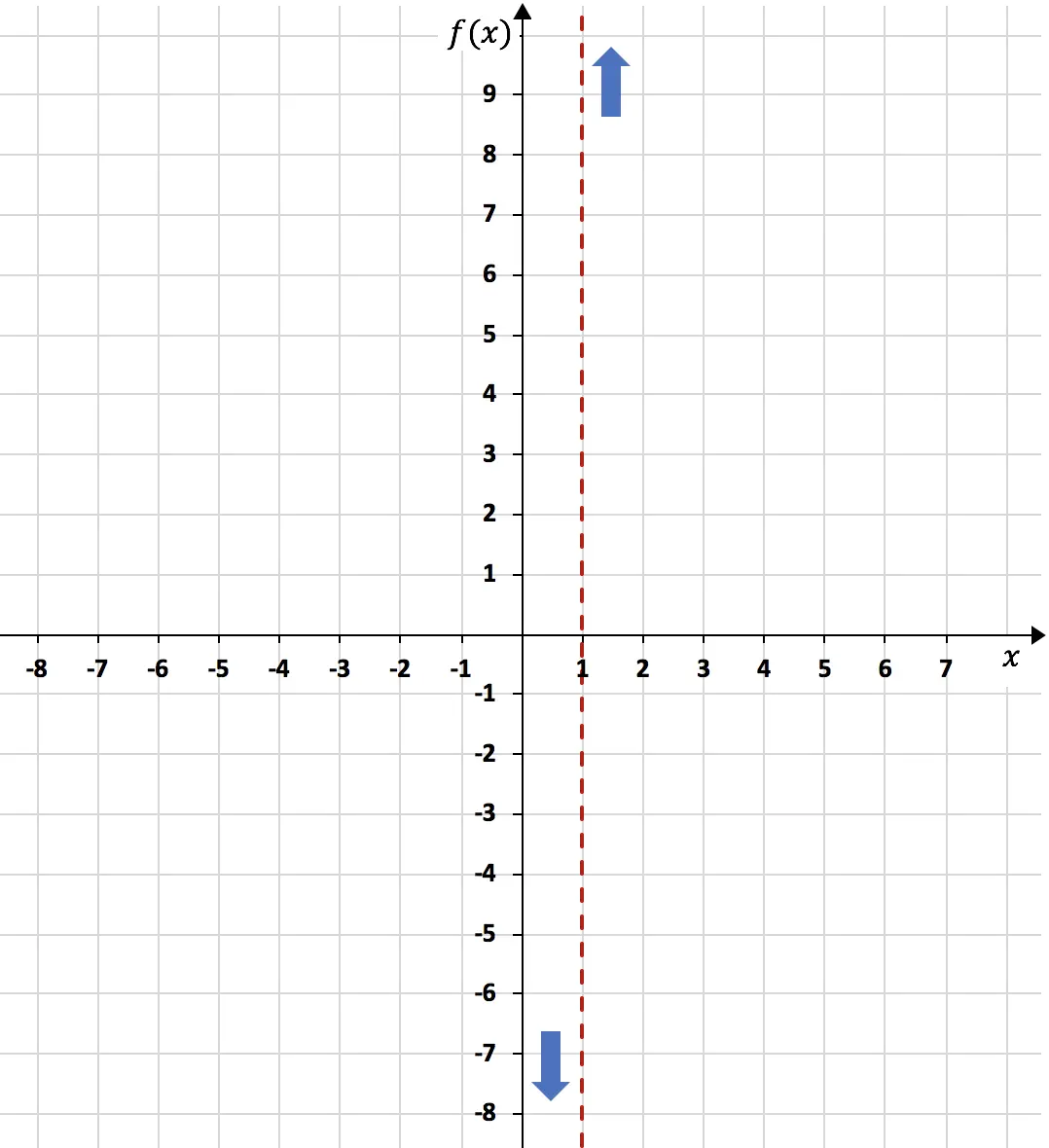
一方、関数の水平方向の漸近線は、関数の無限極限の結果になります。まだ:
![]()
有理関数の無限限界を計算する方法を思い出してください。
![\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”></p>
</p>
</div>
<p>関数の無限限界により +∞ が得られるため、この関数には水平方向の漸近線がありません。</p>
<p>次に、斜めの漸近線を計算します。斜めの漸近線は次の形式になります。</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c969e4b99985b44006e57d554ff0247_l3.png)
![]()
。そして
![]()
次の式で計算されます。
![]()
![]()
x は、分母が 1 であるかのようになります。
![]()
これは分数の割り算なので、横に掛けます。
![]()
![]()
そして、限界を計算します。
![]()
したがって、m=1となります。今計算してみましょう
![]()
次の式で:
![]()
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty](https://mathority.org/wp-content/ql-cache/quicklatex.com-10dfa8fdcfbf0c978e02374654a66b7d_l3.png)
しかし、無限大から無限大を引いた不確定性が得られるため、項を共通の分母に減らす必要があります。これを行うには、項 x を分数の分母で乗算および除算します。
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-70026c2aed1bb58a120f8c18423d9ef5_l3.png)
2 つの項の分母が同じになったので、それらをグループ化できます。
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-7702287a02af6d8e3dddaa3f0c6eb1b5_l3.png)
そして最後に、制限を解決します。
![Rendered by QuickLaTeX.com \displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-feb5faa9dc5d3b68d3273ad4d75d2bb1_l3.png)
したがって、n = 1。したがって、斜めの漸近線は次のようになります。
![]()
![]()
![]()
斜めの漸近線を計算したら、値のテーブルを作成して同じグラフ上にそれを表します。
![]()

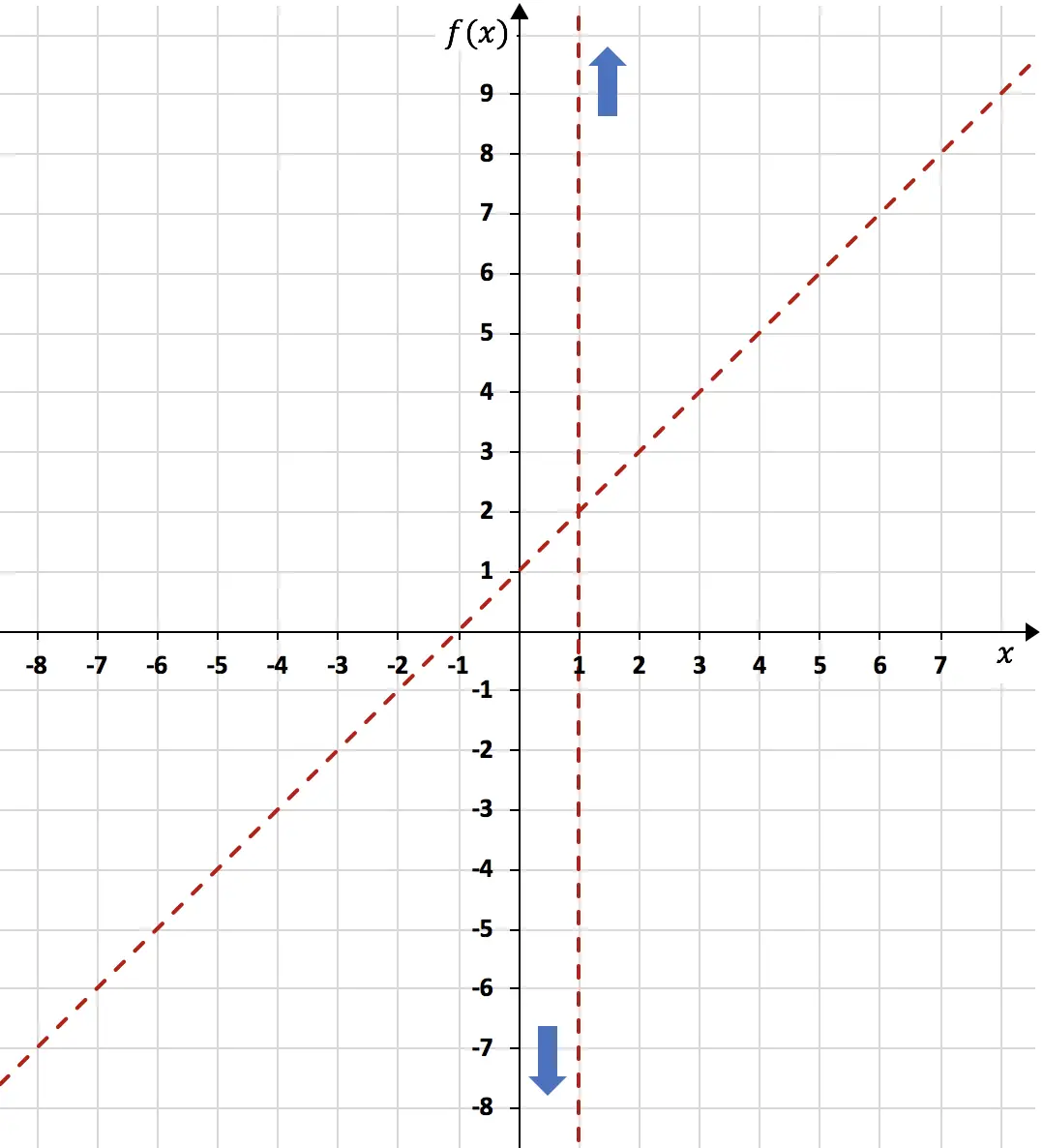
関数の漸近線がすべてわかったので、次は関数の単調性を分析する必要があります。つまり、どの区間で関数が増加し、どの区間で関数が減少するかを研究する必要があります。したがって、関数の一次導関数を計算します。
![]()
![]()
そして、微分値を 0 に設定して方程式を解きます。
![]()
![]()
用語
![]()
これには左側全体を除算する必要があるため、右側全体を乗算できます。
![]()
![]()
二次方程式を解くために共通因数を抽出します。
![]()
乗算が 0 になるには、乗算の 2 つの要素のうちの 1 つがゼロでなければなりません。したがって、各係数を 0 に設定し、方程式の両方の解を取得します。
![Rendered by QuickLaTeX.com \displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55127e675ce8f7742db17d565c2ae507_l3.png)
ここで、見つかったすべての臨界点、つまり定義域に属さない点 (x=1) と導関数をキャンセルする点 (x=0 および x=2) を数直線上に表します。

そして、関数が増加するか減少するかを知るために、各区間の導関数の符号を評価します。したがって、各区間の点 (臨界点ではない) を取得し、その点で導関数がどのような符号を持つかを調べます。
![]()
![]()
![]()
![]()
![]()
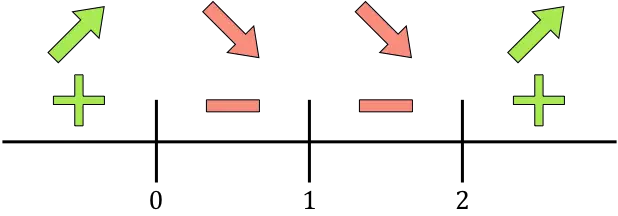
導関数が正の場合、関数が増加していることを意味し、導関数が負の場合、関数が減少していることを意味します。したがって、成長と衰退の間隔は次のようになります。
成長:
![]()
減少:
![]()
さらに、x=0 では関数は増加から減少に移行するため、x=0 は関数の相対最大値になります。そして、x=2 では、関数は減少から増加に移行するため、x=2 は関数の相対最小値となります。
最後に、見つかった極値を元の関数に代入して、点の Y 座標を求めます。
![]()
![]()
したがって、関数の相対的な極値は次のようになります。
最大オンポイント
![]()
最小点まで
![]()
最大値と最小値をグラフに表します。
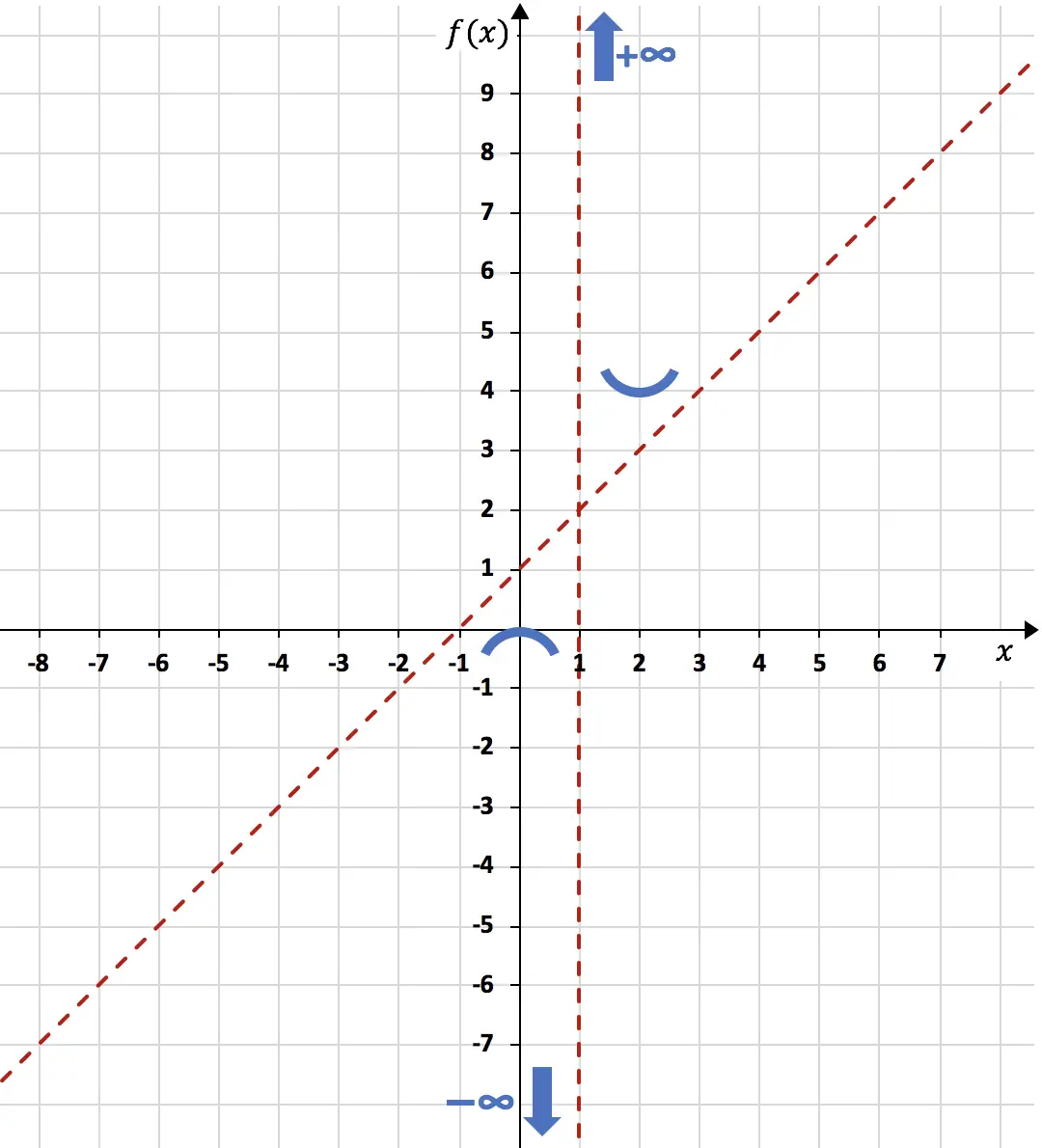
最後に、関数の曲率、つまり関数の凹凸の間隔を調べるだけで十分です。これを行うために、その二次導関数を計算します。
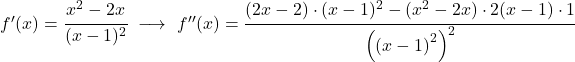
![]()
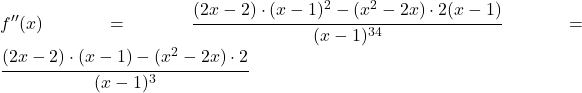
![]()
![]()
そして、二次導関数をゼロに設定して方程式を解きます。
![]()
![]()
![]()
![]()
2 が 0 に等しくなることは決してないので、次の方程式は
![]()
解決策はありません。
ここで、見つかったすべての臨界点、つまり定義域 (x=1) に属さない点と、二次導関数をキャンセルする点 (この場合、そうでない点はありません) を数直線上に表します。

そして、関数が凸であるか凹であるかを知るために、各区間の導関数の符号を評価します。したがって、各区間の点 (決して特異点ではない) を取得し、この点で導関数がどのような符号を持つかを調べます。
![]()
![]()
![]()

そして最後に関数の凹凸の間隔を導き出します。二次導関数が正の場合、関数が凸であることを意味します。
![]()
、二次導関数が負の場合、これは関数が凹であることを意味します
![]()
。したがって、凹凸の間隔は次のようになります。
凸型
![]()
:
![]()
凹面
![]()
:
![]()
ただし、x=1 で曲率の変化があっても、それは変曲点ではありません。 x=1 は関数の定義域に属さないためです。
したがって、計算したすべてを使用して関数の表現を完了できます。
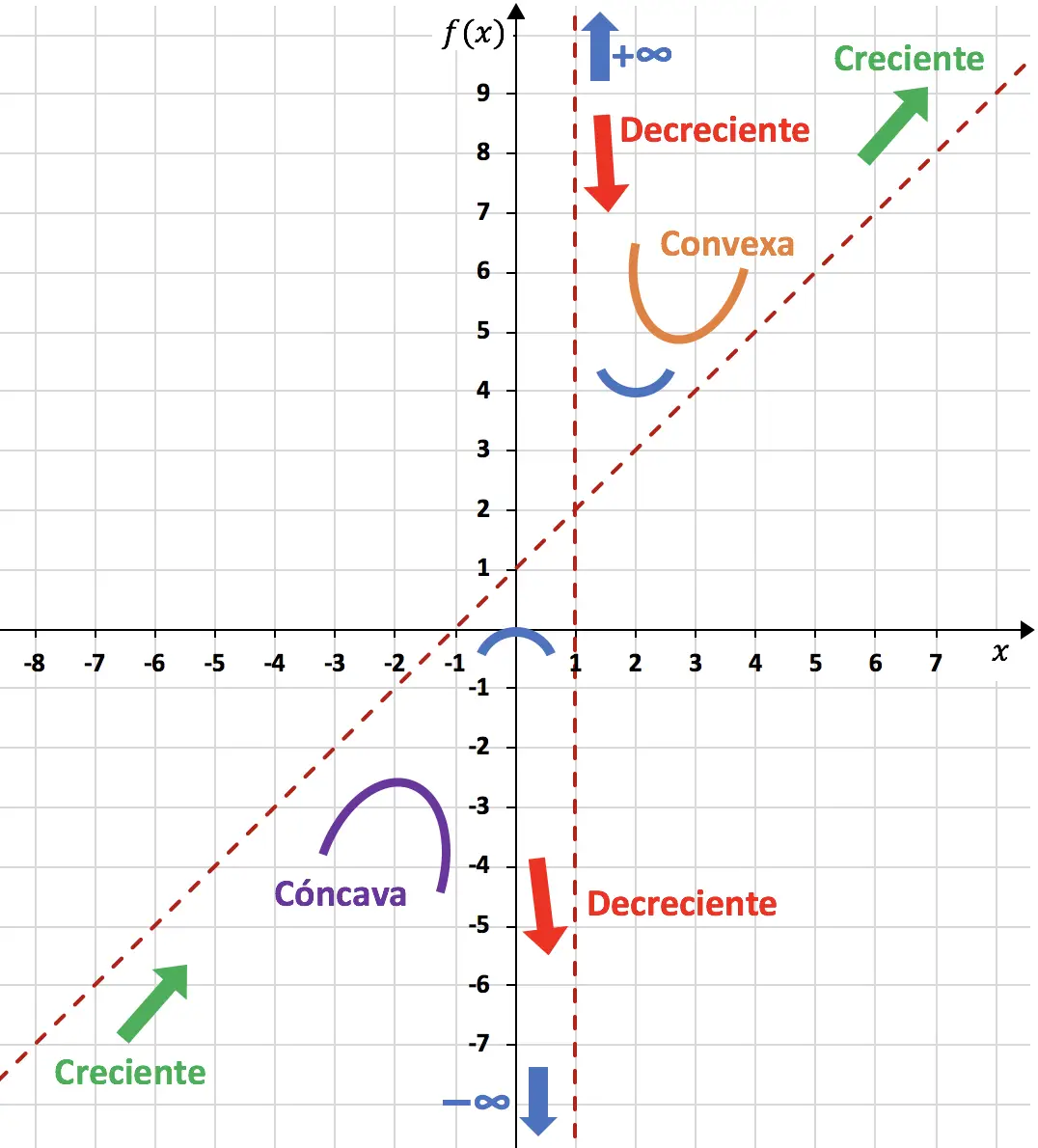
したがって、グラフ上で表される関数は次のようになります。
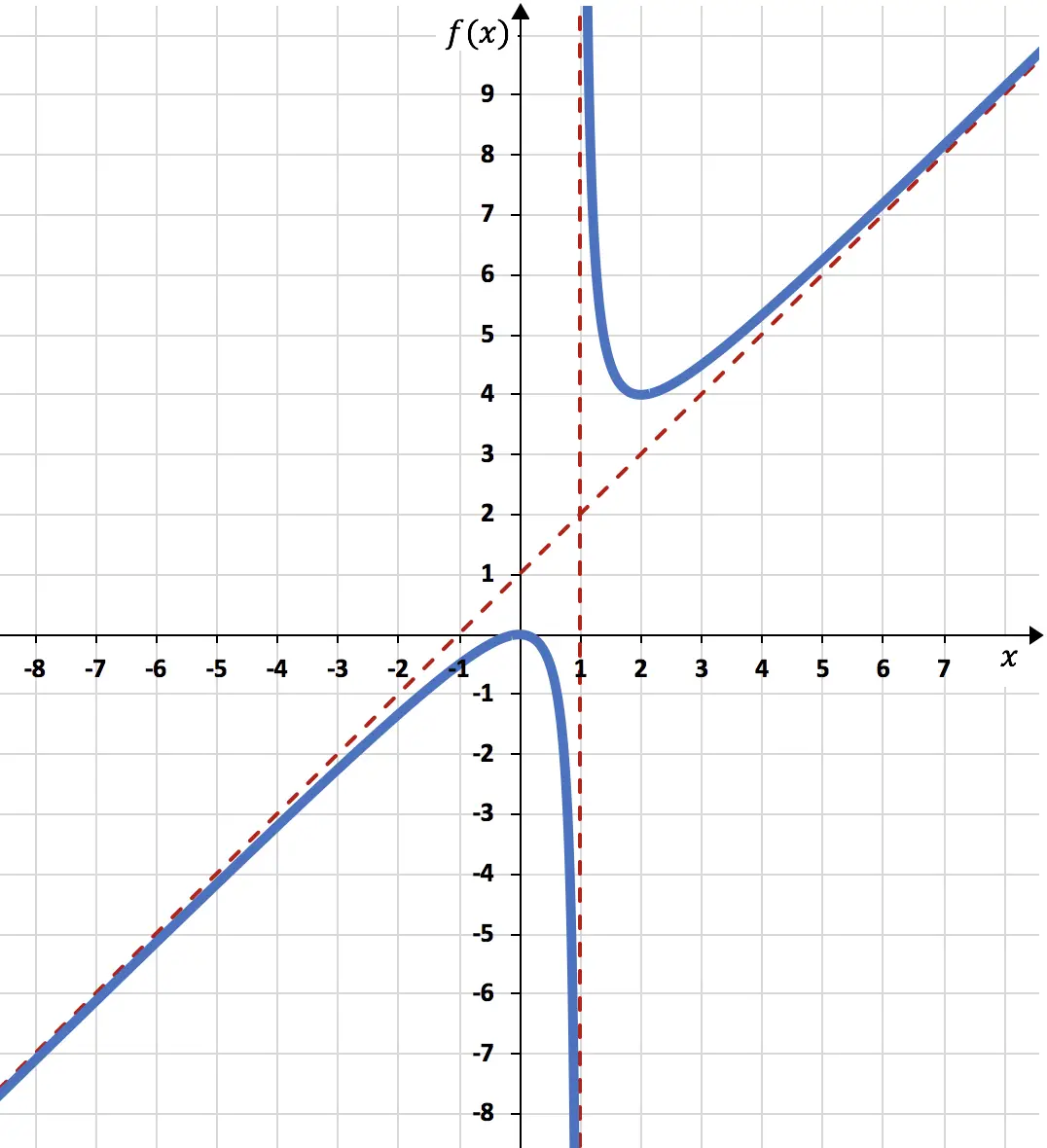
関数を表す演習問題を解決しました
演習 1
次の多項式関数をグラフにします。
![]()
最初に行うことは、関数の定義域を計算することです。これは多項式関数であるため、ドメインは実数のみで構成されます。
![]()
X 軸との交点を見つけるには、次のように解きます。
![]()
![]()
![]()
これは 2 より大きい次数の方程式です。したがって、方程式を因数分解します。
![]()
したがって、x=-1 が解となります。そして、結果として得られる二次方程式を解くことで他の解を計算します。
![Rendered by QuickLaTeX.com \begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e79a2a2f6650c4095c0dca52188c40c3_l3.png)
したがって、X 軸との交点は次のようになります。
![]()
そして
![]()
そして、Y 軸との交点を見つけるために、次のように計算します。
![]()
Y 軸上の x は常に 0 であるため、次のようになります。
![]()
したがって、Y 軸との交点は次のようになります。
![]()
関数に垂直方向の漸近線があるかどうかを確認するには、領域に属さない点での関数の極限を計算する必要があります。この場合、ドメインにはすべての実数が含まれます。したがって、この関数には垂直方向の漸近線がありません。
一方、関数の水平方向の漸近線は、関数の無限極限の結果になります。まだ:
![]()
関数の無限限界により +∞ が得られるため、この関数には水平方向の漸近線がありません。
次に、斜めの漸近線を計算します。斜めの漸近線は次の形式になります。
![]()
そして
![]()
次の式で計算されます。
![]()
![]()
極限により + ∞ が得られたため、この関数には斜めの漸近線もありません。
関数の単調性を調べるには、まずその導関数を計算する必要があります。
![]()
ここで導関数を 0 に設定し、方程式を解きます。
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d23e2b378508baca9f51117fc8767e90_l3.png)
ここで、得られたすべての特異点、つまり定義域に属さない点 (この場合はすべて属します) と導関数をキャンセルする点 (x=0 および x =2) を数直線上に表します。 :

そして、関数が増加するか減少するかを知るために、各区間の導関数の符号を評価します。したがって、各区間の点 (決して特異点ではない) を取得し、この点で導関数がどのような符号を持つかを調べます。
![]()
![]()
![]()

導関数が正の場合、関数が増加していることを意味し、導関数が負の場合、関数が減少していることを意味します。したがって、成長と衰退の間隔は次のようになります。
成長:
![]()
減少:
![]()
関数は x=0 で増加から減少に向かうため、x=0 が関数の最大値となります。そして、関数は x=2 で減少から増加に変わるため、x=2 が関数の最小値となります。
最後に、見つかった極値を元の関数に代入して、点の Y 座標を求めます。
![]()
![]()
したがって、関数の相対的な極値は次のようになります。
最大オンポイント
![]()
最小点まで
![]()
関数の曲率を調べるために、その二次導関数を計算します。
![]()
次に、二次導関数を 0 に設定し、方程式を解きます。
![]()
![]()
![]()
![]()
見つかったすべての特異点、つまり領域に属さない点 (この場合はすべて属します) と導関数 (x=1) をキャンセルする点を直線上に表します。

そして今度は、関数が凹か凸かを知るために、各区間の二次導関数の符号を評価します。したがって、各区間の点 (決して特異点ではない) を取得し、この点で 2 次導関数がどのような符号を持つかを調べます。
![]()
![]()

二次導関数が正の場合、関数が凸であることを意味します。
![]()
、二次導関数が負の場合、これは関数が凹であることを意味します
![]()
。したがって、凹凸の間隔は次のようになります。
凸型
![]()
:
![]()
凹面
![]()
:
![]()
さらに、関数は x=1 で凹から凸に変化するため、x=1 は関数の変曲点になります。
最後に、見つかった変曲点を元の関数に代入して、点の Y 座標を求めます。
![]()
したがって、関数のターニングポイントは次のとおりです。
分岐点:
![]()
最後に、計算したすべての情報に基づいて、関数をグラフ化します。
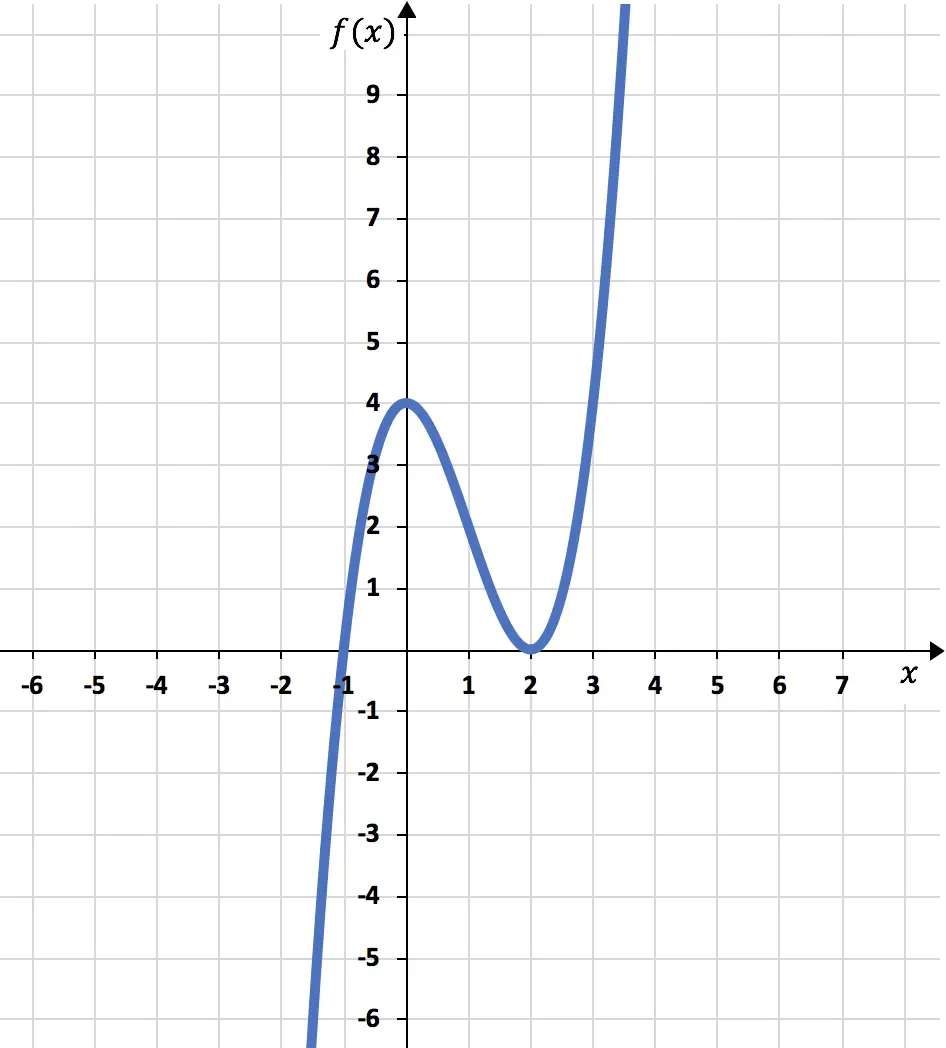
演習 2
次の有理関数をグラフにします。
![]()
関数の定義域を見つけるには、分母を等しく設定します。分数をゼロにして、結果の方程式を解きます。
![]()
![]()
![]()
![]()
![]()
次に、関数の代数式に等しい x 軸を使用して関数のしきい値を決定します。鋼鉄:
![]()
![]()
![]()
![]()
![]()
![]()
負の数には平方根はありません。したがって、関数は X 軸と交差しません。
そして、コンピューターの軸との交点を見つけるために、x=0 で関数を評価します。
![]()
したがって、Y 軸との交点は次のようになります。
![]()
関数に垂直方向の漸近線があるかどうかを確認するには、領域に属さない点 (この場合は x=-1 および x=+1) での関数の極限を計算する必要があります。結果が無限であれば、それは垂直方向の漸近線です。まだ:
![]()
x が -1 に近づくと関数の極限は無限大となるため、x=-1 は垂直漸近線になります。
漸近線 x=-1 に非常に近い数値を関数に代入して、その横限界を計算します。
![]()
![]()
ここで、x=+1 が垂直漸近線であるかどうかを見てみましょう。
![]()
x が +1 に近づくと関数の極限は無限大となるため、x=+1 は垂直方向の漸近線になります。
漸近線 x=1 に非常に近い数値を関数に代入して、その横限界を計算します。
![]()
![]()
一方、関数の水平方向の漸近線は、関数の無限極限の結果になります。まだ:
![]()
関数の無限限界により 1 が得られたため、この関数は y=1 で水平方向の漸近線を持ちます。
この関数には水平方向の漸近線があるため、斜め方向の漸近線はありません。
関数を微分してから、増加と減少の間隔を調べます。
![]()
![]()
ここで導関数を 0 に設定し、方程式を解きます。
![]()
![]()
![]()
![]()
![]()
計算されたすべての臨界点を直線上に表します。これは、領域に属さない点 (x=-1 および x=+1) と導関数をキャンセルする点 (x=0) です。

そして、関数が増加するか減少するかを知るために、各区間の導関数の符号を評価します。したがって、各区間の点 (決して特異点ではない) を取得し、この点で導関数がどのような符号を持つかを調べます。
![]()
![]()
![]()
![]()
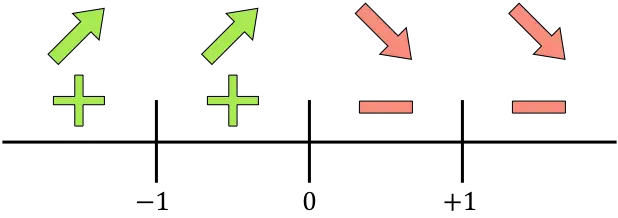
導関数が正の場合は関数が増加し、関数が負の場合は関数が減少します。
成長:
![]()
減少:
![]()
関数は x=0 で増加から減少に向かうため、x=0 は関数の極大値です。
見つかった極値を元の関数に代入して、点の Y 座標を求めます。
![]()
したがって、関数の相対的な極値は次のようになります。
最大オンポイント
![]()
関数の曲率を調べるために、その二次導関数を計算します。
![f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}” title=”Rendered by QuickLaTeX.com”></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-802852beb818dd5a0dce2f30374f3a88_l3.png) すべての用語には、
すべての用語には、
![]()
したがって、分数を単純化できます。
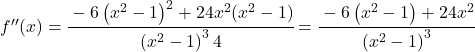
![]()
次に、二次導関数を 0 に設定し、方程式を解きます。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
負の数には平方根はありません。だから一致するポイントがない
![]()
ここで、見つかったすべての特異点、つまり領域に属さない点 (x=-1 および x=+1) と二次導関数をキャンセルする点 (この場合、どれでも):
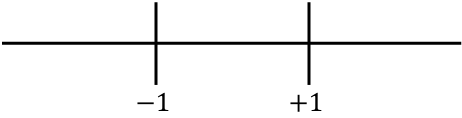
そして、関数が凹か凸かを知るために、各区間の二次導関数の符号を評価します。したがって、各区間の点 (決して特異点ではない) を取得し、この点で 2 次導関数がどのような符号を持つかを調べます。
![]()
![]()
![]()

二次導関数が正の場合、関数が凸であることを意味します。
![]()
、二次導関数が負の場合、これは関数が凹であることを意味します
![]()
。したがって、凹凸の間隔は次のようになります。
凸型
![]()
:
![]()
凹面
![]()
:
![]()
ただし、x=-1 と x=1 では曲率の変化がありますが、これらは変曲点ではありません。なぜなら、それらは機能の領域に属していないからです。
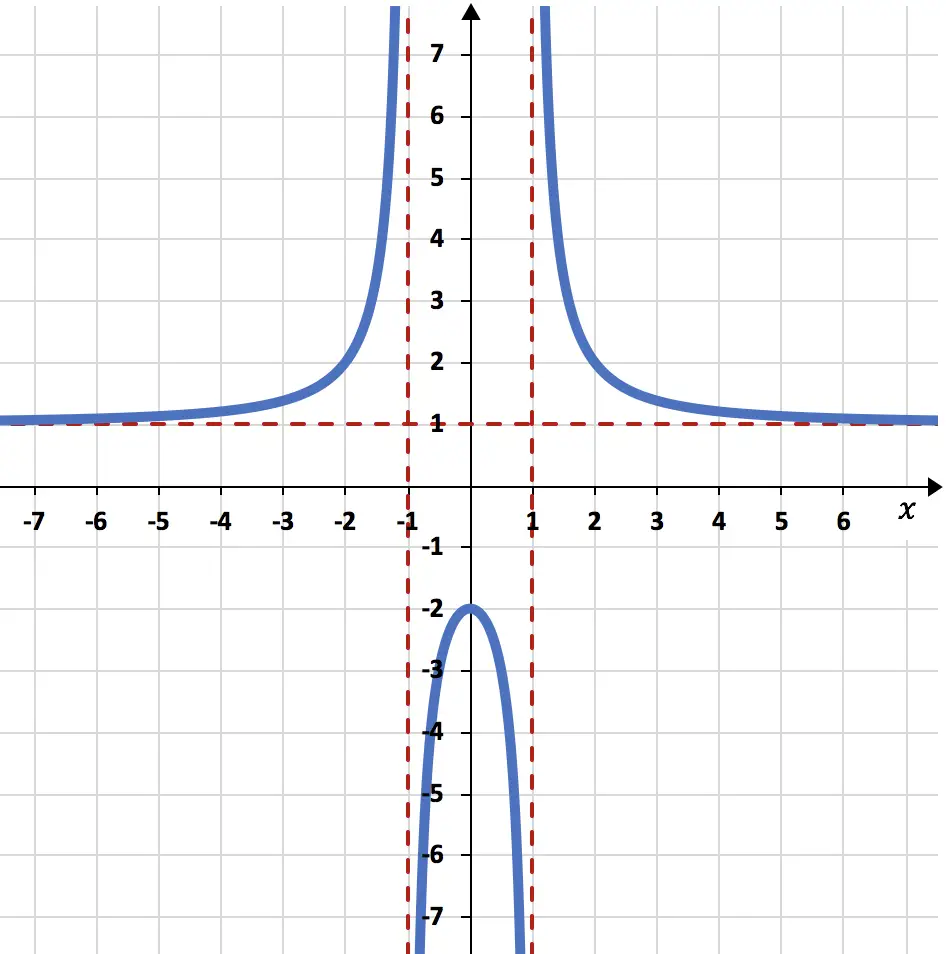
最後に、実行されたすべての計算を使用して関数をグラフにします。
演習 3
次の有理関数をグラフにプロットします。
![]()
これは有理関数であるため、どの数値が関数の定義域に属していないのかを確認するには、分母を 0 に設定する必要があります。
![]()
![]()
![]()
![]()
![]()
X 軸との交点を見つけるには、次のように解きます。
![]()
関数の X 軸の値は常に 0 であるため、次のようになります。
![]()
![]()
![]()
![]()
![]()
したがって、X 軸との交点は次のようになります。
![]()
そして、Y 軸との交点を見つけるために、次のように計算します。
![]()
Y 軸上の x は常に 0 であるため、次のようになります。
![]()
したがって、Y 軸との交点は次のようになります。
![]()
この場合、関数は座標の原点を通過するため、X 軸との交点と Y 軸との交点は一致します。
関数に垂直方向の漸近線があるかどうかを確認するには、領域に属さない点 (この場合は x=-2 および x=+2) での関数の極限を計算する必要があります。結果が無限であれば、それは垂直方向の漸近線です。まだ:
![]()
x が -2 に近づくと関数の極限は無限大となるため、x=-2 は垂直漸近線になります。
漸近線 x=-2 に非常に近い数値を関数に代入して、その横限界を計算します。
![]()
![]()
ここで、x=+2 が垂直漸近線であるかどうかを見てみましょう。
![]()
x が +2 に近づくときの関数の極限は無限大となるため、x=+2 は垂直方向の漸近線になります。
漸近線 x=2 に非常に近い数値を関数に代入して、その横限界を計算します。
![]()
![]()
一方、関数の水平方向の漸近線は、関数の無限極限の結果になります。まだ:
![]()
関数の無限限界により +∞ が得られるため、この関数には水平方向の漸近線がありません。
次に、斜めの漸近線を計算します。斜めの漸近線は次の形式になります。
![]()
そして
![]()
次の式で計算されます。
![]()
![]()
![]()
斜めの漸近線の傾きがわかったら、次の式を使用して切片を決定します。
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-de4326a40acf34b64a28c9da8250bf00_l3.png)
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13478ac6f6fac958ec8b2a714c28bc3d_l3.png)
しかし、不確定性 ∞ – ∞ が得られます。したがって、項を共通の分母に減らす必要があります。これを行うには、x を分数の分母で乗算および除算します。
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e939b43a3405ba644d4b60bb4bacadb_l3.png)
![]()
![]()
つまり、斜線漸近線は次のようになります。
![]()
![]()
![]()
関数の単調性を調べるには、まずその導関数を計算する必要があります。
![]()
![]()
ここで導関数を 0 に設定し、方程式を解きます。
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc1f64cdcd293da4fee1ef02fff9a588_l3.png)
ここで、見つかったすべての特異点、つまり領域に属さない点 (x=-2 および x=+2) と導関数をキャンセルする点 (x=0、x=-) を直線上に表現します。 3.46 および x= +3.46):

そして、関数が増加するか減少するかを知るために、各区間の導関数の符号を評価します。したがって、各区間の点 (決して特異点ではない) を取得し、この点で導関数がどのような符号を持つかを調べます。
![]()
![]()
![]()
![]()
![]()
![]()
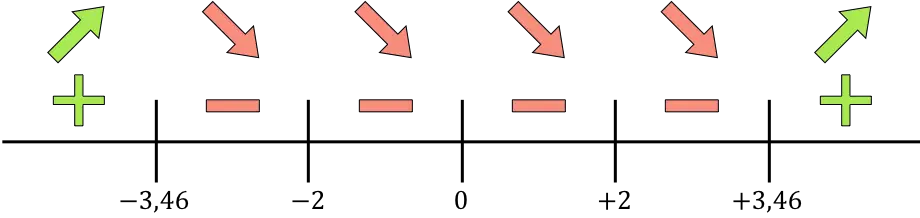
導関数が正の場合、関数が増加していることを意味し、導関数が負の場合、関数が減少していることを意味します。したがって、成長と衰退の間隔は次のようになります。
成長:
![]()
減少:
![]()
関数は x=-3.46 で増加から減少に転じるため、x=-3.46 が関数の最大値になります。そして関数は x=3.46 で減少から増加に転じるので、x=3.46 が関数の最小値となります。
相対的な端の Y 座標を決定します。
![]()
![]()
したがって、関数の相対的な極値は次のようになります。
最大オンポイント
![]()
最小点まで
![]()
関数の曲率を調べるために、関数の二次導関数を計算します。



![]()
![]()
![]()
![]()
次に、二次導関数を 0 に設定し、方程式を解きます。
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31adba554b44aa92fd7227506440ccaf_l3.png)
![]()
実数には負の根がないので解はありません。
ここで、見つかったすべての特異点、つまり領域に属さない点 (x=-2 および x=+2) と二次導関数をキャンセルする点 (x=0) を直線上に表します。

そして、関数が凹か凸かを知るために、各区間の二次導関数の符号を評価します。したがって、各区間の点 (決して特異点ではない) を取得し、この点で 2 次導関数がどのような符号を持つかを調べます。
![]()
![]()
![]()
![]()

二次導関数が正の場合、関数が凸であることを意味します。
![]()
、二次導関数が負の場合、これは関数が凹であることを意味します
![]()
。したがって、凹凸の間隔は次のようになります。
凸型
![]()
:
![]()
凹面
![]()
:
![]()
ただし、x=-2 および x=+2 で曲率の変化がありますが、これらは変曲点ではありません。 x=-2 と x=+2 は関数の定義域に属さないためです。一方、x=0 では曲率の変化 (関数が凸から凹に変化) があり、これは関数に属するため、x=0 は変曲点になります。
見つかった変曲点を元の関数に代入して、変曲点の他の座標を見つけます。
![]()
したがって、関数のターニングポイントは次のとおりです。
分岐点:
![]()
最後に、計算したすべての情報に基づいて、関数を表します。
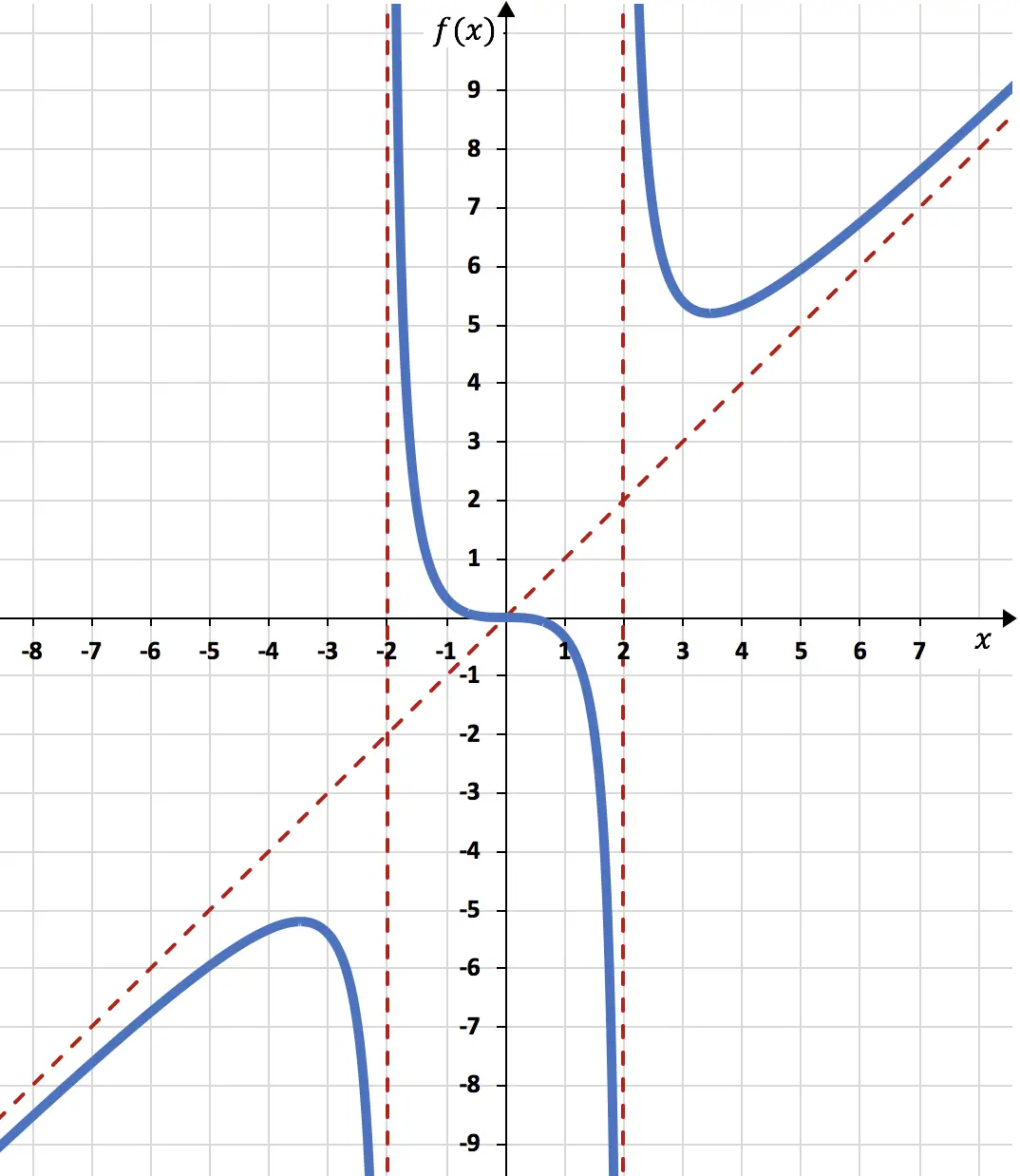
コメント: 関数が点で斜めの漸近線と交差することに注意してください。
![]()
実際、斜線漸近線は、x が +∞ および -∞ に向かう傾向があるときの関数の動作を何よりも決定します。実際、関数はグラフの右側 (x→+∞) およびグラフの左側で斜線漸近線を横切ることはありません。グラフ(x→-∞)。ただし、関数が中央で斜めの漸近線を横切ることは非常にまれであり、非常に特殊なケースです。