ここでは、関数の凹凸とは何か、関数が凹か凸かを判断する方法を学びます。さらに、関数の曲率に関する段階的な演習を行うことができます。
関数の凹凸とは何ですか?
関数の凹凸とは、関数のグラフの曲率を指します。凹関数とは、グラフが山型の関数であり、凸関数とは、グラフが谷型の関数である。
前の段落では、理解を容易にするために凹関数と凸関数を非公式に定義しましたが、凹関数と凸関数の数学的定義は次のとおりです。
- 凹関数:関数の任意の 2 点を結ぶ線分が曲線の下にある場合。
- 凸関数:関数の任意の 2 点を結ぶ線分が曲線の上にある場合。
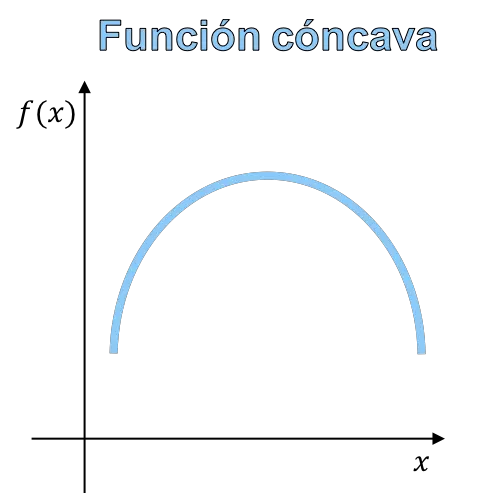

結局のところ、凹関数と凸関数の違いは関数の形状にあるため、関数のグラフから凹と凸を区別することができます。
ただし、関数は必ずしもその領域全体にわたって凹または凸である必要はなく、ある区間では凹、別の区間では凸であることもあります。
注:数学界はまだ完全に同意していないため、一部の教授は反対のことを言っています。彼らは、関数の形状を凹型関数と呼びます。
![]()
、および次の形式を持つ凸関数
![]()
。いずれにせよ、名前が何であれ、重要なことはその機能が何であるかを知ることです。
関数の曲率を研究する方法
関数の曲率を研究するには、関数の凹凸を見つけること、つまり、関数が凹である区間と関数が凸である区間を知ることが含まれます。
したがって、関数の曲率を調べるには、次の手順を実行する必要があります。
- 関数の定義域に属さない点を見つけます。
- 関数の一次導関数と二次導関数を計算します。
- 二次導関数の根を求めます。つまり、次の解を求めて二次導関数を打ち消す点を計算します。
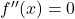
。
- 導関数の根と関数の定義域に属さない点で区間を作成します。
- 各区間の点における二次導関数の値を計算します。
- したがって、二次導関数の符号は、この区間における関数の凹性または凸性を決定します。
- 関数の 2 次導関数が正の場合、関数はこの区間で凸になります。
- 関数の 2 次導関数が負の場合、関数はこの区間で凹型になります。
関数の曲率を求める方法の例
次に、関数の凹凸間隔がどのように計算されるかを確認できるように、例を段階的に解決していきます。
- 次の関数の凹凸を調べます。
![]()
最初に行うことは、関数の定義域を計算することです。この場合、多項式関数があるため、関数の定義域は実数で構成されます。
![]()
関数の定義域を計算したら、関数の 2 次導関数がどの点で消滅するかを調査する必要があります。
したがって、関数の一次導関数を計算します。
![]()
次に、関数の二次導関数を求めます。
![]()
そして、二次導関数を 0 に設定して方程式を解きます。
![]()
![]()
![]()
![]()
関数の定義域を計算したら、
![]()
、ライン上で見つかったすべての重要な点を表します。この場合、関数の定義領域の計算で臨界点は見つかりませんでしたが、関数の 2 次導関数をキャンセルする点が得られました。
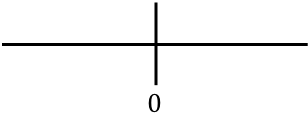
そして今度は、関数が凹か凸かを知るために、各区間の二次導関数の符号を評価します。したがって、各区間の点 (臨界点ではない) を取得し、この点で 2 次導関数がどのような符号を持つかを調べます。
![]()
![]()
![]()

最後に、関数の凹凸間隔を推定します。二次導関数が正の場合、関数が凸であることを意味します。
![]()
、二次導関数が負の場合、これは関数が凹であることを意味します
![]()
。したがって、関数の凹面と凸面の間隔は次のようになります。
凸型
![]()
:
![]()
凹面
![]()
:
![]()
関数の凹凸に関する演習を解決しました。
演習 1
次の多項式関数の凹凸の間隔を計算します。
![]()
演習の関数は多項式であるため、関数の定義域は実数で構成されます。
![]()
関数の定義域を決定したら、それを微分します。
![]()
次に、関数の二次導関数を求めます。
![]()
そして、二次導関数を 0 に設定して方程式を解きます。
![]()
![]()
![]()
![]()
![]()
関数の定義域を計算して解くと、
![]()
、数直線上にあるすべての特異点を表します。

次に、各区間に属する点を取得し、この点で二次導関数がどの符号にあるかを確認してみましょう。
![]()
![]()

二次導関数がゼロより大きい場合、関数が凸であることを意味します。
![]()
ただし、二次導関数が負の場合、これは関数が凹であることを意味します。
![]()
。したがって、凹凸の間隔は次のようになります。
凸型
![]()
:
![]()
凹面
![]()
:
![]()
演習 2
次の有理関数の曲率を調べてください。
![]()
まず関数の定義域を計算する必要があります。これは有理関数であるため、分母をゼロに設定して、どの数値が関数の定義域に属していないかを確認します。
![]()
![]()
![]()
![]()
これは、x が -2 または +2 の場合、分母は 0 になることを意味します。したがって、関数は存在しません。したがって、関数の定義域は、x=-2 と x=+2 を除くすべての数値で構成されます。
![]()
次に、関数の一次導関数を計算します。
![]()
![]()
そして、二次導関数を解きます。


すべての項は次のように乗算されます
![]()
。したがって、分数を単純化できます。

![]()
![]()
![]()
![]()
次に、関数の二次導関数の根を計算しましょう。
![]()
![]()
用語
![]()
これには左側全体を除算する必要があるため、右側全体を乗算できます。
![]()
![]()
共通因数を抽出します。
![]()
乗算が 0 になるには、乗算の 2 つの要素のうちの 1 つがゼロでなければなりません。したがって、各係数を 0 に設定します。
![Rendered by QuickLaTeX.com \displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31adba554b44aa92fd7227506440ccaf_l3.png)
![]()
実数には負の根がないので解はありません。
ここで、得られたすべての臨界点、つまり領域に属さない点 (x=-2 および x=+2) と二次導関数をキャンセルする点 (x=0) を直線上に表します。

そして、関数が凹か凸かを知るために、各区間の二次導関数の符号を評価します。したがって、各区間の点を取得し、その点で二次導関数がどの符号にあるかを調べます。
![]()
![]()
![]()
![]()

二次導関数が正の場合、関数が凸であることを意味します。
![]()
、二次導関数が負の場合、これは関数が凹であることを意味します
![]()
。したがって、凹凸の間隔は次のようになります。
凸型
![]()
:
![]()
凹面
![]()
:
![]()
演習 3
機能
![]()
比較的極端な点がある
![]()
。さらに、関数は凸です
![]()
これと同じ時点で。相対的な極値が最小値であるか最大値であるかを判断します。
➤参照: 関数の最大値と最小値の定義
凸関数を持たせる
![]()
で
![]()
は、この時点の二次導関数が正であることを意味します。つまり、
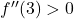 したがって、相対的に極端な場合は、
したがって、相対的に極端な場合は、
![]()
これは最小値です。
![]()
ポジティブですよ。