双曲線余割アーク導関数

この記事では、関数の双曲線逆正割を導出する方法を説明します。双曲逆正割関数の導関数の実際の例も見つかります。

双曲線余割円弧の導関数の公式

x の逆双曲線コセカントの導関数は、x に 1 の平方根と x の 2 乗を足した積で割った負の 1 に等しくなります。

$f(x)=\text{arccsch}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-1}{x\sqrt{1+x^2}}$

したがって、関数の逆双曲線コセカントの微分値は、関数の積に 1 の根を乗じて 2 乗関数を足したもので割った当該関数の微分値を引いたものになります。

$f(x)=\text{arccsch}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1+u^2}}$

要約すると、双曲線逆正割関数の導関数を計算する式は次のようになります。

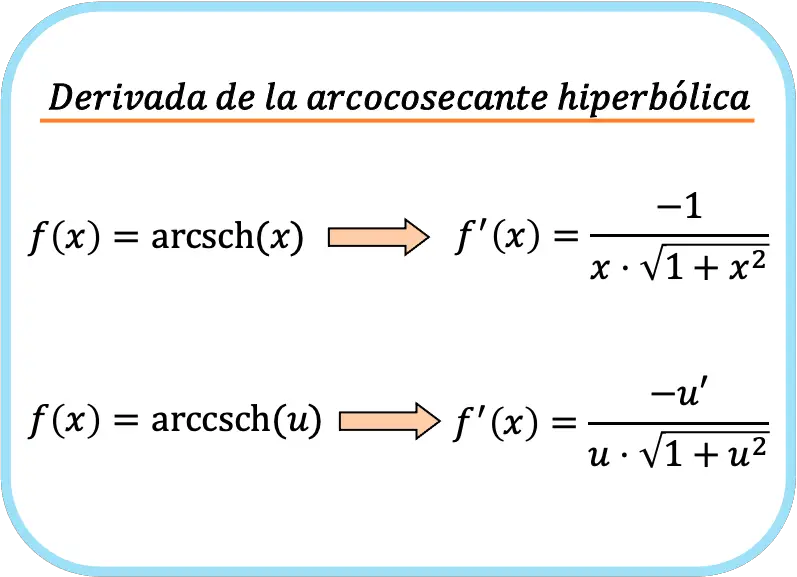
2つの式を入れましたが、両者が異なるというわけではありません。よく見ると、2 番目の式は最初の式と似ていますが、連鎖規則が適用されています。

双曲線余割弧の導関数の例

双曲線逆余割の導関数の公式が与えられた場合、次にそのような関数を 2 つ導出し、それがどのように行われるかを確認します。

例1

$f(x)=\text{arccsch}(3x)$

この演習では、引数に x とは異なる関数があるため、連鎖ルールを使用した円弧双曲線コセカントの導関数の公式を使用する必要があります。

$f(x)=\text{arccsch}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1+u^2}}$

したがって、導関数を見つけるには、u を 3x に置き換え、u’ をその導関数 (3) に置き換える必要があります。

$f(x)=\text{arccsch}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-3}{3x\sqrt{1+(3x)^2}}=\cfrac{-3}{3x\sqrt{1+9x^2}}$

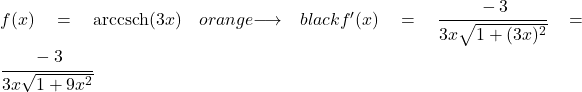
例 2

$f(x)=\text{arccsch}(x^5-2x^3)$

この場合、双曲線逆正割引数に多項式関数があるため、それを導出するために連鎖規則も使用する必要があります。

$f(x)=\text{arccsch}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1+u^2}}$

そこで、引数関数の導関数を分数の分子に置き、分母では多項式関数によって u を変更します。

$\begin{aligned}f(x)=\text{arccsch}(x^5-2x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(5x^4-6x^2)}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\\[1.5ex] &=\cfrac{-5x^4+6x^2}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\end{aligned}$

双曲線余割アーク導関数

双曲線余割円弧の導関数の公式

双曲線余割弧の導関数の例

例1

例 2

類似商品

コメントする返信をキャンセル

双曲線余割円弧の導関数の公式

双曲線余割弧の導関数の例

例1

例 2

類似商品

コメントする 返信をキャンセル

コメントする返信をキャンセル