双曲線正割導関数

この記事では、関数の双曲線正割を導出する方法を説明します。双曲線正割の導関数の公式と、このタイプの導関数のいくつかの実際の例が見つかります。

双曲線正割の導関数の公式

x の双曲線正割の導関数は、x の双曲線正接と x の双曲線正割の積を引いた値に等しくなります。

$f(x)=\text{sech}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(x)\cdot \text{tanh}(x)$

したがって、関数の双曲線正割の導関数は、関数の双曲線正割と関数の双曲線正接と前記関数の導関数の積を引いたものになります。

$f(x)=\text{sech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(u)\cdot \text{tanh}(u)\cdot u'$

つまり、双曲線正割関数の導関数の公式は次のとおりです。

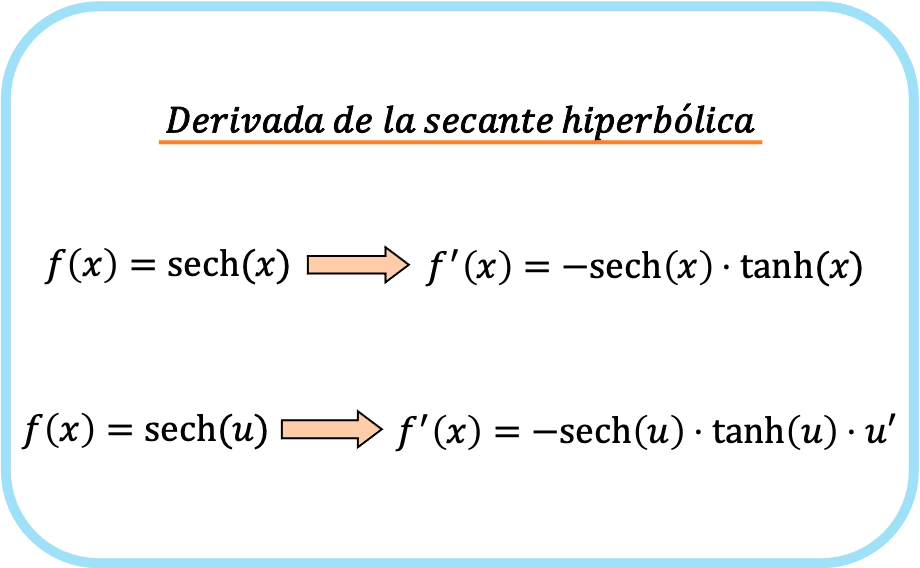
実際には両方の式が 1 つの式に属していることに注意してください。唯一の違いは、2 番目の式では連鎖規則が適用されることです。

双曲線正割の導関数の公式がわかったので、このタイプの三角関数の導関数のいくつかの演習を解いていきます。

$f(x)=\text{sech}(2x)$

この例では、双曲線正割引数に x とは異なる関数があるため、それを導出するには連鎖律公式を使用する必要があります。

$f(x)=\text{sech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(u)\cdot \text{tanh}(u)\cdot u'$

関数 2x は線形であるため、その導関数は 2 です。したがって、導関数を求めるには、式内の u を 2x に、u’ を 2 に置き換えるだけです。

$f(x)=\text{sech}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(2x)\cdot \text{tanh}(2x)\cdot 2$

$f(x)=\text{sech}(x^2)$

双曲線割線の引数には別の機能があるため、この演習の機能は複合的です。したがって、双曲線正割公式と連鎖律を使用して、その導出を行う必要があります。

$f(x)=\text{sech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(u)\cdot \text{tanh}(u)\cdot u'$

x を 2 に累乗すると 2x が得られるため、x の 2 乗の双曲線正割の導関数は次のようになります。

$f(x)=\text{sech}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(x^2)\cdot \text{tanh}(x^2)\cdot 2x$