双曲線正弦の微分

ここでは、双曲線正弦（公式）を導出する方法を説明します。さらに、双曲線サイン導関数の解決例がいくつか表示されます。最後に、このタイプの三角関数の導関数の公式を証明します。

ハイパボリックサインから導出される式

x の双曲線正弦の導関数は、x の双曲線余弦です。

$f(x)=\text{senh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x)$

したがって、関数の双曲線サインの導関数は、関数の双曲線余弦とその関数の導関数の積に等しくなります。

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

実際、上の 2 つの式は同じです。唯一の違いは、2 番目の式では連鎖律を適用することです。 x の導関数は 1 なので、関数は変わりません。

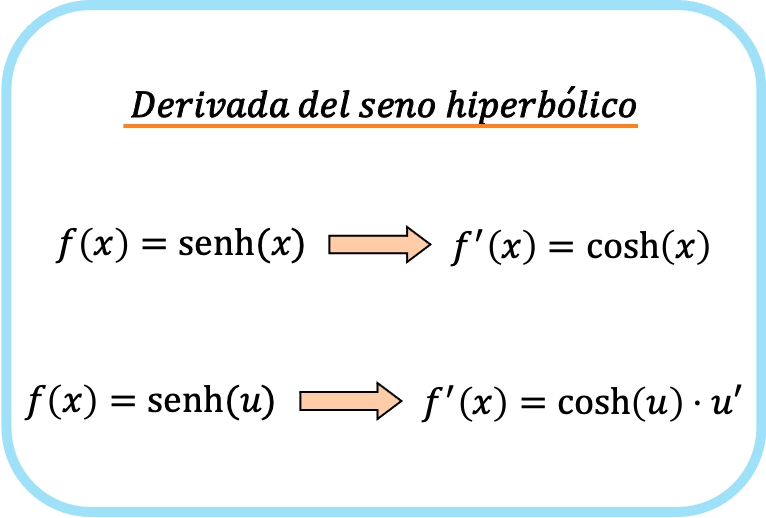
ご覧のとおり、双曲線サイン微分の公式は、サイン微分の公式と非常によく似ています。

双曲線正弦導関数の公式が何であるかをすでに理解したら、次に双曲線正弦導関数のいくつかの例を解いてみましょう。したがって、これがどのように行われるかについては、確かに疑問の余地はありません。

$f(x)=\text{senh}(2x)$

この場合、双曲線正弦引数には x とは異なる関数があるため、導関数を見つけるには連鎖律を備えた双曲線正弦導関数の式を使用する必要があります。

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

2x の導関数は 2 であるため、2x の双曲線正弦の導関数は、2x に 2 を掛けた双曲線余弦になります。

$f(x)=\text{senh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(2x)\cdot 2=2\text{cosh}(2x)$

$f(x)=\text{senh}(x^2)$

双曲線正弦関数の導関数の式は次のとおりです。

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

一方、二次関数 x ²の導関数は 2x です。したがって、関数全体の導関数は次のようになります。

$f(x)=\text{senh}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x^2)\cdot 2x$

最後に、双曲線正弦導関数の公式を示します。これを行うには、双曲線サインの数学的定義から始めます。

$\text{senh}(x)=\cfrac{e^x-e^{-x}}{2}$

ここで、等式の 2 つの辺を推定します。

$\displaystyle\bigl(\text{senh}(x)\bigr)'=\left(\frac{e^x-e^{-x}}{2}\right)'$

方程式の右辺を導出するには、除算の導関数の公式を使用します。

$\displaystyle\text{senh}'(x)=\frac{(e^x+e^{-x})\cdot 2}{2^2}=\frac{e^x+e^{-x}}{2}$

そしてまさに、双曲線余弦を定義する式に到達しました。したがって、双曲線正弦の導関数は次のように証明されます。

$\displaystyle\text{senh}'(x)=\text{cosh}(x)$