この記事では、関数の逆正弦を導出する方法を説明します。関数の逆正弦の導関数の例があり、ステップごとに解いた演習で練習することもできます。最後に、逆正弦微分公式のデモンストレーションもご覧ください。
逆正弦の導関数は何ですか?
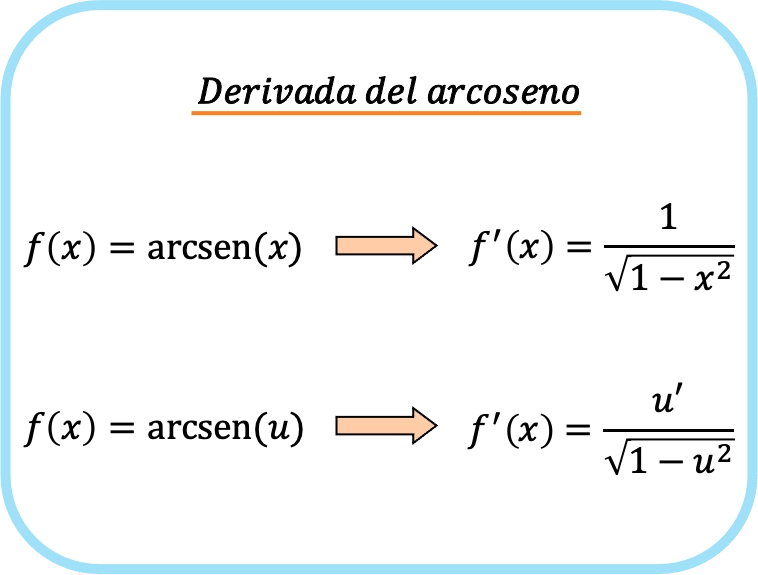
x の逆正弦導関数は、1 の平方根から x の 2 乗を引いたものです。
![]()
したがって、関数の逆正弦の微分値は、その関数の微分値を 1 の平方根で割った商から関数の 2 乗を引いたものに等しくなります。
![]()
論理的には、2 番目の式は最初の式に連鎖則を適用することで得られます。
逆正弦は正弦の逆関数であるため、逆正弦とも呼ばれます。
逆正弦微分の例
逆正弦導関数の公式を確認した後、このタイプの三角関数導関数の例をいくつか説明します。こうすることで、関数の逆正弦がどのように導出されるのかを理解しやすくなります。
例 1: 2x の逆正弦の導関数
![]()
逆正弦関数の導関数を見つけるには、対応する式を使用する必要があります。
![]()
したがって、2x の導関数は 2 なので、2x の逆正弦導関数は、2 を 1 の根から 2x の 2 乗を引いた値で割ったものとなります。
![]()
例 2: x の 2 乗の逆正弦の導関数
![]()
逆正弦微分公式を使用してそれを導き出します。
![]()
関数 x 2は 2 次であるため、その導関数は 2x です。したがって、x の逆正弦の 2 乗の導関数は次のようになります。
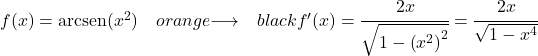
例 3: e xの逆正弦の導関数
![]()
この例の関数は複合関数であるため、導関数を解くために連鎖規則を適用する必要があります。
![]()
e xの導関数はそれ自体であるため、関数全体の導関数は次のようになります。
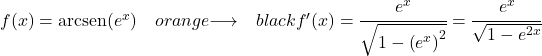
逆正弦微分で解決された問題
次の逆正弦関数を導出します。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
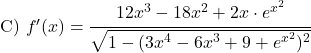
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) } f'(x)& =\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a82c0fd18a8672100ed3b79525a1028_l3.png)
逆正弦微分公式の証明
次に、逆正弦の導関数の公式の数学的証明に進みます。
![]()
まず、逆正弦を正弦に変換します。
![]()
次に、方程式の両辺を微分します。
![]()
私たちはあなたをクリアします:
![]()
次に、基本的な三角恒等式を適用します。
![]()
![]()
そして、上で x が y の正弦と同等であると推定したように、等価性は維持されます。
![]()
ご覧のとおり、この手順を適用すると、逆正弦関数の導関数の式が得られ、式が満たされることが示されます。