水平漸近線 - マソリティ

この記事では、関数の水平漸近線とは何か、およびその計算方法について説明します。さらに、概念を完全に理解するためにこのタイプの漸近線の例がいくつかあり、さらに、水平漸近線の解決済み演習で練習することもできます。

水平漸近線とは何ですか?

関数の水平漸近線は、そのグラフが決して交差することなく無限に近づく水平線です。したがって、水平漸近線の方程式はy=kになります。ここで、 kは水平漸近線の値です。

つまり、 x が無限大に近づくときの関数の限界がkに等しい場合、 kは水平漸近線になります。

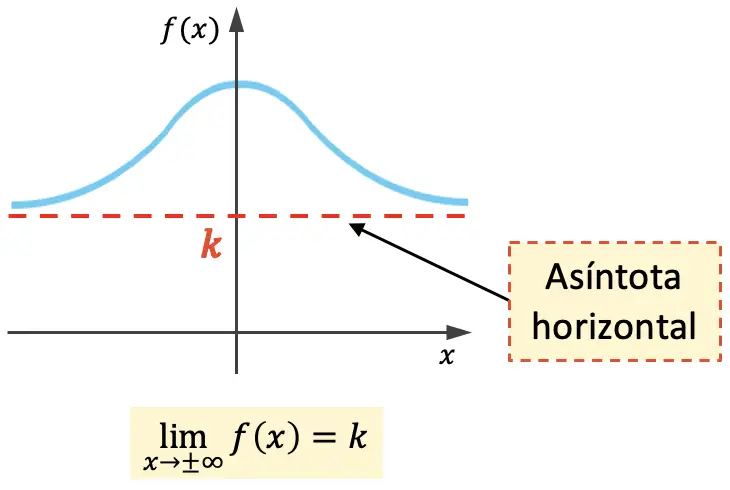
上記の関数にはグラフの両側に水平漸近線がありますが、関数は片側にのみ水平漸近線を持つことができます。

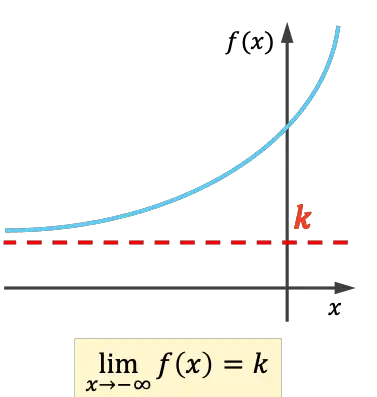
少なくとも無限大までの制限が実数を与える場合、この関数は左水平漸近線を持ちます。
プラス無限大までの制限が実数を与える場合、この関数は右に水平漸近線を持ちます。

関数の水平漸近線を計算する方法

関数の水平漸近線を計算するには、次の手順に従う必要があります。

関数の無限大 (+∞ および -∞) の極限を計算します。
無限大への制限が実数 (k) を与える場合、直線 y=k は関数の水平漸近線になります。
どちらの限界も実数に対応しない場合、関数には水平方向の漸近線がありません。

水平漸近線の例

これがどのように行われるかの例を見ることができます。次の有理関数からすべての水平漸近線を削除します。

$f(x)=\cfrac{x+1}{x-1}$

水平方向の漸近線を決定するには、関数のマイナス無限大とプラス無限大での極限を計算する必要があります。

$\displaystyle \lim_{x \to +\infty} \cfrac{x+1}{x-1} = \cfrac{+\infty}{+\infty}= \cfrac{1}{1} = \bm{1}$

$\displaystyle \lim_{x \to -\infty} \cfrac{x+1}{x-1} = \cfrac{-\infty}{-\infty}= \cfrac{1}{1} = \bm{1}$

➤参照: 無限間の無限不確定性を解決する方法

無限大における 2 つの極限は 1 を与えるため、 y=1 が関数の唯一の水平漸近線になります。

以下は関数をグラフで表したものです。ご覧のとおり、関数は (プラス無限大とマイナス無限大の両方で) y=1 に非常に近づきますが、水平漸近線であるため、それに触れることがありません。

注:一部の特殊なケースでは、関数は 1 つ以上の点で水平漸近線と交差しますが、一般に、関数のグラフがその漸近線を交差することはありません。

一方、この関数には x=1 の垂直方向の漸近線もあります。グラフからわかるように、x=1 の線に非常に近づきますが、その値には決して到達しないからです。

水平漸近線の問題を解決しました

演習 1

次の分数関数の水平漸近線がある場合は、それを見つけます。

$\displaystyle f(x)= \frac{4x+3}{2x-1}$

解決策を参照

有理関数の水平漸近線を決定するには、関数の無限大における極限を計算する必要があります。

$\displaystyle \lim_{x \to +\infty} \frac{4x+3}{2x-1} = \frac{4(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{4}{2} = \bm{2}$

$\displaystyle \lim_{x \to -\infty} \frac{4x+3}{2x-1} = \frac{4(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{4}{2} = \bm{2}$

この場合、分子と分母が同じ次数であるため、不定形式 ∞/∞ の結果は、最高次数の x の係数の除算になります。

関数のプラス無限大とマイナス無限大での極限は 2 となるため、 y=2 は水平方向の漸近線であり、関数が持つ唯一の漸近線です。

演習 2

根を持つ次の有理関数のすべての水平漸近線を見つけます。

$\displaystyle f(x)= \frac{3x}{\sqrt{x^2+2}}$

解決策を参照

関数の水平漸近線を見つけるには、まず正の無限大での極限を計算します。

$\displaystyle \lim_{x \to +\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{+\infty}{+\infty} = \frac{3}{\sqrt{1}} = \bm{3}$

次に、関数の極限を負の無限大まで解きます。

$\displaystyle \lim_{x \to -\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{-\infty}{+\infty} = \frac{-3}{\sqrt{1}} = \bm{-3}$

➤ 無限への制限がどのように解決されたかについて疑問がある場合は、無限間の無限不確定性を解決する方法に関する上記のリンクを確認することをお勧めします。

この場合、無限遠の限界の 2 つの異なる値が得られました。したがって、関数には 2 つの水平漸近線があります。y=3 は右側の関数の水平漸近線であり、一方、y=-3 は左側の関数の水平漸近線です。

演習 3

次の区分的に定義された関数の水平漸近線を計算します。

$\displaystyle f(x)=\left\{ \begin{array}{lcl}\displaystyle\frac{3x-1}{x^2}& \text{si} & x<4\\[4ex]\displaystyle\frac{x^3-2x+5}{2x^3-9} & \text{si} & x\geq 4 \end{array} \right.$

解決策を参照

関数の水平方向の漸近線を計算するための公式はありませんが、プラス無限大とマイナス無限大までの限界を計算する必要があります。

したがって、少なくとも無限の制限を見つけるには、最初のセクションで定義された関数を使用します。

$\displaystyle \lim_{x \to -\infty}\frac{3x-1}{x^2}= \frac{-\infty}{+\infty}=\bm{0}$

したがって、線 y=0 は関数の左側の水平漸近線です。

次に、2 番目のセクションで定義された関数を使用して、プラス無限大での制限を計算します。

$\displaystyle \lim_{x \to +\infty}\frac{x^3-2x+5}{2x^3-9}= \frac{+\infty}{+\infty}=\mathbf{\frac{1}{2}}$

したがって、線 y=1/2 は関数の右側の水平漸近線です。

水平漸近線とは何ですか?

関数の水平漸近線を計算する方法

水平漸近線の例

水平漸近線の問題を解決しました

演習 1

演習 2

演習 3

コメントする 返信をキャンセル

コメントする返信をキャンセル