無限(∞/∞)間の無限不確定性

この記事では、無限大間の不確定性の無限大(∞/∞)を計算する方法を説明します。多項式、根数、指数関数など、あらゆる種類の関数を使用したこの不決定の例が見つかります。さらに、無限間の無限不定を与える限界を段階的に解決する演習でトレーニングすることができます。

無限間の無限不確定性を解決する方法

関数の極限が無限大を無限大で割ったとき、それは不確定性 (または不確定形式) であることを意味します。無限大間の不確定性を無限大にする関数の極限を解くには、分子多項式の次数を分母多項式の次数と比較する必要があります。

$\displaystyle\lim_{x\to +\infty}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\frac{+\infty}{+\infty}$

不確定性無限を無限で割った結果は、分数の分子の次数と分母の次数によって異なります。

分子多項式の次数が分母多項式の次数より小さい場合、不確定性の無限大を無限大で割った値はゼロに等しくなります。
分子多項式の次数が分母多項式の次数と等しい場合、無限大にわたる無限不確定性は 2 つの多項式の主要係数の商になります。
分子多項式の次数が分母多項式の次数より大きい場合、無限大間の不確定性の無限大は多かれ少なかれ無限大を与えます (符号は 2 つの多項式の主項に依存します)。

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> <h2 class=$ 無限間の無限不定の例

各ケースのいくつかの例を見て、無限間の不定形無限がどのように解決されるかを見てみましょう。

分子の次数が分母の次数より小さい

上で見たように、分子多項式の次数が分母多項式の次数より小さい場合、無限大間の無限不定極限は常に 0 になります。

例 1:

$\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

分子の多項式は 2 次であり、分母の多項式は 3 次であるため、極限の解は 0 になります。

例 2:

$\displaystyle \lim_{x \to -\infty} \frac{-7x}{2x^4+3x^2}=\frac{-7\cdot (-\infty)}{2(-\infty)^4}=\frac{+\infty}{+\infty}= \bm{0}$

分子の多項式関数は 1 次ですが、分母の関数は 4 次であるため、負の無限大の制限は 0 です。

分子の次数が分母の次数に等しい

分子多項式の次数が分母多項式の次数と等しい場合、不定限界無限×無限は、2 つの多項式の先頭係数 (高次項の係数) を除算することによって計算されます。

例 3:

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

この場合、2 つの多項式は 2 次であるため、より高次の項の係数を除算して正の無限大での極限を見つける必要があります。

例 4:

$\displaystyle \lim_{x \to -\infty} \cfrac{2x+1}{5x+3} = \cfrac{2(-\infty)}{5(-\infty)}= \cfrac{-\infty}{-\infty} =\cfrac{\bm{2}}{\bm{5}}$

x が無限大をマイナスする傾向があるときが限界ですが、無限大間の無限不確定性も同様に解決されます。

分子の次数が分母の次数より大きい

分子多項式の次数が分母多項式の次数より大きい場合、無限大間の無限大の不定形は常に無限大を与え、無限大の符号は 2 つの多項式の高次項によって決まります。

例 5:

$\displaystyle \lim_{x \to +\infty} \cfrac{x^2+7}{x-2} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

分子の関数は分母の関数よりも高い次数を持っているため、無限大の不確定性無限大は無限大を与えます。また、この場合、分子と分母の両方が正の無限大になるため、制限の結果も正になる必要があります。

例6:

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

この問題では、二乗項はいずれも正であるため、分子からは正の無限大が得られますが、分母からは負の無限大が得られます。したがって、正を負で割った値は負に等しいため、結果の制限は負になります。

無限と根の間の無限不確定性

多項式関数がある場合に、無限間の無限不確定性を計算する方法を説明しました。しかし…根がある場合、無限は無限でどれだけ除算されるでしょうか?

無理関数 (根のある関数) の次数は、主項の次数と根号の指数との商です。

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

したがって、根を持つ関数の極限によって infinity 間の不確定性が生じる場合、上で説明したのと同じルールを分子と分母の次数に適用する必要がありますが、根を持つ多項式の次数は異なる方法で計算されることを考慮に入れてください。

根号を使用した関数の無限大への制限の次の例を見てください。

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

分子の次数は 2、分母の次数は 4 (8/2=4) であり、分子の次数が分母の次数より小さいため、制限は 0 になります。

一方、分子と分母の次数が等しい場合、不定極限を計算するには、根号で主係数を取得する必要があります。

$\displaystyle\lim_{x\to +\infty}\frac{6x-5}{\sqrt{9x^2+2x}}=\frac{6(+\infty)}{\sqrt{9(+\infty)^2}}=\frac{+\infty}{+\infty}=\frac{6}{\sqrt{9}}=\frac{6}{3}=\bm{2}$

無限と指数関数間の無限不確定性

最後に、無限大の不確定商のケースを研究するだけで済みます。つまり、無限大と指数関数の間の無限不確定性はどのくらいになるのかということです。

指数関数の増加は多項式関数の増加よりもはるかに大きいため、指数関数の次数が多項式関数の次数よりも大きいことを考慮する必要があります。

$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”> したがって、無限不定性を無限で割った結果が指数関数の極限に起因する場合は、分子と分母の次数について説明したのと同じ規則を適用するだけで十分ですが、指数関数は多項式より高次であることを考慮してください。。 さらに、割り算の分子と分母に指数関数がある場合、底が大きい指数関数の次数が高くなります。 <p class=$ $\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

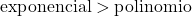
この場合、分母は指数関数で形成されるため、分子よりも高次になります。したがって、無限間の不定形無限は消滅する。

無限間の無限不確定性の演習を解決しました

演習 1

次の有理関数の極限を計算します。

$\displaystyle\lim_{x \to +\infty} \cfrac{6x-5}{x^2-1}$

解決策を参照

極限を計算すると、無限大間の無限不確定性が得られますが、分子の次数が分母の次数よりも小さいため、不確定極限はゼロに等しくなります。

$\displaystyle \lim_{x \to +\infty} \cfrac{6x-5}{x^2-1} = \cfrac{6(+\infty)}{(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{0}$

演習 2

次の不定極限を解きます。

$\displaystyle\lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4}$

解決策を参照

極限を計算しようとすると、不確定性 ∞/∞ が得られます。この場合、分子多項式の次数は分母多項式の次数より大きいため、不定極限はプラス無限大に等しくなります。

$\displaystyle \lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4} = \cfrac{(+\infty)^3}{5(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{+\infty}$

演習 3

次の極限を無限大で解きます。

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

解決策を参照

この制限により、プラス無限大の間に不確定マイナス無限大が生じます。分子の次数は分母の次数より大きいため、不定極限はプラス無限大に等しくなります。ただし、除算は負の無限大×正の無限大であるため、結果はマイナス無限大になります。

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

演習 4

次の不定極限を解きます。

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

解決策を参照

この問題では、無限大にわたる無限不定形式は、同じ次数の 2 つの多項式の商から得られるため、不定極限の結果は、それらの主係数の除算になります。

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

演習 5

次の制限を少なくとも無限大まで計算します。

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

解決策を参照

分子の代数式の次数は分母の式の次数より小さいため、不確定性 +∞/+∞ は 0 を返します。

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

演習 6

ルートを使用して、次の関数の不定極限を解きます。

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

解決策を参照

分子の式は根号の下にあるため、次数は 7/3 です。一方、分母の多項式は2次になります。そして、7/3>2 であるため、この制限はプラスの無限大を与えます。

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=+\infty$

演習 7

分数を使用して、次の関数の無限大の制限を決定します。

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

解決策を参照

この演習では、分子の次数が分母の次数より大きい不確定性マイナス無限大をマイナス無限大で割った値が得られます。したがって、次のようになります。

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

演習 8

次の関数の少なくとも無限大までの極限を求めます。

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

解決策を参照

分母多項式は 2 次であり、分子多項式は 1 次です。したがって、不確定性の無限大を無限大で割ると 0 になります。

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

演習 9

次の関数の少なくとも無限の極限を解きます。

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

解決策を参照

分子の次数が分母より大きいため、不定形 ∞/∞ の結果は無限大になります。さらに、正を負で割ると負になるため、無限大記号は負になります。

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

演習 10

無限間の無限不確定性を使用して次の極限を解きます。

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

解決策を参照

指数関数は多項式関数より高次であるため、極限は無限大になります。ただし、正を負で割ると、無限大の符号は負になります。

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

演習 11

次の制限を計算します。

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2}$

解決策を参照

この問題では、無限大の不確定性無限は、2 つの多項式の支配的な係数を除算することによって解決されます。これは、それらが同じ次数であるためです。

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2} = \cfrac{(-\infty)^3}{-(-\infty)^3} = \cfrac{-\infty}{-(-\infty)}= \cfrac{-\infty}{+\infty}=\cfrac{1}{-1}=\bm{-1}$

演習 12

x が無限大に近づくときの次の関数の極限を解きます。

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}$

解決策を参照

分子の未知数は直接二乗されませんが、注目すべき恒等式を解くと、分子の次数が分母の次数よりも大きいことが明らかにわかります。まだ：

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}=\lim_{x \to +\infty} \cfrac{x^2+9+6x}{x} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

演習 13

次の関数の無限大の極限を立方根で計算します。

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}$

解決策を参照

分子は立方根で構成されているため、次数は 3/3=1 になります。この場合、分子の次数は分母の次数と等しいため、無限大間の無限不確定性は次のように解決されます。

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}= \cfrac{\sqrt[3]{8(+\infty)^3}}{-4(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt[3]{8}}{-4}=\cfrac{2}{-4}=\bm{-}\mathbf{\cfrac{1}{2}}$

演習 14

2 つの根号を使用して、次の関数の無限極限を解きます。

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

解決策を参照

分子の次数は 7/3 = 2.33、分母の次数は 5/2 = 2.5 です。したがって、分子の次数が分母の次数より小さいため、無限の間の不定無限極限は 0 になります。

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

演習 15

次の制限を計算します。

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

解決策を参照

分子の次数に関係なく、分母に指数関数があるため、無限大に対する不定形式の無限大の結果は 0 になります。

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

無限間の無限不確定性 (∞/∞)

無限間の無限不確定性を解決する方法

分子の次数が分母の次数より小さい

例 1:

例 2:

分子の次数が分母の次数に等しい

例 3:

例 4:

分子の次数が分母の次数より大きい

例 5:

例6:

無限と根の間の無限不確定性

無限と指数関数間の無限不確定性

無限間の無限不確定性の演習を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

演習 6

演習 7

演習 8

演習 9

演習 10

演習 11

演習 12

演習 13

演習 14

演習 15

コメントする返信をキャンセル

無限間の無限不確定性を解決する方法

分子の次数が分母の次数より小さい

例 1:

例 2:

分子の次数が分母の次数に等しい

例 3:

例 4:

分子の次数が分母の次数より大きい

例 5:

例6:

無限と根の間の無限不確定性

無限と指数関数間の無限不確定性

無限間の無限不確定性の演習を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

演習 6

演習 7

演習 8

演習 9

演習 10

演習 11

演習 12

演習 13

演習 14

演習 15

コメントする 返信をキャンセル

コメントする返信をキャンセル