多項式関数 - マソリティ

ここでは、多項式関数とは何か、およびすべての種類の多項式関数とは何かを説明します。さらに、多項式関数の性質についても説明します。

多項式関数とは何ですか?

多項式関数は、その代数式が多項式である関数です。つまり、多項式関数は、次数の異なる有限数の項の加算または減算によって定義されます。

したがって、多項式関数は次の式で数学的に記述されます。

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

一方、多項式関数は次の式を使用して定義することもできます。

$\displaystyle f(x)=\sum_{k=0}^{n}a_k\cdot x^k$

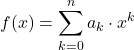
条件はどこにありますか

$a_k$

そして

$x^k$

はそれぞれ、多項式関数を形成する各単項式の係数と変数です。

用語

$a_nx^n$

は主項と呼ばれ、関数の最高次数の単項式であるため、多項式関数の次数を示します。つまり、最大値の指数が多項式関数の次数を示す指数になります。

以下で多項式関数の特徴をさらに見ていきますが、多項式関数の定義域はすべて実数です。

多項式関数の種類

多項式関数の定義を考慮して、すべての種類の多項式関数がどのようなものであるかを見てみましょう。

定数関数

定数関数は0次の多項式関数なので、独立変数(x)のどの値に対しても常に同じイメージをとる関数の一種です。

定数関数の一般式は次のとおりです。

$f(x)=k$

たとえば、次の 3 つの関数は定数または次数 0 の多項式関数です。

$f(x)=5 \qquad f(x)=2 \qquad f(x)=-3$

定数関数のグラフィック表現は、定数に等しい値を持つ水平線 (X 軸に平行) です。

このタイプの関数に関するその他の機能については、次のリンクで確認できます。

➤参照:定数関数の特性

一次関数

線形関数は、アフィン関数とも呼ばれ、一次多項式関数です。したがって、このタイプの多項式関数は、線形項と独立項でのみ構成できます。

$f(x)=mx+n$

金

$m$

は線の傾きであり、

$n$

は y 切片、つまり関数が Y 軸と交差する場所です。

線形関数または 1 次多項式関数の例:

$f(x)=4x+3\qquad f(x)=-5x$

関数の項にがあるかどうかに応じて、線形関数とアフィン関数を区別する人もいます。

$n$

切片のあるアフィン関数と切片のない線形関数であるかどうか。

一次関数のグラフ表現は常に直線であり、その傾きの程度は関数の傾きの値に依存します。

以下に、一次多項式関数をグラフで示します。

$f(x)=2x-1.$

ただし、一次関数をグラフ化するには、いくつかの概念について理解しておく必要があります。次のリンクでは、このタイプの多項式関数をグラフ化する方法について段階的に説明しています。

➤参照: 一次関数のグラフ表示

二次関数

二次関数は 2 次の多項式関数、つまり高次項が 2 次の関数です。

したがって、二次関数の公式は次のようになります。

$f(x)=ax^2+bx+c$

金

$ax^2$

は二次項、

$bx$

線形項と

$c$

多項式関数の独立項。

二次関数または二次多項式関数の例:

$f(x)=5x^2+2x-1\qquad f(x)=-2x^2+x+7$

二次関数のグラフは常に放物線であり、その形状は先頭の係数の符号によって異なります。

$a:$

係数が
$a$

が正の場合、二次関数は凸になります (次のような形状になります)

$\bm{\cup}$

）。
代わりに、係数が
$a$

が負の場合、二次関数は凹型になります (次のような形状になります)

$\bm{\cap}$

）。

したがって、2 次多項式関数の主係数の符号を使用して、そのグラフが取る形状を知ることができますが、その正確なグラフ表現を作成するには、特定の手順に従う必要があります。この手順は次のリンクで確認できます。

➤参照:2 次関数のグラフ表示

3次関数

3 次関数は3 次の多項式関数です。したがって、このタイプの多項式関数は代数的に次のように表現されます。

$f(x)=ax^3+bx^2+cx+d$

3 次関数または 3 次多項式関数の例:

$f(x)=x^3+4x^2+5x-1$

$f(x)=2x^3-3x^2+9$

3 次関数のグラフ表現は 3 次曲線に対応します。ただし、この種の関数をグラフで表現するには、複雑な手順 (導関数を含む) に従う必要があります。それがどのように行われるかはここで見ることができます:

➤参照:関数の表現方法

ご覧のとおり、多項式には無限の項を含めることができるため、多項式関数の種類は実際には無限です。たとえば、4 次関数は 3 次関数に似ていますが、2 次項が追加されています。重要なことは、多項式関数の種類が関数の次数によって区別されることを理解することです。

多項式関数の性質

多項式関数には次の特徴があります。

多項式関数の定義域は実数のセットです。

$\text{Dom } f=\mathbbf{R}$

すべての多項式関数は連続です。

1 より大きい次数の多項式関数には漸近線がありません。

多項式関数のタイプに関係なく、縦軸 (Y 軸) との唯一の交点は、その独立項の高さ、つまり次の点にあります。

$(0,a_0)$

一方、多項式関数は、最大でも関数の次数と同じ回数だけ横軸 (X 軸) を切ります。

多項式関数に偶数次の項しかない場合、これはそれが OY 軸に関して対称であることを意味します。一方、多項式関数に奇数次の項しかない場合、これは関数が座標の原点に関して対称であることを意味します。

多項式関数の相対極値 (最大または最小) の数は、最大でも関数の多項式の次数から 1 を引いた値になります。

多項式関数の変曲点の数は、最大でも関数の多項式の次数から 2 を引いた値に等しくなります。

演算は多項式関数を使用して実行できます。
- 2 つの多項式関数の合計により、別の多項式関数が得られます。
- 2 つの多項式関数の積により、別の多項式関数が生じます。
- 多項式関数にスカラー (実数) を乗算すると、同様の多項式関数が生成されますが、そのグラフは縮小または拡大されます。
- 2 つの多項式関数の合成は、別の多項式関数と等しくなります。