関数の対称性: 対称関数と非対称関数

この記事では、対称関数 (偶数関数と奇数関数) とは何か、および関数の対称性を調べる方法について説明します。また、これらのタイプの関数のプロパティを確認することもでき、最終的には、対称関数を段階的に解決する演習を行うことができます。

対称関数とは何ですか?

対称関数とは、グラフ表現に対称軸が見られる関数です。対称関数には、Y 軸に関して対称な偶数関数と、座標の原点に関して対称である奇数関数の 2 種類があります。

対称軸とは、対向する点が互いに等距離になるように、何かを 2 つの部分に分割する想像上の線であることを思い出してください。

偶数関数

偶数関数は、y 軸に関して対称な関数です。つまり、Y 軸は関数の対称軸です。

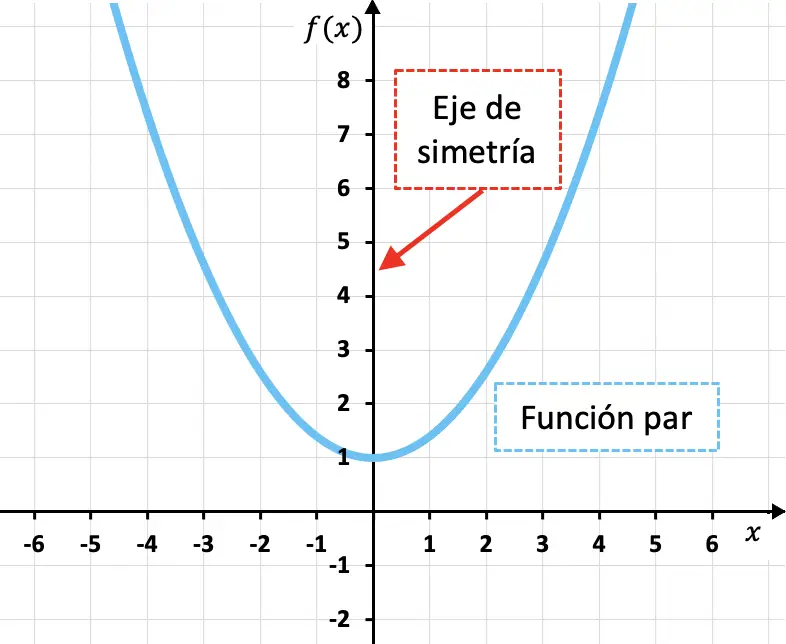
上に示した二次関数でわかるように、独立変数 (x) の任意の値に対する偶数関数のイメージは、反対の値 (-x) に対する関数のイメージと等価です。つまり、数学的には、次の条件を満たす関数は偶数です。

$f(x)=f(-x)$

偶数関数は対称関数の一種です。奇数関数がどのようなものかを見てみましょう。

奇数関数

奇関数は、座標の原点、つまり点 (0,0) に対して対称な関数です。

以下に、奇数関数のグラフを示します。

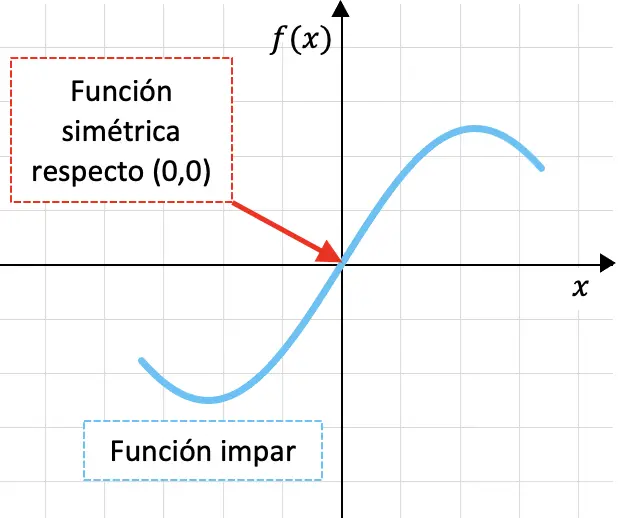
関数が座標原点に関して対称であるという事実は、関数のグラフを最初に OY 軸を通って折り、次に OX 軸を通って折り畳むと、関数のグラフが重なることを意味します。

代数的には、関数のイメージ間に次の関係が満たされる場合、その関数は奇数です。

$f(-x)=-f(x)$

関数の対称性を知ることは、グラフの半分だけを知っていれば他の部分をすぐに描くことができるため、それを表現するのに非常に役立ちます。

関数の対称性を見つける方法

関数の対称性を調べるには、次の画像を計算する必要があります。

$-x$

、つまり計算する必要があります。

$f(-x).$

したがって、画像の結果に応じて、関数の対称性は次のようになります。

満たされていれば
$f(-x)=f(x)$

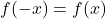
、関数は偶数であるため、 Y 軸に関して対称です。
満たされていれば
$f(-x)=-f(x)$

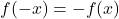
、関数は奇数であるため、座標の原点に関して対称です。
上記の条件がいずれも満たされない場合、それは非対称関数です (対称軸がありません)。

たとえば、次の 3 次関数の対称性を分析してみましょう。

$f(x)=x^3$

関数の対称性を調べるために、次のように計算します。

$f(-x):$

$f(-x)=(-x)^3=-x^3$

結果の代数式は、元の関数式と等価ですが、符号が変更されています。つまり、次の等式が満たされます。

$f(-x)=-f(x)$

したがって、この関数は奇数であり、座標の原点 (0,0) に関して対称です。

対称関数の性質

対称関数には次の特徴があります。

2 つの偶数/奇数関数の合計は、別の偶数/奇数関数と等しくなります。
2 つの偶数関数または 2 つの奇数関数の積により、偶数関数が得られます。
偶数/奇数関数の導関数は偶数/奇数関数です。
2 つの偶数/奇数関数間の合成は、偶数/奇数関数と同等です。
偶数と奇数の両方である唯一の関数、つまり OY 軸と原点に関して対称な関数は次の関数です。
$f(x)=0.$

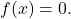
関数の対称性の問題を解決しました

演習 1

次の関数の対称性を求めます。

$f(x)=x^4+5x^2$

解決策を参照

関数の対称性を計算するには、次を評価する必要があります。

$f(-x):$

$f(-x)=(-x)^4+5(-x)^2=x^4+5x^2$

負の数値を累乗すると正の数値が得られるため、この場合、次の方程式が成り立ちます。

$f(-x)=f(x)$

したがって、関数は偶数であり、したがって y 軸 (Y 軸) に関して対称です。

演習 2

次の有理関数の対称性を調べてください。

$f(x)=\cfrac{7x^2}{3+x^3}$

解決策を参照

関数の対称性を判断するには、次のようにします。

$f(-x):$

$f(-x)=\cfrac{7(-x)^2}{3+(-x)^3}=\cfrac{7x^2}{3-x^3}$

この問題では、次の画像があるため、対称条件は満たされません。

$-x$

に等しくありません

$f(x)$

もしない

$-f(x).$

$f(-x)\neq f(x)\neq -f(x)$

したがって、この関数には対称軸がなく、むしろ非対称関数となります。

演習 3

次の関数の対称性を計算します。

$f(x)=2x|x|$

解決策を参照

関数の対称性を分析するには、次の計算を行う必要があります。

$f(-x):$

$\begin{aligned}f(-x)&=2(-x)|(-x)|\\[2ex]&=-2x|-x|\\[2ex]&=-2x|x|\\[2ex]&=-(2x|x|)\\[2ex]&=-f(x)\end{aligned}$

この場合、結果の式は元の式と似ていますが、符号が変更されているため、次の式が満たされます。

$f(-x)=-f(x)$

したがって、この関数は奇数であり、座標の原点 (0,0) に関して対称です。

対称関数とは何ですか?

偶数関数

奇数関数

関数の対称性を見つける方法

対称関数の性質

関数の対称性の問題を解決しました

演習 1

演習 2

演習 3

コメントする 返信をキャンセル

コメントする返信をキャンセル