双曲線正弦関数

7月 4, 2023

この記事では、双曲線正弦に関するすべてを説明します。その公式、そのグラフィック表現、そのすべての特性、他の関数との関係など。

双曲線正弦の公式

双曲線サイン関数は、主要な双曲線関数の 1 つであり、記号sinh(x)またはsinh(x)で表されます。双曲線正弦は、e ^xから e ^{-x を}引いて 2 で割った値に等しくなります。

したがって、双曲線正弦の式は次のようになります。

$\displaystyle\text{senh}(x)=\cfrac{e^{x}-e^{-x}}{2}$

したがって、双曲線サインは指数関数に関係します。

➤参照:指数関数の特性

双曲線正弦のグラフ表示

前のセクションで見た式を使用して、双曲線正弦値の表を作成し、関数をグラフ化できます。

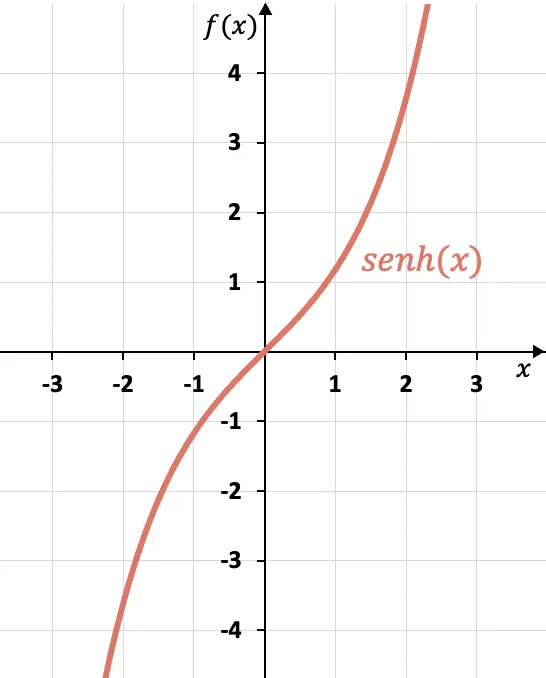
双曲線正弦

このグラフでは、反対側の x が反対のイメージを持っているため、双曲線サインが奇関数であることがわかります。つまり、双曲線サイングラフは座標の原点 (0, 0) に関して対称です。

ご覧のとおり、双曲線サイングラフは、周期関数であるサインのグラフとは大きく異なります。次のリンクで、サインのグラフィック表現と双曲線サインとのすべての違いを確認できます。

➤参照:サイン関数のグラフ表示

ハイパボリックサインの特徴

双曲線正弦には次の特性があります。

ハイパボリックサイン関数の定義域はすべて実数です。

$\text{Dom } f = \mathbb{R}$

ハイパボリックサイン関数の範囲もすべて実数です。

$\text{Im } f= \mathbb{R}$

双曲線正弦は連続的な奇関数です。

$\displaystyle \text{senh}(-x) =- \text{senh}(x)$

同じ交点、つまり座標原点で X 軸と Y 軸を切ります。

$(0,0)$

x がプラス/マイナス無限大になる傾向がある場合の双曲線正弦関数の極限は、プラス/マイナス無限大と等しくなります。

$\displaystyle\lim_{x\to+\infty}\text{senh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{senh}(x)=-\infty$

双曲線正弦はドメイン全体で厳密に増加しているため、最大値も最小値もありません。

ただし、点 x = 0 で曲率が変化するため、それが関数の変曲点になります。 x=0 より小さい値の場合は凹関数であり、x=0 より大きい値の場合は凸関数です。

双曲線サイン関数の導関数は双曲線余弦です。

$f(x)=\text{senh}(x) \ \longrightarrow \ f'(x)=\text{cosh}(x)$

同様に、双曲線サイン関数の積分は双曲線余弦です。

$\displaystyle \int \text{senh}(x) \ dx= \text{cosh}(x) + C$

双曲線正弦関数のテイラー級数は次の式と等価です。

$\displaystyle\text{senh}(x)=x+\cfrac{x^3}{3!}+\cfrac{x^5}{5!}+\cfrac{x^7}{7!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n+1}}{(2n+1)!}$

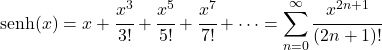
双曲線正弦関数のラプラス変換は次のとおりです。

$\mathcal{L}\bigl[\text{senh}(at)\bigr]=\cfrac{a}{s^2-a^2}$

ハイパボリックサインの数学的関係

双曲線サインは、次の方程式によって他の双曲線関数にリンクされます。

基本方程式は、双曲線サインを双曲線余弦に関連付けます。

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

したがって、双曲線サイン関数と双曲線余弦関数は、双曲線方程式、つまり x ² -y ² =1 によって関係付けられます。円方程式 (x ² +y ² =1) で結び付けられる三角関数のサイン関数やコサイン関数とは異なります。

サイン、コサイン、タンジェントの双曲線関数は、次の方程式で関連付けられます。

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

一方、2 つの異なる数値の加算または減算の双曲線サインは、次の式で計算できます。

$\text{senh}(x+y)=\text{senh}(x)\text{cosh}(y)+\text{senh}(y)\text{cosh}(x)$

$\text{senh}(x-y)=\text{senh}(x)\text{cosh}(y)-\text{senh}(y)\text{cosh}(x)$

数値の 2 倍の双曲線正弦は、次の数学的関係を適用することで決定できます。

$\text{senh}(2x)=2\text{senh}(x)\text{cosh}(x)$

2 つの双曲線正弦の合計または減算は、次の式を使用して求めることができます。

$\displaystyle\text{senh}(x)+\text{senh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{senh}(x)-\text{senh}(y)=2\text{senh}\left(\frac{x-y}{2}\right)\text{cosh}\left(\frac{x+y}{2}\right)$

最後に、双曲線正弦の 2 乗は、次の式を適用して計算できます。

$\text{senh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)-1\Bigr)$

コメントする返信をキャンセル