この記事では、関数の周期性とは何かについて説明します。さらに、周期関数の例がいくつか表示されます。最後に、三角関数の最も重要な特性の 1 つである三角関数の周期を分析します。
関数の周期性とは何ですか?
関数の周期性は、値を周期的に繰り返す関数の特性です。つまり、グラフが一定の間隔ごとに繰り返される場合、その関数は周期的です。この間隔をピリオドと呼びます。
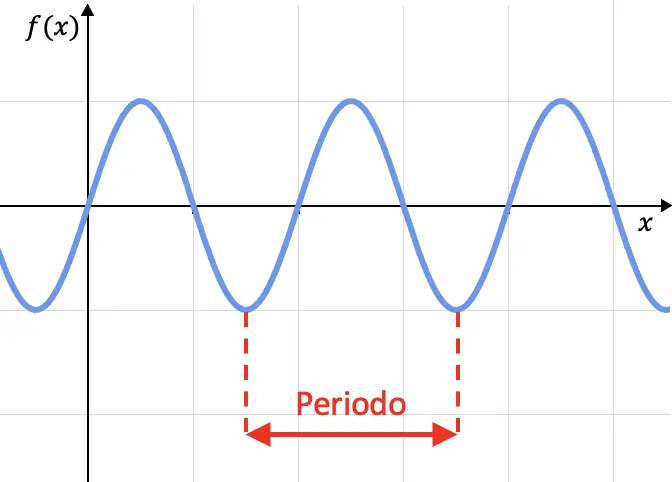
数学的には、関数が満たされるだけの場合、その関数は周期的であると定義されます。
![]()
独立変数 x の任意の値に対して。
![]()
ここで、 T は周期関数 i kの周期です。
関数の周期性の例
関数の周期性の概念を理解したら、関数の周期性を計算する方法の例をいくつか見ていきます。
例1
次の関数が周期的かどうかを判断します。
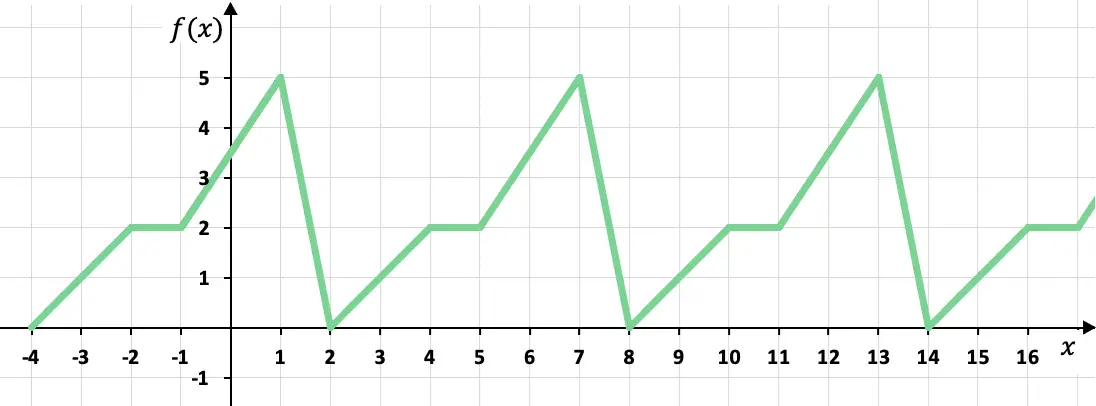
この区分的に定義された関数は、グラフの値が周期的に繰り返されるため、周期関数です。より正確には、この関数は 6 x ごとに同じ値を取るため、関数の周期は 6 に等しくなります。
![]()
例 2
次の関数の周期性を求めます。
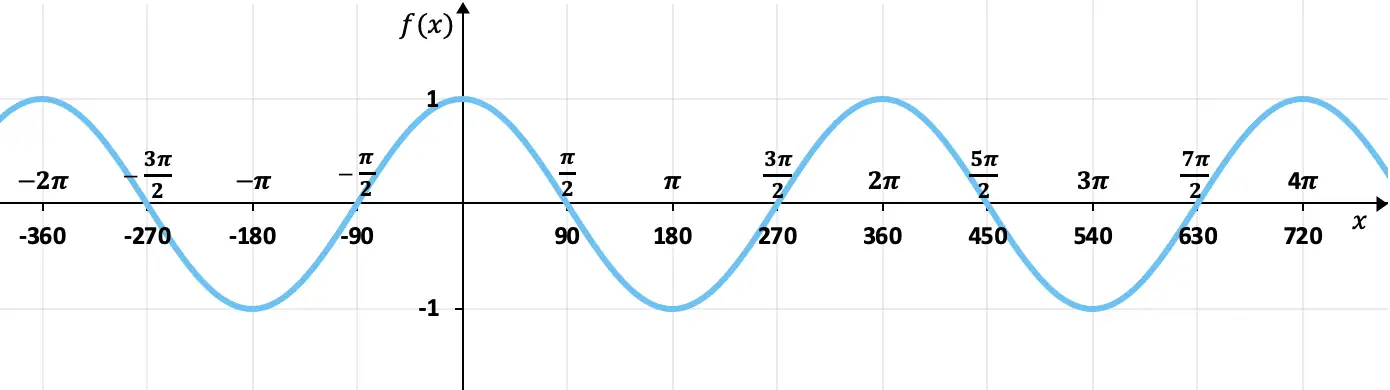
この関数は、三角関数、より正確にはコサイン関数のグラフィック表現に対応します。
グラフからわかるように、関数は値を周期的に繰り返すため、周期関数です。さらに、波のピークとピークの間には 2π (または 360 度) のスペースがあるため、これが関数の周期になります。
![]()
三角関数の周期性
周期性と三角関数は密接に関係しており、実際、このタイプの関数の主な特徴の 1 つは、ほとんどの三角関数が周期的であることです。
次に、3 つの主要な三角関数、サイン、コサイン、タンジェントの周期性を調べます。
正弦関数周期
サイン関数の式は次のとおりです。
![]()
この場合、周期を求めるために関数をグラフ化する必要はありませんが、次の式を適用するだけで簡単に計算できます。
![]()
さらに、サイン関数には、周期を変更するとグラフの形状も変更されるという特殊性があります。次のリンクで、期間の値がグラフ表示にどのような影響を与えるかを確認できます。
➤参照:サイン関数のグラフ
コサイン関数の周期
コサイン関数の代数式は次のとおりです。
![]()
サインと同様に、コサイン関数の周期は次の公式を使用して直接求めることができます。
![]()
コサイン期間の値によってグラフが完全に決まります。次のリンクをクリックして理由を調べてください。
➤参照:コサイン関数のグラフ
正接関数の周期
正接関数は数学的に説明されます。
![]()
正接関数の周期は、サインおよびコサインの周期と同じ式で計算されます。
![]()
ただし、正接関数グラフには周期的に繰り返す漸近線があるため、サインやコサインとは異なります。この三角関数のこの機能とその他の機能については、次のリンクで確認できます。
➤参照:正接関数のグラフ