このページでは、反比例関数とは何か、またそのグラフの作成方法について説明します。さらに、このタイプの関数のすべての特性、その定義域の計算方法、さらにいくつかの例と練習問題が段階的に解決されています。
反比例関数とは何ですか?
反比例関数は、2 つの反比例する量を関連付ける関数です。つまり、一方の量が減少すると他方の量が増加し、その逆も同様です。一般に、反比例関数は次の式で定義されます。
![]()
金
![]()
は比例比と呼ばれる定数です。
したがって、反比例関数は常に分母に 1 次多項式を含む分数で構成されます。したがって、これらは有理関数の一種です。
反比例関数の例:
![]()
一般的に
![]()
は一般に独立変数であり、
![]()
従属変数、つまり変数
![]()
による
![]()
一方、比例比 (分子項) は正または負の場合があり、その符号は関数の増加または減少を示します。
- 定数の場合

が負の場合、関数は増加しています。
- 代わりに、定数の場合、

がプラスの場合、機能は低下しています。
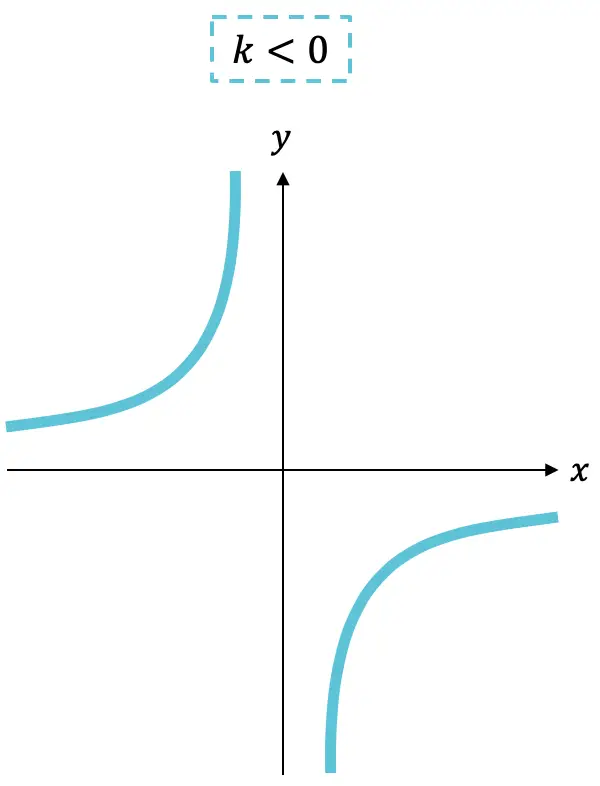
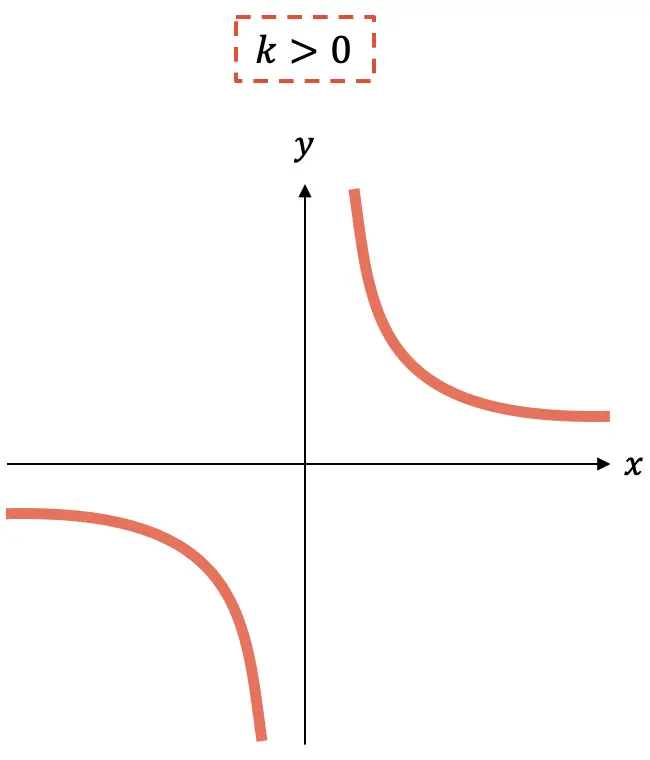
ご覧のとおり、反比例関数のグラフは常に2 つの双曲線で構成されており、これらはkの符号に応じて 1 つの象限または別の象限に存在します。
反比例関数の定義域
有理関数の一種である反比例関数の定義域は、分母から消えるものを除いてすべて実数です。分母がゼロになることはなく、無限大になるためです。
例として、次の反比例関数の定義域を決定します。
![]()
分母がいつゼロになるかを知るには、その式を 0 に等化し、方程式を解く必要があります。
![]()
![]()
したがって、x が 1 の値を取ると、分母は 0 になり、不確定性が得られます。したがって、関数の定義域はすべて実数からマイナスしたものになります。
![]()
![]()
逆比例関数をグラフ化する方法
例を使用して反比例関数をグラフ化する方法を見てみましょう。
- 次の関数をグラフで表します。
![]()
最初に行う必要があるのは、関数のドメインを見つけることです。分数であるため、分母を 0 にすることはできません。その場合、無限大になるからです。したがって、分母をキャンセルした場合を除き、定義域はすべて x になります。
したがって、どの x がドメインに属していないのかを確認するために、分母を 0 に設定します。
![]()
![]()
したがって、関数の定義域は 2 を除くすべての数値になります。
![]()
どの数値がドメインに属していないのかがわかったら、値のテーブルを作成します。反比例の関数を表すには、領域 (2) に属さない数値の左側に 3 または 4 ポイント、右側に 3 または 4 ポイントを計算する必要があります。
![]()

次に、グラフ上の点を表してみましょう。
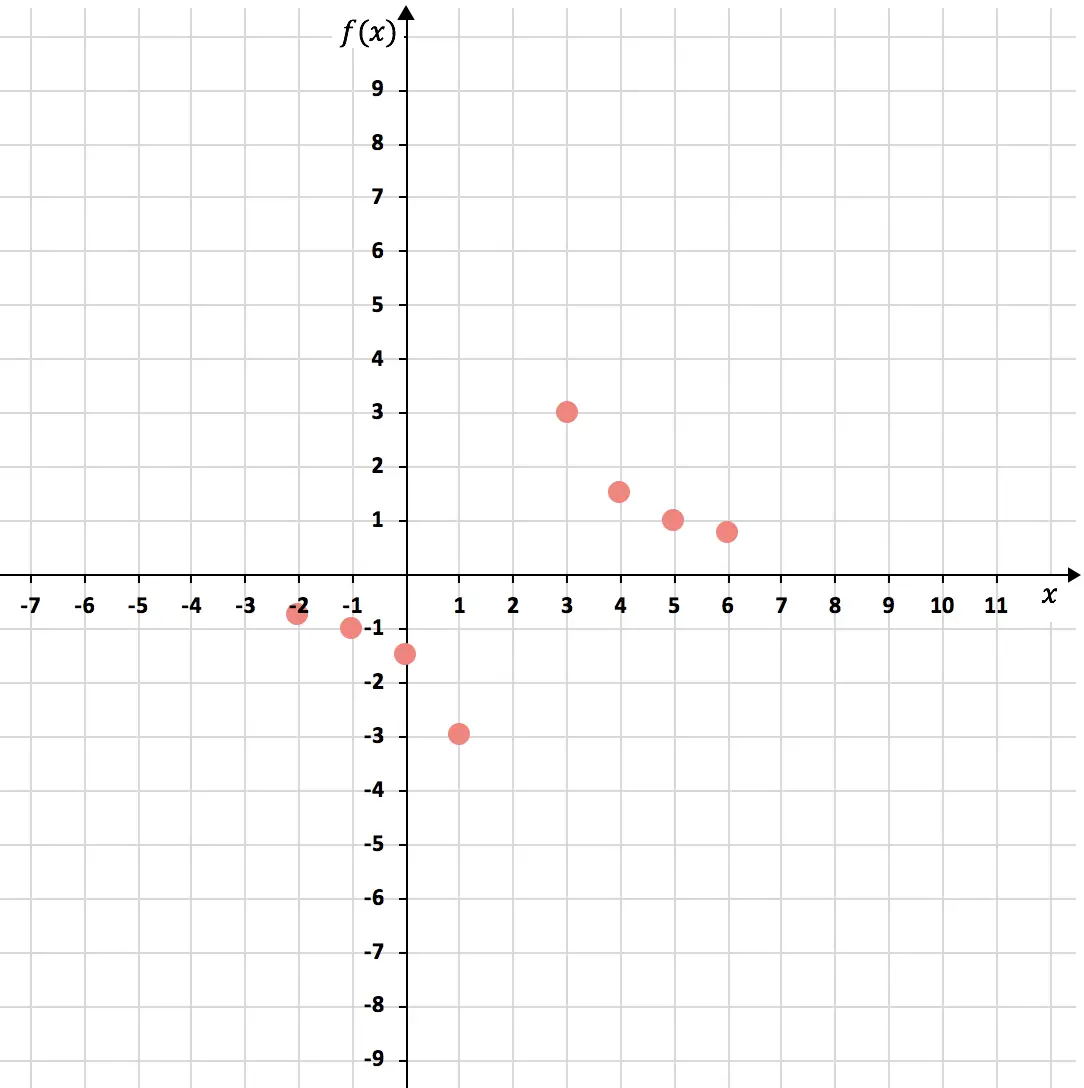
そして最後に点を結合して、反比例関数の 2 つの双曲線を形成します。さらに、双曲線の枝を長くして、成長し続けることを示します。

関数は次のように近似することに注意してください。
![]()
、右側と左側の両方にあります。ただし、2 に完全に到達することはなく、非常に近づいていますが、到達することはありません。それで、
![]()
それは垂直方向の漸近線です。その理由は
![]()
は関数のドメインに属していないため、その時点では関数は存在しません。
同じことが水平 X 軸でも起こります。関数は次のように近似します
![]()
しかし決して触らないでください。まだ、
![]()
は水平漸近線です。
これは、反比例関数には常に漸近線があるため、すべての反比例関数は不連続であることを意味します。
関数の漸近線と限界について詳しくは、当社の Web サイトをご覧ください。
反比例関数の問題を解決しました
演習 1
次の反比例関数の定義域を計算します。
![]()
分母が 0 の場合、反比例関数は存在しません。その場合、関数は ∞ を生成するからです。したがって、x が分母をキャンセルし、したがって定義域に属さないことを確認するには、関数の分母を 0 に設定する必要があります。
![]()
![]()
![]()
![]()
演習 2
次の反比例関数をグラフにします。
![]()
最初に行うことは、関数の定義域を計算することです。
![]()
![]()
どの数値がドメインに属していないのかがわかったら、次の関数を使用して値の配列を作成します。

最後に、得られた点をグラフ上に表して双曲線を描き、反比例関数を形成します。
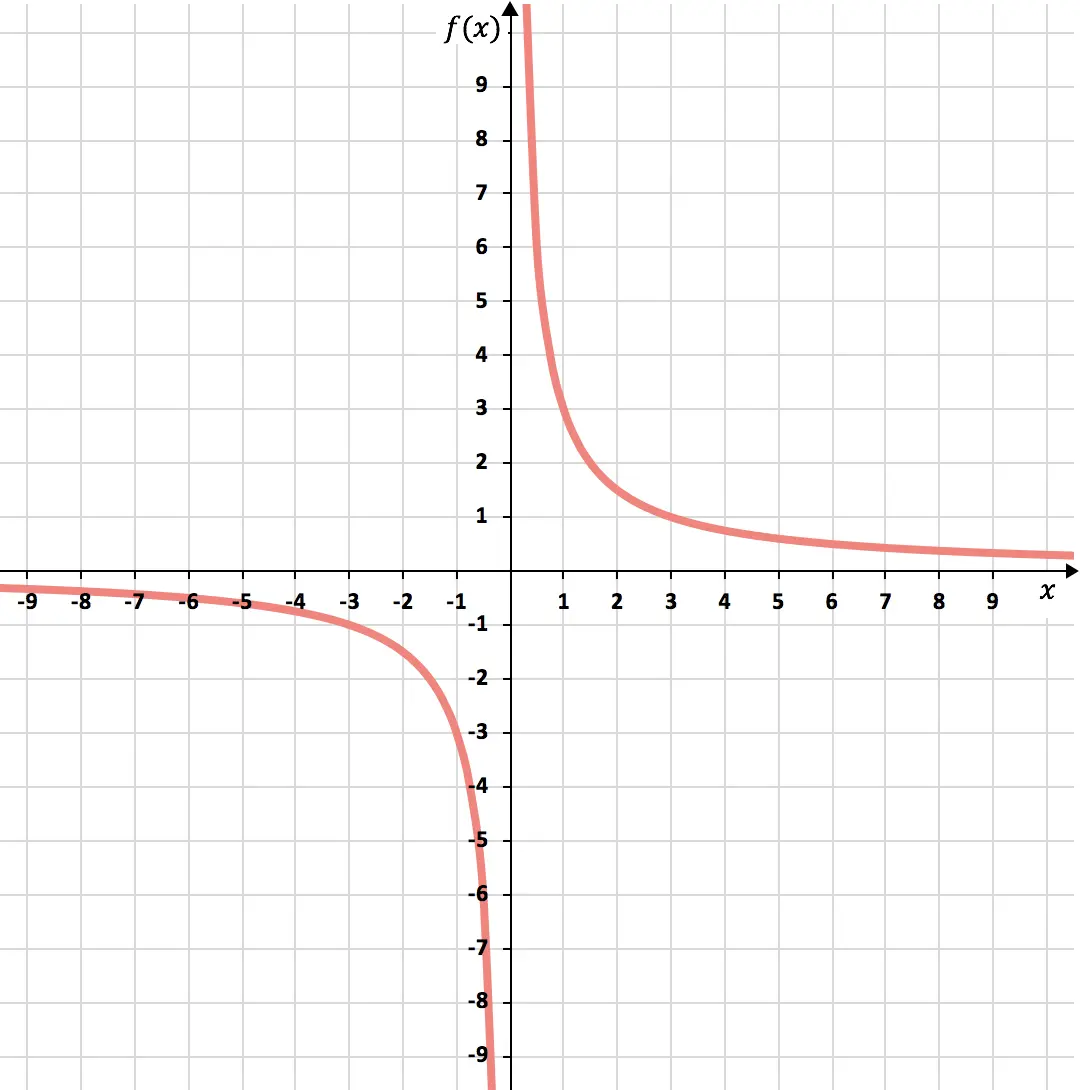
演習 3
次の反比例関数をグラフにします。
![]()
最初に行うことは、関数の定義域を計算することです。
![]()
![]()
![]()
関数のドメインがわかったら、値のテーブルを作成します。

最後に、得られた点をグラフ上に表し、双曲線をプロットして、反比例関数を形成します。
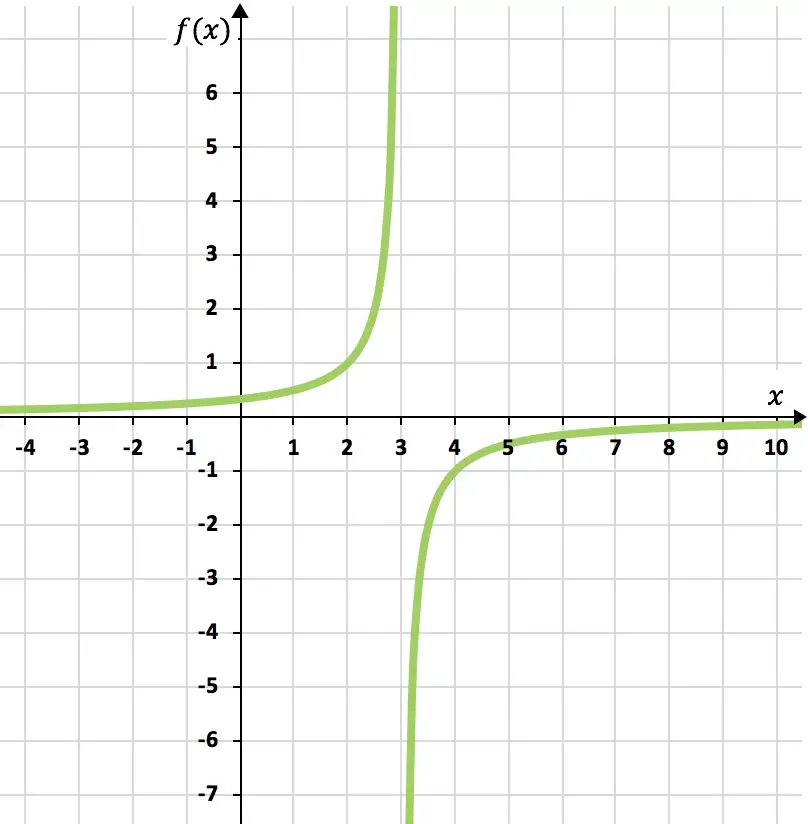
演習 4
次の反比例関数をグラフにします。
![]()
まず、関数の定義域を計算する必要があります。
![]()
![]()
![]()
![]()
関数のドメインがわかったら、値の配列を作成します。
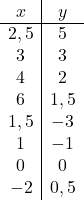
そして最後に、得られた点をグラフ上に表して双曲線を描き、反比例関数を形成します。
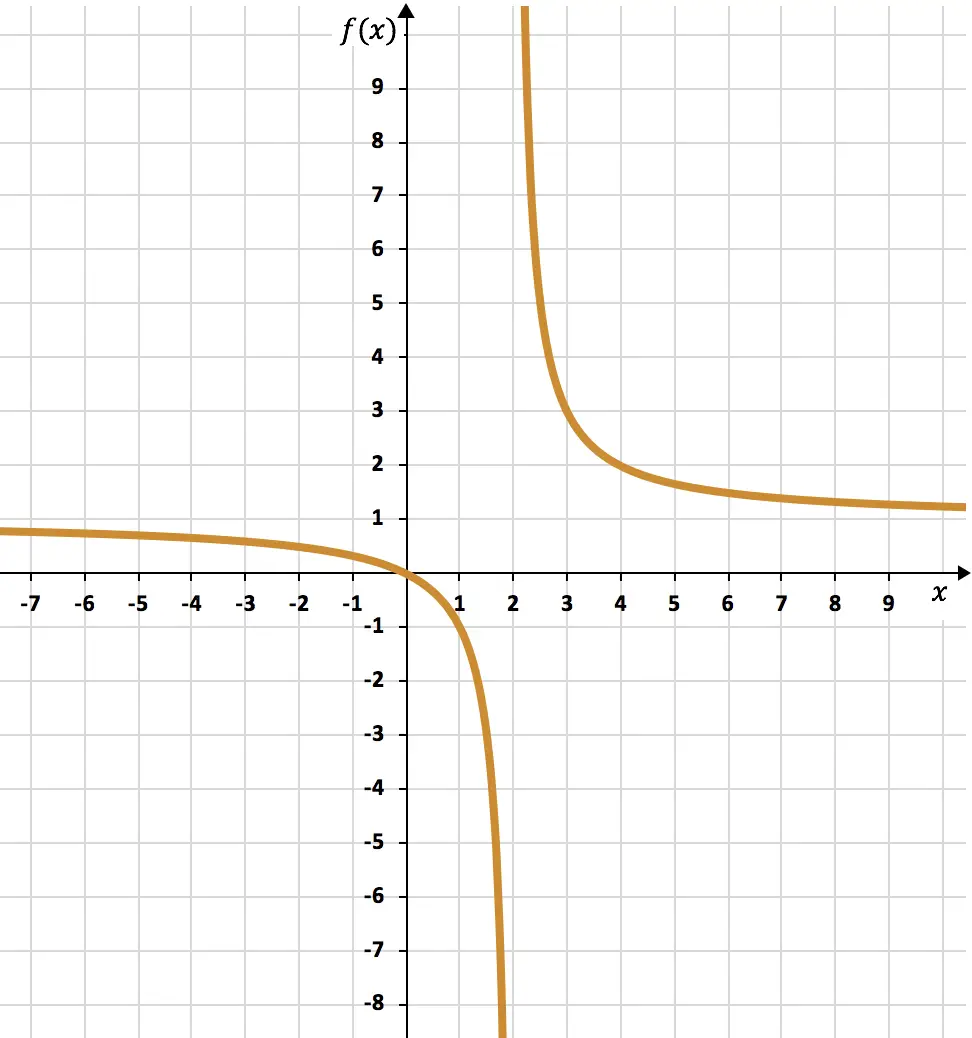
演習 5
次の有理関数をグラフにします。
![]()
最初に行うことは、関数の定義域を計算することです。
![]()
![]()
![]()
![]()
関数のドメインがわかったら、値のテーブルを作成します。

最後に、得られた点をグラフ上に表して双曲線を描くだけで、分数関数が形成されます。

反比例関数の応用
反比例関数は物理学や数学でよく登場します。
たとえば、一定の温度 k にさらされた理想気体の圧力と体積の関係を記述するために使用されます。この関数はボイル・マリオットの法則 (P×V=k) と呼ばれ、反比例関数の一例です。明らかに、負の体積や圧力がないため、この関数の定義領域は正の分岐にのみ限定されます。
一定の電位差の影響を受ける電流強度と電気抵抗の間の関係も、反比例関数によって支配されます。この関数はオームの法則 (V=I×R) として知られています。