この記事では、2つの関数の積(公式)を求める方法を説明します。さらに、関数の積の導関数の例をいくつか確認したり、乗算の導関数に関する解決済み演習を使って練習したりすることもできます。
積の導関数の公式
2 つの異なる関数の積の導関数は、最初の関数の導関数と 2 番目の未微分関数の積と、最初の未微分関数と 2 番目の関数の導関数の積とに等しくなります。
言い換えると、 f(x)とg(x)が 2 つの異なる関数である場合、2 つの関数間の乗算の導関数の式は次のようになります。
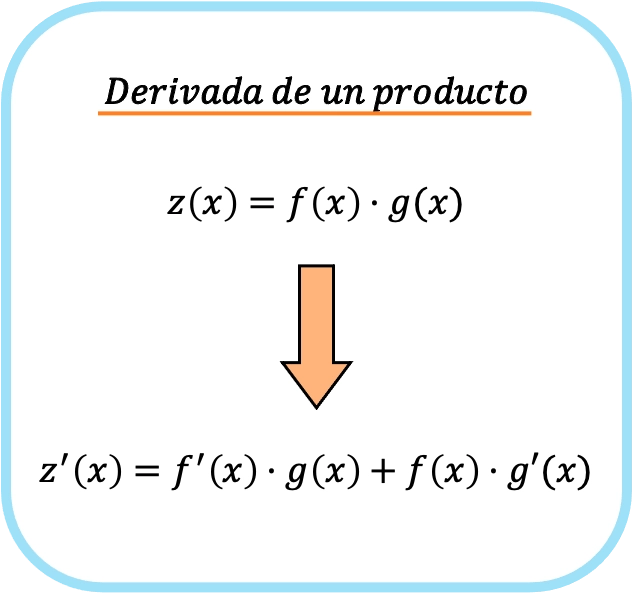
したがって、積の微分規則を適用すると、単純な乗算から 2 つの異なる積が得られます。
製品の派生製品の例
積(または乗算)の導関数の公式が何であるかを理解したら、このタイプの導関数のいくつかの例を解きます。これにより、2 つの関数の積がどのように導出されるのかを理解しやすくなります。
例1
この例では、次の乗算によって 2 つのポテンシャル関数の導関数を解きます。
![]()
前のセクションで見たように、乗算の導関数の公式は次のとおりです。
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-775fe6e5ac196e5a44c840866e35062d_l3.png)
したがって、最初に各関数の導関数を個別に計算する必要があります。
![]()
![]()
各関数の導関数がわかれば、2 つの関数の積の導関数の公式を適用できます。つまり、最初の因子の導関数を微分せずに 2 番目の因子で乗算し、次に 2 番目の因子の微分で微分せずに最初の因子の積を加算します。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=5x^2\cdot (x^3+4x-6)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00f424cf1f72c1d3822c14d49873253e_l3.png)
最後に、得られた結果を単純化するための操作を実行します。
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)& =10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\\[1.5ex] & = 10x^4+40x^2-60x +15x^4+20x^2 \\[1.5ex] & = 25x^4+60x^2-60x\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-48b8d455b68b87932ca3a437f5ffe3a3_l3.png)
例 2
この場合、関数によって定数の積を導き出します。
![]()
積の導関数ルールは次のとおりです。
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-775fe6e5ac196e5a44c840866e35062d_l3.png)
したがって、製品の一部である各関数を個別に導出します。
![]()
![]()
次に、乗算の導関数にルールを適用します。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=7\cdot (x^2+3x)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=0\cdot (x^2+3x)+7\cdot (2x+3)=14x+21\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c2d81edaa002aeb66ca6eec22bec001_l3.png)
定数の導関数は常にゼロであることに注意してください。そのため、定数に関数を乗算した導関数は、定数と関数の導関数の積に等しいと推測できます。
![]()
例 3
指数関数と自然対数の積を解いてみましょう。
![]()
2 つの関数の乗算の導関数の公式は次のとおりです。
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-775fe6e5ac196e5a44c840866e35062d_l3.png)
したがって、最初に積を形成する各関数の導関数を個別に作成する必要があります。これは次のとおりです。
![]()
![]()
したがって、関数の派生積は次のようになります。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=4^{3x}\cdot \ln(x^2)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=4^{3x}\cdot \ln (4) \cdot 3\cdot \ln(x^2) +4^{3x}\cdot \cfrac{2}{x} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e1cb417a69252fe05883f7963bcb8db_l3.png)
製品の派生製品に関する演習を解決しました
次の関数積を派生します。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{B) }f'(x)&=8x\cdot (6x^3-7)+(4x^2+1)\cdot 18x^2\\[1.2ex]&=48x^4-56x+72x^4+18x^2\\[1.2ex]&=120x^4+18x^2-56x \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f46e303cda3be6c3781f7ee4c46c1680_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{F) }f'(x)=& 4\left(10x^6-6x^5\right)^3\cdot (60x^5-30x^4)\cdot \text{arcsen}(x^2+9x)\ +\\[1.2ex] &+\left(10x^6-6x^5\right)^4\cdot \cfrac{2x+9}{\sqrt{1-\left(x^2+9x\right)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5dbaa6f333ff27c717b6478d26154025_l3.png)
3つの機能を備えた製品から派生
次に、3 つの関数の乗算の導関数の公式を残しておきます。これは、2 つの関数の乗算の導関数と非常に似ており、場合によっては役立つためです。
3 つの関数の積の導関数は、最初の関数と他の 2 つの関数の導関数の積、2 番目の関数と他の 2 つの関数の導関数の積、および次の関数の導関数の積に等しくなります。 3 番目の関数.他の 2 つの関数による関数。
![]()
たとえば、次の 3 つの異なる関数の乗算を導出したい場合:
![]()
導関数を解くには、3 つの関数の積の導関数の規則を適用する必要があります。したがって、次のようになります。
![]()
積の導関数の式のデモンストレーション
最後に、乗算の導関数の公式を示します。暗記する必要はありませんが、公式がどこから来たのかを理解しておくことは常に良いことです。 🙂
導関数の数学的定義から:
![]()
関数zを 2 つの異なる関数の積とします。
![]()
定義によれば、 zの導関数は次のようになります。
![]()
![]()
ご存知のとおり、加算と減算によって項を追加しても、両方が同じ項である限り、結果には影響しません。したがって、次のステップに進むことができます。
![]()
ここで、境界プロパティを使用して、前の境界を 2 つの異なる境界に分離します。
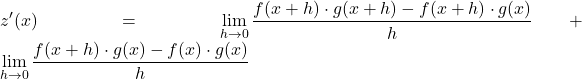
2 つの分数の分子の共通因数を抽出します。
![]()
一方で、次の制限の結果がわかっています。
![]()
したがって、制限を単純化できます。
![]()
![]()
最後に、残りの 2 つの制限に注目すると、それぞれが関数の導関数の定義に対応しています。したがって、平等は次のように単純化できます。
![]()
または同等のもの:
![]()