二項式 - マソリティ

このページでは、二項式とは何かについての説明があり、さらに、各タイプの二項式の例を見ることができます。また、二項を使った演算を解くために使用される公式も示します。二項の乗算、二項の二乗、二項の三乗などです。

ペアとは何ですか?

代数における二項式の定義は次のとおりです。

二項式は、2 つの単項式のみで構成される多項式です。言い換えれば、二項式は、プラス記号 (+) またはマイナス記号 (-) で結合された 2 つの異なる項のみを含む代数式で構成されます。

二項という言葉はギリシャ語に由来しており、2 つの語彙要素 ( biとnomos ) で構成されており、次の意味を持ちます。

bi : 意味2の接頭語。
nomos : 部分という意味です。

したがって、二項式、つまり 2 つの部分 (または 2 つの単項式) を持つ多項式の意味を推測できます。

一方、ペアの概念には数学的な意味とは別の意味があります。つまり、ペアは、政治生活、特定のスポーツ分野、さらにはエンターテイメントにおいて主導的な役割を持つ 2 人の人格のセットを指定することもできます。。しかし、明らかに、ここでは二項式の数学的定義に焦点を当てます。

二項式の例

二項式の概念を理解するために、このタイプの多項式の例をいくつか見ていきます。

二次二項式の例:

$x^2+4x$

3 次二項の例:

$x^3+5$

4次二項の例:

$3x^4+8x^2$

二項式が何であるかがわかったので、さまざまな種類の二項式があり、二項式を使用した演算がどのように解決されるかを見ていきます。

二項二乗

二乗二項式は顕著な恒等性であり、顕著な積または顕著な等価性とも呼ばれます。二項式の 2 乗を解く方法は、それが和二項式であるか差二項式であるかによって異なります。

和二項式とは、2 つの項が正である二項式を指します。つまり、二乗和二項式は次のようになります。

$(a+b)^2$

一方、差分 (または減算) 二項式は加算二項式の共役です。つまり、その単項式の 1 つが負の符号を持ちます。したがって、二乗二項差の代数式は次のようになります。

$(a-b)^2$

2 乗二項を計算するには、これまで見てきたように、加算か減算かによって異なる式を適用する必要があります。 注目すべき等式の公式でこれがどのように行われるかを調べてください。ここでは、ステップバイステップの説明、例、およびこれら 2 つの注目すべき等式だけでなく、すべての演習を確認できます。

二項三乗

あまり使用されませんが、キューブ二項式も注目すべき製品とみなされます。言い換えれば、二項式の立方体を素早く見つけることを可能にする数学的規則が存在します (それらは、注目すべき恒等式の上のリンクで見ることができます)。

前と同様、この強化の結果は、それが合計の 3 乗であるかどうかによって異なります。

$(a+b)^3$

あるいは、逆に、累乗が差または減算の 3 乗で構成される場合は、次のようになります。

$(a-b)^3$

論理的には、2 乗二項式と 3 乗二項式の主な違いはべき指数です。ただし、3 乗二項式の式は、2 乗二項式の式よりもはるかに複雑です。

注目すべき合意

特に、あまり知られていない注目すべきアイデンティティ (または注目すべき製品) に対応するため、その特性により少し特殊な特定のタイプの二項式が存在します。

平方和：
$a^2+b^2$
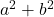
二乗の差 (または減算):
$a^2-b^2$
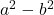
立方体の和:
$a^3+b^3$
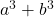
立方体の差 (または減算):
$a^3-b^3$

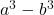
金

$a$

そして

$b$

は任意の 2 つの単項式です。

これらの二項式は、上で見たもの (二項二乗と二項三乗) によく似ていますが、よく見ると異なります。この意味で、上のリンク「⬆ 注目すべき恒等式の公式」をクリックすると、注目すべき二項式の公式とその演繹を確認することもできます。⬆

二項乗算

二項式を使用した最も一般的な演算の 1 つは乗算です。次に、二項間の乗算を計算する方法の例を見ていきます。

$(x^2+2x)\cdot (x-5)$

二項乗算を計算するには、まず最初の二項式の各項を 2 番目の二項式の各項で乗算する必要があります。

$x^2\cdot x+x^2\cdot (-5)+2x\cdot x +2x\cdot (-5)$

$x^3-5x^2+2x^2 -10x$

次に、類似した用語、つまり同じリテラル部分を持つ用語をグループ化します。

$\bm{x^3-3x^2 -10x}$

このようにして、ペア間の積の結果を見つけることができました。

共通項を持つ 2 つの二項式の積

乗算に関与する二項式が共通項として変数を持つ場合

$x,$

この二項演算をすばやく計算する公式があります。

$(x+a)(x+b) = x^2+(a+b)x+ab$

ここでは、この公式を適用する方法を確認できるように、解決済みの演習を示します。

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

ニュートンの二項式

ニュートンの二項は二項定理とも呼ばれ、二項のべき乗を計算するために使用される公式です。

ニュートンの二項式の数学式は次のとおりです。

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}x^{n-k}y^k$

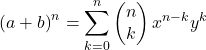
または同等のもの:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

ご覧のとおり、この式は理解するのが少し複雑です。これが、よりよく理解できるように、最も低い次数の二項式のべき乗を以下に示した理由です。

上で見たように、もっと単純な式があるため、この式は 2 乗または 3 乗の二項式を計算する場合には少し面倒になる可能性があります。ただし、ニュートンの二項式は、より高次のべき乗を見つけるのに非常に役立ちます。たとえば、4 次までの二項式を決定するために広く使用されています。

ただし、この公式を適用するには、組み合わせ数、つまり次の型の代数式を計算する方法を知っている必要があります。

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$

、計算は簡単ではありません。 🔍このため、右上の検索エンジンでこれがどのように行われるかを検索することをお勧めします🔎 を参照すると、この操作を段階的に説明した記事が見つかります。