このページでは、行列が特異であるか縮退していることが何を意味するのかを説明します。さらに、疑問を抱かないよういくつかの例を示し、最後にこのタイプのマトリックスのすべてのプロパティを説明します。
特異行列または縮退行列とは何ですか?
特異行列 (縮退行列とも呼ばれます) の定義は次のとおりです。
特異行列または縮退行列は反転できない正方行列であるため、行列式は 0 に等しくなります。
したがって、行列が特異であるかどうかを知るには、行列式を計算するだけです。結果が 0 の場合、行列は特異です。一方、行列式が 0 と異なる場合、行列は特異ではありません。 。
逆行列についてさらに詳しく知りたい場合は、ガウス法を使用して行列を逆行列にする方法が詳細に説明されているこのページを参照してください。また、練習のために段階的に解決されるいくつかの例と演習も見つかります。
一方、特異行列は、 正則行列の正反対の意味を持つため、非正則行列とも呼ばれます。
特異行列の例
特異行列または縮退行列の説明を理解したら、いくつかの次元を持つ特異行列の例をいくつか見てみましょう。
2×2 特異行列の例
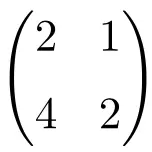
行列式を計算することで、それが特異行列であることを簡単に検証できます。
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 2&1 \\[1.1ex] 4 & 2\end{vmatrix}\bm{=0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e8466c3a7108986306c5e06a6b49049_l3.png)
次数 2 の行列の行列式は 0 に等しいため、特異行列です。
3 × 3 特異行列の例
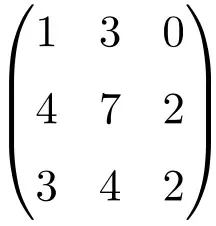
行列の行列式を解いて、それが非可逆行列であることを確認する必要があります。
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1&3&0\\[1.1ex] 4&7&2\\[1.1ex] 3&4&2\end{vmatrix}\bm{=0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1aebdc318be6773a6d4d78e9fcedaf5d_l3.png)
次数 3 の行列の行列式は 0 を与えるため、特異行列になります。
4 × 4 特異行列の例
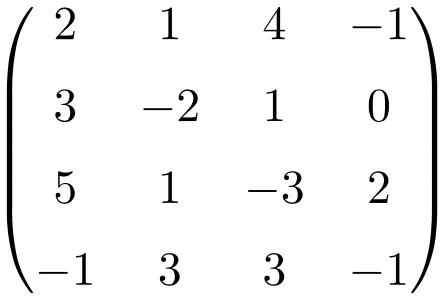
行列の行列式を作成することで、それが特異行列であることを示します。
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 2&1&4&-1\\[1.1ex] 3&-2&1&0\\[1.1ex] 5&1&-3&2\\[1.1ex] -1&3&3&-1\end{vmatrix}\bm{=0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ad6c7444321a65bb993c2abc87f93a0_l3.png)
次数 4 の行列の行列式は 0 であるため、その逆行列は存在しません。
警告:行列式の計算に疑問がある場合は、行列式の計算方法のページを参照してください。
特異行列のプロパティ
このタイプの行列の特徴は次のとおりです。
- 特異行列の少なくとも 2 つの列または 2 つの行は線形結合であり、線形従属です。
- ゼロで埋められた行または列を含む行列は、特異行列です。
- 特異行列または縮退行列のランクは、そのサイズよりも小さくなります。
- 特異行列に他の行列を乗算すると、別の特異行列が得られます。この条件は、行列式の特性から推定できます。
![]()
- 同様に、特異行列の累乗は、累乗された累乗に関係なく、別の特異行列と等しくなります。
- 転置された (または転置された) 行列の行列式は非転置行列の行列式と同等であるため、特異行列の転置により別の特異行列が生じます。
![]()
- 特異行列にスカラーを乗算しても、縮退行列としてのステータスは変わりません。
- 特異行列の随伴項も特異です。
- 三角行列と対角行列は、主対角要素の少なくとも 1 つがゼロの場合、縮退行列になります。
- 明らかに、ゼロ行列は特異行列です。
- 同様に、零ポテント行列も特異行列です。
- 特異行列に関連付けられた線形方程式系には解がないか、無限に多くの解があります。
- 最後に、正方行列は、0 に等しい固有値 (または固有値) を少なくとも 1 つ持つ場合にのみ特異です。