ここでは、差の 2 乗 (または減算) の注目すべき恒等公式が何であるかを説明します。つまり、式 (ab) 2がどのように解かれるかを示します。さらに、例を見て、差の二乗で解く練習問題を練習することができます。最後に、この注目すべき製品タイプの公式のデモンストレーションと幾何学的解釈を示します。
差(または減算)の二乗は何ですか?
差の 2 乗、または減算の 2 乗は、 注目すべき恒等式(または注目すべき積) の 1 つです。つまり、これは、「2 つの項: 1 つの正の項を持つ二項式」の求積法の計算を容易にする数学的規則で構成されています。そしてもう一つは否定的です。
したがって、差の二乗の代数式は(ab) 2です。
差の二乗(または減算)の公式
このタイプの注目すべきアイデンティティの定義を理解したら、その公式を使用して差の 2 乗を解く方法がわかります。

したがって、差の 2 乗は、最初の項の 2 乗から、最初の項と 2 番目の項の積の 2 倍を引いたものに、2 番目の項の 2 乗を加えたものと等しくなります。
したがって、差または二乗減算を計算するには、各項を 2 にするだけでなく、それらを一緒に 2 で乗算する必要があります。
これは覚えておくことが重要です。なぜなら、二乗を減算するときに非常によくある間違いは、2 つの項の間に積を入れず、減少の二乗と減算の減算だけを解くことだからです。

aとbの間の積を忘れないでください。
差(または減算)二乗の例
差の二乗の公式がわかったので、それを使って計算を行うことができます。これがどのように行われるかを理解できるように、差の 2 乗 (または減算) の解決例をいくつか用意しました。
例1
- 次の差の二乗を解きます。
![]()
これは二乗減算なので、次の式を適用する必要があります。
![]()
したがって、未知の値が何であるかを特定する必要があります
![]()
そして
![]()
式の。この場合、
![]()
変数です
![]()
そして
![]()
番号 3 に対応します。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1bb2d14a30d2cdabae6458f5df32392a_l3.png)
負号は含まれないことに注意してください。
![]()
ただし、数式を正しく適用するには、常に符号なしの数値を使用する必要があります。
したがって、私たちはすでに次の値を知っています
![]()
そしての
![]()
したがって、これらの値を式に代入するだけで済みます。

例 2
- 次の二乗減算の二項を計算します。
![]()
二乗差の公式は次のとおりです。
![]()
したがって、最初に次の値を特定する必要があります。
![]()
そしての
![]()
式の。この問題では、
![]()
単項式を表します
![]()
そして
![]()
は二項式の独立項、つまり 2 に相当します。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (5x-2)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=5x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-868a41eb665f5bc94959448547c060d5_l3.png)
最後に、パラメーターの値がわかったら、
![]()
そして
![]()
、単純に二乗減算の二項式を適用します。
![Rendered by QuickLaTeX.com \begin{aligned} (5x-2)^2 & = (5x)^2-2\cdot 5x \cdot 2 + 2^2 \\[2ex] & = 25x^2-20x+4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5e88231a654b23a306e53e17d175d25_l3.png)
差の二乗の公式の証明
次に、減算の二乗の公式がどこから来たのかを推測します。証明を暗記する必要はありませんが、その背後にある数学を理解することは依然として良いことです。
すべての減算の二項式から始めると、次のようになります。
![]()
明らかに、前の累乗は係数の積に等しい
![]()
それ自体を乗算します:
![]()
次に、分配プロパティを適用して 2 つの括弧を乗算します。
![Rendered by QuickLaTeX.com \begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b46073fd758d93fff8956f0a8dd57af_l3.png)
そして、式の証明を完了するには、類似した用語をグループ化するだけです。
![]()
減算の二乗の公式を数学的に証明するには、次のようにします。
![]()
興味深いことに、二乗減算の二項式の拡張は完全二乗三項式としても知られています。
差の二乗の幾何学的解釈
差の二乗の概念を理解するために、この驚くべき等価性を幾何学的に解釈する方法を見ていきます。
次の辺が長さの正方形を見てください。
![]()
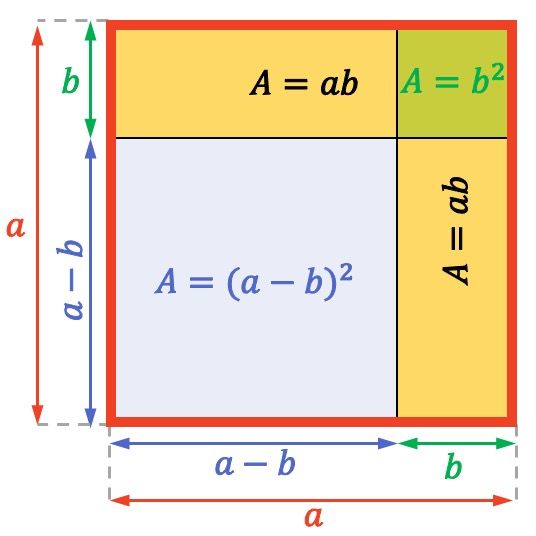
正方形または長方形の面積 (または表面積) は、隣接する 2 つの辺を乗算して計算されます。したがって、上の整数平方全体の面積は、
![]()
同様に、各黄色の長方形の面積は次のようになります。
![]()
最後に、右上に示されている小さな正方形の面積は、
![]()
これは、辺の正方形を意味します
![]()
その表面は
![]()
次元の正方形の領域に分解できます
![]()
寸法の長方形の面積のマイナス2倍
![]()
そして
![]()
、一辺の正方形の面積を加えたもの
![]()
つまり、差の二乗の公式は幾何学的にも検証できます。
![]()
差の二乗(または引き算)の問題を解決しました
練習できるように、注目すべき差の 2 乗積について段階的に解決するいくつかの演習を用意しました。ご質問がございましたら、以下のコメント欄にご記入ください。
演習 1
次の減算の二乗を解きます。
![]()
![]()
![]()
![]()
![]()
問題の顕著な正体をすべて見つけるには、次のような差の 2 乗の公式を適用するだけで十分です。
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14d502eda968fe82617b4403cd9c4722_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c22d520301280872e645f5683a2fba8e_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95c7c481a96b20b700bd2253c90f0c0d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cea9fa89580d3d9d9df7fd93cca2b89_l3.png)
![Rendered by QuickLaTeX.com \text{E)} \ \begin{aligned}(4x-3y)^2 & = (4x)^2-2\cdot 4x\cdot 3y +(3y)^2\\[2ex] & = \bm{16x^2-24xy+9y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-138b359ce2e8f8b1012c6ecf1b7fb9b0_l3.png)
演習 2
次の式を適用して、2 つの量の差の 2 乗を求めます。
![]()
![]()
![]()
問題の注目すべき積をすべて決定するには、二乗減算の公式を使用する必要があります。
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2\\[2ex] & = \bm{36x^6-48x^3y^4+16y^8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c73b9ba584f955a0cae5564a2226d465_l3.png)
セクション B) を解決するには、ルートが 2 乗されると単純化されることを覚えておく必要があります。
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-38cd9e9855f7f79f607247ccc731e297_l3.png)
最後の二乗減算の単項式には分数係数があるため、これを解くには分数の性質を使用する必要があります。
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2 & = \left(\frac{5}{2}x^2\right)^2-2\cdot \frac{5}{2}x^2\cdot \frac{4}{5}x +\left(\frac{4}{5}x\right)^2\\[2ex] & = \frac{5^2}{2^2}x^4-2\cdot \frac{20}{10}x^3 +\frac{4^2}{5^2}x^2 \\[2ex] &= \frac{25}{4}x^4 -2\cdot 2x^3+\frac{16}{25}x^2 \\[2ex] & = \mathbf{\frac{25}{4}} \bm{x^4-4x^3+}\mathbf{\frac{16}{25}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-46106420913cc7a370e2f5215af0f2a2_l3.png)