このページでは、アイデンティティ (またはユニット) マトリックスとは何かと、いくつかの例を示します。さらに、単位行列の特性、このタイプの行列の操作方法、行列式の結果についても説明します。最後に、この非常に特殊なマトリックスが持つ応用例を示します。
単位行列とは何ですか?
ID (または単位) 行列は、主対角を除き、すべての要素が 1 (1) であるゼロ (0) で満たされた正方行列です。
これは恒等行列または統一行列の定義ですが、例を通してより明確に理解できるでしょう。
恒等行列の例
2×2次元の単位行列の例
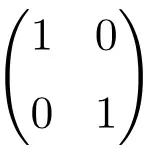
3×3 次の恒等行列の例

サイズ 4×4 の恒等行列の例
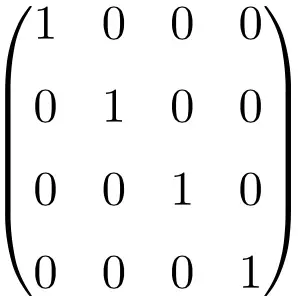
ご覧のとおり、単位行列を構築するには、同じ手順に従う必要があります。主対角に 1 (1) を置き、残りはすべて 0 (0) です。変わるのはテーブルのサイズだけです。
識別テーブルのプロパティ
単位行列、単位行列、または同一行列さえも数学で広く使用されています。これは、このタイプの行列が持つ次の特性によるものです。
- 単位行列は対角行列の一例です。
- ユニタリ行列は、上三角行列と下三角行列の両方です。
- 単位行列も対称行列です。
- 単位行列の代理はそれ自体です。
![Rendered by QuickLaTeX.com \displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-16454b80729e9e2059e118dfc5ba2f8a_l3.png)
- 可逆行列です。そして、随伴については、単位行列の逆行列自体は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e9ca14cfbc1b230347abb6e36464e9c_l3.png)
- 任意のスカラー行列は、数値と単位行列の乗算から取得できます。
![Rendered by QuickLaTeX.com \displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ba48a8806ab085937939bada831e91e_l3.png)
- 同一行列のすべての固有値 (または固有値)は 1 です。
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b9a461140ed125bbcc26d551b255cdc_l3.png)
- 最後に、単位行列も置換行列の例です。
ID (または単位) マトリックスを使用した操作
あなたはおそらく次のように考えているでしょう: これはすべて非常に良いことですが…、アイデンティティ マトリックスは何のためにあるのでしょうか?それが 0 と 1 を含むテーブルだったらよかったのに。
まだこのトピックを取り上げていないかもしれませんが、単位行列は数学でよく使用されます。実際、このタイプの正方行列は線形代数では非常に重要です。単位行列の主な有用性は、行列演算の計算が容易になることです。それでは、恒等行列を操作する方法を見てみましょう。
恒等行列を使った加算と減算
他の要素を変更せずに行列の主対角に数値を加算 (または減算) する 1 つの方法は単位行列を使用することです。単位行列はそれらの数値に 1 単位のみを加算 (または減算) するためです。要素:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4a357b8c79a1f4f70a5dcdeadcbe3e46_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2f549edd3cac0340615dae86bf7e2932_l3.png)
最初に単位行列にスカラーを乗算することで、対角要素にさらに単位を加算または減算することもできます。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-85520cb04e8697d315a6e5002c8e1dea_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a90c8c3b8f9635561f6c85e7b003734c_l3.png)
行列と単位行列の乗算
行列に単位行列を乗算すると、行列は中立要素として機能します。つまり、行列に単位行列を乗算すると、結果は同じ行列になります。次の例を見てください。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-345f47fb447c1877462d8c9358f8eb89_l3.png)
さらに、行列の積の意味は無関係です。つまり、結果は常に同じ行列になるため、単位行列に右を乗算するか左を乗算するかは問題ではありません。これを実証するために、前の演習を繰り返しますが、今回は恒等行列に反対側を乗算します。
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b9a6c50074dc2594054453a6b53f4862_l3.png)
単位行列の力
行列を累乗する指数や行列の次元に関係なく、単位行列の累乗は常に単位行列になります。
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e8dbc082f20a9a9b5b5c9b1b443833c4_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-67a36555e36ab97ce2c663bf32c8e97d_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2efa9dcf6ec3b986aaff19701a794899_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14cad3370ec38fd0ed7ebb3a5fa96282_l3.png)
単位行列の行列式
すでに想像していると思いますが、Identity (または Unit) 行列の行列式は、行列の次元に関係なく、常に 1 に等しくなります。
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-718871901f1660f8f5202ea312c39584_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5971cf3c43e11184380d55d43f69ba8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4efd00fdafcbe456d1b5060344fe8d5_l3.png)
恒等行列アプリケーション
最後に、ここまでの情報をすべて読んだ後、単位行列がなぜそれほど重要なのかという典型的な質問への答え方はおそらくすでにご存知でしょう。リラックスしてください、私も以前にこの質問を自分自身に問いかけました。 😂
お気づきのとおり、恒等行列には多くの用途があり、それが非常に興味深い理由です。ユニット行列の用途の 1 つは演算です。これまで見てきたように、ユニット行列を使用して行列演算を実行するのは非常に簡単です。
一方、単位行列は行列方程式を解くためにも使用されます。これを行うには、次の逆行列プロパティを使用します。行列とその逆行列の乗算は単位行列に等しいです。リンクをクリックすると、行列を使用して方程式を解く方法を確認できます。
さらに、単位行列は、ガウス法による逆行列の計算にも使用されます。この方法では、単位行列の隣に行列を配置して、より大きな行列を形成します。次に、行に基本演算を適用して、元の行列を単位行列に変換する必要があります。非常に複雑に見えますが、実際はそれほど複雑ではありません。ただし、手順全体を適用する必要があるため、より興味がある場合は、Web ページの検索エンジンで行列を反転する方法を検索してください (上から右へ)。
最後に、恒等行列は、行列を対角化し、その固有値 (または固有値) を計算するのにも役立ちます。単位行列が介入する特定の演算によって、固有値を取得するための特性多項式を取得できるためです。しかし、それはすでに非常に高度な主題であるため、行列の対角化に特化した超包括的なページ全体を用意し、例とそれを説明する解決済みの演習を用意しています。さらに興味がある場合は、検索エンジン (右上) でこのガイドを検索してください。