このページでは、3×3 正方行列の行列式が何であるかを学びます。 Sarrus ルールを使用して次数 3 の行列式を解く方法がわかります。さらに、例題と練習問題が段階的に解決されているので、実践して完全に理解することができます。
3×3行列の行列式は何ですか?
次数 3 の行列式は、行列の各辺の垂直バーで表される 3 × 3 次元の行列です。たとえば、次の行列があるとします。
![\displaystyle A = \begin{pmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b5e89b706893e88dd15882e3685afb1_l3.png "Rendered by QuickLaTeX.com")
行列 A の行列式は次のように表されます。
![\displaystyle \lvert A \rvert = \begin{vmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41db04327de87a80f1e0e4dd6dcb220a_l3.png "Rendered by QuickLaTeX.com")
これまで見てきたように、次数 3 の正方行列の行列式を書くのは簡単です。では、それを解決する方法を見てみましょう。
次数 3 の行列式を計算するにはどうすればよいですか?
3×3 行列の行列式を作成するには、 Sarrus の規則を適用する必要があります。
サラスルール
Sarrus のルールによれば、次数 3 の行列式を計算するには、主対角要素の積と、その平行対角線と対応する反対側の頂点の積を加算し、次に副対角要素の積を減算し、それらの平行な対角線と、対応する反対側の頂点との積。
このように書くと少しわかりにくいかもしれませんが、次の図と例で 3×3 の行列式の計算がどのように行われるかを見てください。
3×3 行列式の例:
![\begin{aligned} \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} & = 2 \cdot 1 \cdot 1 + 1 \cdot 0 \cdot (-2) + (-1) \cdot 4 \cdot 3 - (-2) \cdot 1 \cdot 3 - 4 \cdot 0 \cdot 2- (-1) \cdot 1 \cdot 1 \\ & = 2 + 0 -12 +6 - 0 +1 \\[2ex] & = \bm{-3} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-98e60cf465cd0eb7662d47770cd38231_l3.png "Rendered by QuickLaTeX.com")
![\begin{aligned} \begin{vmatrix} 1 & 0 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 4 & -3 & -1 \end{vmatrix} & = 1\cdot 2 \cdot (-1) + 0 \cdot 1 \cdot 4 +3 \cdot (-3) \cdot 2 - 4 \cdot 2 \cdot 2 - (-3) \cdot 1 \cdot 1- 3 \cdot 0 \cdot (-1) \\ & = -2 +0 -18 - 16 +3- 0 \\[2ex] & = \bm{-33} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41a53c1fd6eae1b51a280a6ce1e2ab91_l3.png "Rendered by QuickLaTeX.com")
3 × 3 行列の行列式の問題を解決しました
演習 1
次の 3×3 行列式を解きます。
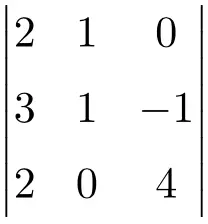
3×3 行列の行列式を解くには、Sarrus の法則を適用する必要があります。
![\displaystyle\begin{aligned} \begin{vmatrix} 2 & 1 & 0 \\[1.1ex] 3 & 1 & -1 \\[1.1ex] 2 & 0 & 4 \end{vmatrix} & = 2 \cdot 1 \cdot 4 + 1 \cdot (-1) \cdot 2 + 3 \cdot 0 \cdot 0 - 2 \cdot 1 \cdot 0 - 0 \cdot (-1) \cdot 2- 3 \cdot 1 \cdot 4 \\ & = 8 -2 +0 -0- 0-12 \\[2ex] & = \bm{-6} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f288312b72f3bbabc35ee64bf580d8c_l3.png "Rendered by QuickLaTeX.com")
演習 2
次の次数 3 の行列式を計算します。
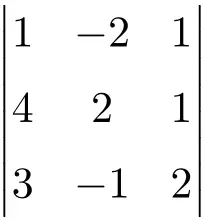
3 次行列の行列式を計算するには、Sarrus の法則を使用する必要があります。
![\displaystyle\begin{aligned} \begin{vmatrix} 1 & -2 & 1 \\[1.1ex] 4 & 2 & 1 \\[1.1ex] 3 & -1 & 2 \end{vmatrix} & = 1 \cdot 2 \cdot 2 + (-2) \cdot 1 \cdot 3 + 4 \cdot (-1) \cdot 1 - 3 \cdot 2 \cdot 1 - (-1) \cdot 1 \cdot 1 - 4 \cdot (-2) \cdot 2 \\ & = 4 -6 -4 -6+1+16 \\[2ex] & = \bm{5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-64078968233ec50d2e793309d55e55fc_l3.png "Rendered by QuickLaTeX.com")
演習 3
次の 3×3 行列の行列式の解を求めます。
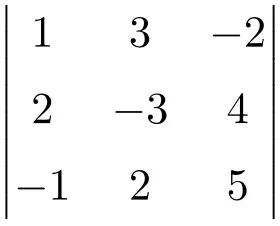
3×3 行列の行列式を作成するには、Sarrus の法則を使用する必要があります。
![\displaystyle\begin{aligned} \begin{vmatrix}1 & 3 & -2 \\[1.1ex] 2 & -3 & 4 \\[1.1ex] -1 & 2 & 5 \end{vmatrix} & = \\ & = 1 \cdot (-3) \cdot 5 + 3 \cdot 4 \cdot (-1) + 2 \cdot 2 \cdot (-2) \ - \\[1.1ex] & \phantom{=} - (-1) \cdot (-3) \cdot (-2) - 2 \cdot 4 \cdot 1 - 2 \cdot 3 \cdot 5 \\[2.5ex] & = -15 -12 -8 +6-8-30 \\[2.5ex] & = \bm{-67} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd4494ae66a604834b8f9f47fcbbe41d_l3.png "Rendered by QuickLaTeX.com")
演習 4
次の 3 次行列の行列式の解を求めます。
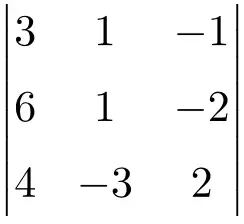
3×3 行列の行列式の解を求めるには、Sarrus の公式を適用する必要があります。
![\displaystyle\begin{aligned} \begin{vmatrix} 3 & 1 & -1 \\[1.1ex] 6 & 1 & -2 \\[1.1ex] 4 & -3 & 2 \end{vmatrix} & = \\ & = 3 \cdot 1 \cdot 2 + 1 \cdot (-2) \cdot 4 + 6 \cdot (-3) \cdot (-1) \ - \\[1.1ex] & \phantom{=} - 4 \cdot 1 \cdot (-1) - (-3) \cdot (-2) \cdot 3 - 6 \cdot 1 \cdot 2 \\[2.5ex] & =6 -8 +18 +4-18-12 \\[2.5ex] & = \bm{-10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e811024d460a60a1df59983b1f700e8_l3.png "Rendered by QuickLaTeX.com")
演習 5
の値を見つけます
これにより、次の 3 次行列式がキャンセルされます。
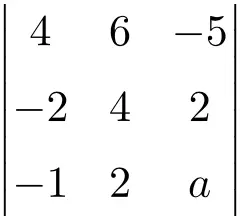
まず、Sarrus の法則を使用して、行列式の値を次の関数として計算します。
![\displaystyle\begin{aligned}\begin{vmatrix} 4 & 6 & -5 \\[1.1ex] -2 & 4 & 2 \\[1.1ex] -1 & 2 & a \end{vmatrix} & = \\ & = 4 \cdot 4 \cdot a + 6 \cdot 2 \cdot (-1) + (-2) \cdot 2 \cdot (-5) \ - \\[1.1ex] & \phantom{=}- (-1) \cdot 4 \cdot (-5) - 2 \cdot 2 \cdot 4 - (-2) \cdot 6 \cdot a \\[2.5ex] & = 16a -12 + 20 - 20 - 16 +12a \\[2.5ex] & = 28a -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-07e67cfc5e45c0a11c35d643cd4c1c78_l3.png "Rendered by QuickLaTeX.com")
行列式が消えるには、結果が 0 でなければなりません。したがって、結果を 0 に設定し、方程式を解きます。
