このページでは多項式の減算方法を説明します。さらに、多項式を減算するためのいくつかの例と段階的な演習も見つかります。
多項式を減算するにはどうすればよいですか?
2 つの多項式を減算するには、類似する多項式の項を減算する必要があります。つまり、多項式の減算は、同じリテラル部分 (同じ変数と同じ指数) を持つ項を減算することで構成されます。
数学では、垂直法と水平法という 2 つの異なる方法で多項式の減算を計算できます。以下に両方の手順の説明を示しますが、まず垂直方向に多項式を減算する方法を学習してから、水平方向の方法に進むことをお勧めします。明らかに、好みのものを使用してください。
垂直多項式の減算
次に、例を使用して 2 つの多項式がどのように垂直方向に減算されるかを見ていきます。
- 引き算をする
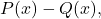
は 2 つの多項式です。
![]()
![]()
多項式の減算を見つけるために最初に行う必要があるのは、1 つの多項式をもう 1 つの多項式の下に配置して、2 つの多項式の同様の項が列に並ぶようにすることです。
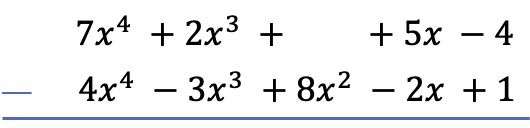
警告:多項式に特定の次数の項がない場合、スペースは空のままにしておく必要があります。たとえば、多項式
![]()
には 2 次単項式がないため、その場所には空のスペースが存在します。
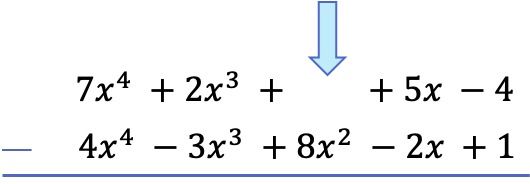
多項式を直接減算できるようになりましたが、この方法で行うと符号を間違えやすくなります。したがって、多項式を減算するには、減算多項式 (減算多項式) のすべての項の符号を変更してから加算を行うのが最善です。多項式を減算することは、その逆の多項式を加算することと同じであるためです。
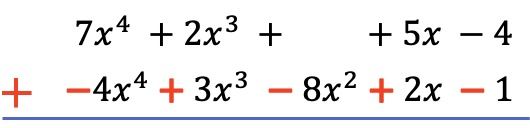
そして、すべての項を最高次数から最低次数の順に並べて、以下の多項式の項を否定したら、リテラル部分を等しく保ちながら各列の係数を追加します。
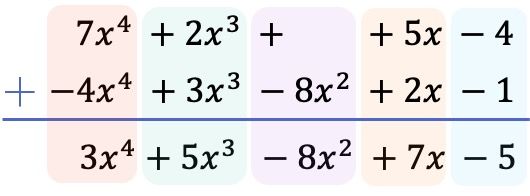
したがって、2 つの多項式の減算から得られる結果は次のようになります。
![]()
最後のステップがよくわからない場合のために、 多項式の加算がどのように行われるかについて説明しておきます。実際、多項式をうまく減算できるようにするには、多項式の加算をマスターすることが不可欠です。リンクされたページには、多項式の加算の例と解答済みの演習もあり、さらに、多項式の加算と減算の違いを確認することもできます。
水平多項式の減算
多項式を垂直方向に減算する方法を説明しましたが、ここでは多項式を減算するためのもう 1 つの方法、つまり多項式を水平方向に減算する方法について説明します。この手順は前の手順より確実に高速ですが、多項式の概念を十分に理解する必要があります。
それでは、例を通して多項式を減算するこの方法がどのようなものであるかを見てみましょう。 2 つの方法の違いがわかるように、前の例と同じ多項式を減算します。
- 余りを計算する
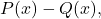
は 2 つの多項式です。
![]()
![]()
まず 2 つの多項式を代数演算の形式、つまり交互に配置する必要があります。
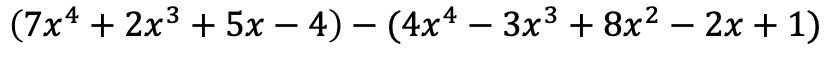
最初の括弧内の単項式は同じままですが、2 番目の括弧内の項は前にマイナスがあるため、符号を変更する必要があります。
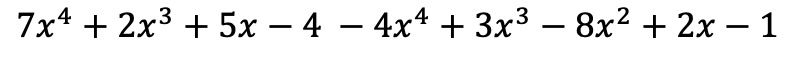
そして今度は、同一のリテラル部分を持つ用語、つまり同じ変数 (文字) と指数を持つ用語をグループ化します。類似していない用語を加算または減算することはできません。
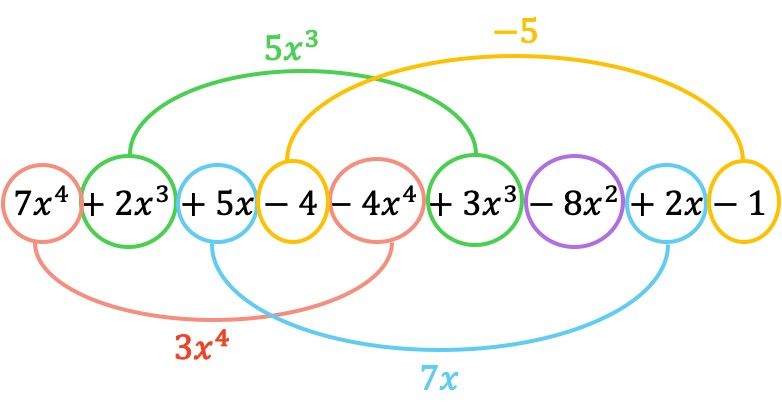
したがって、減算の結果得られる多項式は次のようになります。
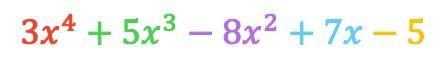
ご覧のとおり、どちらの方法でも同じ結果が得られたため、最適な方を使用してください。
多項式の引き算を解く 2 つの方法を見てきましたが、多項式を使用して分数の引き算もできることをご存知ですか?引き算だけでなく、あらゆる種類の演算も可能です。このリンクをクリックして、 代数分数の演算がどのように行われるかを確認してください。
多項式の減算の問題を解決しました
練習できるように、解決済みの多項式減算の演習をいくつか用意しておきます。エクササイズに関するご質問がございましたら、ページのコメント欄にご記入いただければ、できるだけ早くお答えいたします。
演習 1
多項式の減算
![]()
多項式を引いたもの
![]()
![]()
![]()
この場合、2 つの多項式を垂直方向に減算します。これを行うには、まず多項式を次数で順序付けし、次に残りの多項式項の符号を変更し、最後に同じ列にある単項式を追加します。
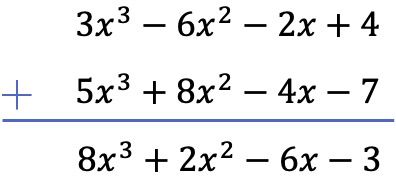
演習 2
減算多項式を解く
![]()
多項式を引いたもの
![]()
![]()
![]()
2 つの多項式を減算すると、減算された多項式の逆を微分多項式に加算することになります。したがって、下請多項式 (残りの 1 つ) の項の符号を変更し、多項式を追加します。
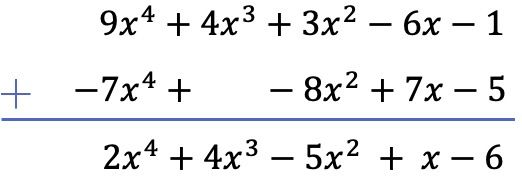
この特定のケースでは、2 番目の多項式の 3 次の列には 3 次の項がないため、空のスペースを残す必要があることに注意してください。
演習 3
多項式を減算した結果を求めます
![]()
多項式を引いたもの
![]()
![]()
![]()
この場合、2 つの多項式の減算を垂直方向に解きます。したがって、最初に多項式を最大次数から最小次数の順に並べ、次に残りの多項式の項の符号を変更し、最後に同様の項を追加します。
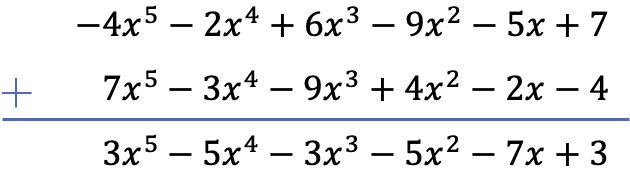
演習 4
多項式を使用して次の演算を計算します。
![]()
![]()
![]()
![]()
この場合、3 つの多項式が演算に関係し、そのうち 2 つは減算です。したがって、この演算を解決するには、残りの 2 つの多項式のすべての項の符号を変更してから、多項式を加算します。
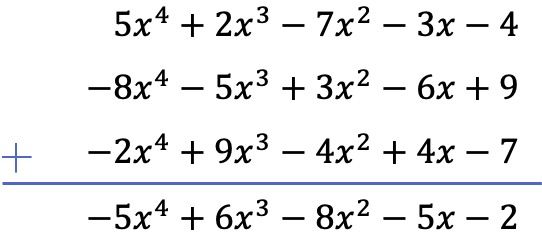
その説明についてどう思いますか?役に立ちましたか?多項式を減算する場合、垂直方向と水平方向のどちらの方法が好みですか?コメントを読んでいます! 👀