このページでは、数値と行列を乗算する方法を説明します。また、完全に理解するのに役立つ例と、練習できるように解決された演習も用意されています。スカラーと行列の積のプロパティもすべて見つかります。
数値に行列を掛けるにはどうすればよいでしょうか?
数値と行列を乗算するには、行列の各要素に数値を乗算します。
例:

数値と行列の乗算に関する問題を解決しました
演習 1:
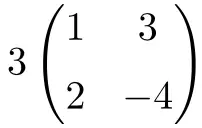
これは、スカラーと次数 2 の正方行列の乗算です。
![Rendered by QuickLaTeX.com \displaystyle 3 \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -4 \end{pmatrix} = \begin{pmatrix} 3\cdot 1 & 3\cdot 3 \\[1.1ex] 3\cdot 2 & 3\cdot (-4) \end{pmatrix} = \begin{pmatrix} \bm{3} & \bm{9} \\[1.1ex] \bm{6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-590b79c0fea524b963397181b6f2bea8_l3.png)
演習 2:
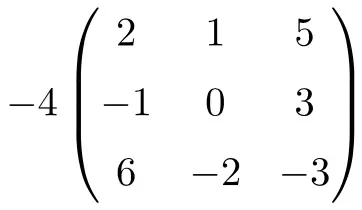
これは、数値と次数 3 の正方行列の積です。
![Rendered by QuickLaTeX.com \displaystyle -4 \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -1 & 0 & 3 \\[1.1ex] 6 & -2 & -3 \end{pmatrix} = \begin{pmatrix} -4 \cdot 2 & -4 \cdot 1 & -4 \cdot 5 \\[1.1ex] -4 \cdot (-1) & -4 \cdot 0 & -4 \cdot 3 \\[1.1ex] -4 \cdot 6 & -4 \cdot (-2) & -4 \cdot (-3) \end{pmatrix}= \begin{pmatrix} \bm{-8} & \bm{-4} & \bm{-20} \\[1.1ex] \bm{4} & \bm{0} & \bm {-12} \\[1.1ex] \bm{-24} & \bm{8} & \bm {12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5042f0f8cd9b7a4d0e28974f793b145b_l3.png)
演習 3:
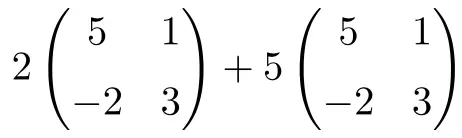
これは、数値と行列の積と 2×2 次元の行列の和を組み合わせる演算です。
![Rendered by QuickLaTeX.com \displaystyle 2 \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}+5\begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56d2a40f021be13a5d92d0c10d353684_l3.png)
したがって、最初に製品について次のことを解決する必要があります。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 10 & 2 \\[1.1ex] -4 & 6 \end{pmatrix}+\begin{pmatrix} 25 & 5 \\[1.1ex] -10 & 15 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-068901abef987767025bb01b24579226_l3.png)
そして最後に、結果の行列を追加します。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{35} & \bm{7} \\[1.1ex] \bm{-14} & \bm{21} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d15ea16036f522af0f23fee0bb796757_l3.png)
演習 4:
次の行列を考えてみましょう。
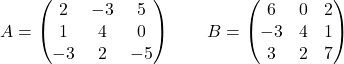
計算します:
![]()
これは、スカラー乗算と 3 × 3 次元の行列の加算および減算を組み合わせた演算です。さらに、マトリックスは、
![]()
は単位行列で、主対角要素の 1 と残りの要素の 0 で構成されます。
![Rendered by QuickLaTeX.com \displaystyle -2\begin{pmatrix} 2 & -3 & 5 \\[1.1ex] 1 & 4 & 0 \\[1.1ex] -3 & 2 & -5 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} -3 \begin{pmatrix} 6 & 0 & 2 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 3 & 2 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dce934040dc05714321dbbeac4e20c73_l3.png)
したがって、最初に乗算を実行します。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} -4 & 6 & -10 \\[1.1ex] -2 & -8 & 0 \\[1.1ex] 6 & -4 & 10 \end{pmatrix}+\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc26f29384abcfb6f08a36b601e4ff61_l3.png)
最初の 2 つの行列を追加します。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 6 & -10 \\[1.1ex] -2 & -3 & 0 \\[1.1ex] 6 & -4 & 15 \end{pmatrix}-\begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-897ec02d46bc09bdec58d9b3246c6f4d_l3.png)
最後に、行列の減算を実行します。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{-17} & \bm{6} & \bm{-16} \\[1.1ex] \bm{7} & \bm{-15} & \bm{-3} \\[1.1ex] \bm{-3} & \bm{-10} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ddd808a46a137f4c7742545c4f76f46_l3.png)
行列のスカラー積に関するこれらの演習が役に立った場合は、行列の加算と行列の積、さらに繰り返される 2 種類の行列演算について段階的に解決される演習を躊躇せずに練習してください。
数値と行列の積のプロパティ
ご存知のとおり、行列には正方行列、三角行列、単位行列など、さまざまな種類があります。しかし、幸いなことに、数値と行列の積のすべてのプロパティは、すべてのクラスの行列に対して有効です。
スカラーと行列の間の乗算のプロパティは次のとおりです。
- 関連プロパティ:
![]()
次の 2 つの演算を見てください。2 と 3 をどのように乗算しても同じ結果が得られます。
![Rendered by QuickLaTeX.com \displaystyle 2 \cdot \left(3 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} \right) =2 \cdot \begin{pmatrix} 3 & 0 \\[1.1ex] 6 & -3 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b4e9fd568edd5833238d8d21fdf4d1a8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle (2 \cdot 3) \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} =6 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f8ee596b3e2ca16ff1c507717982ee1_l3.png)
- スカラーの加算に関する分配特性:
![]()
以下の例でわかるように、最初に 1+2 を加算してから行列で乗算する場合、または行列に 1 と 2 を個別に乗算して結果を加算する場合は同じです。
![Rendered by QuickLaTeX.com \displaystyle (1 + 2) \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} =3 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-025ac9b0851ed93fd0c3870328d6144b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle 1 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4\end{pmatrix} = \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5\\[1.1ex] -2 & -4 \end{pmatrix} + \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & 10 \\[1.1ex] -4 & -8\end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2f54f4d5ae113e2462b752c150b3f43b_l3.png)
- 行列の加算に関する分配特性:
![]()
つまり、2 つの数学行列を加算して数値を乗算することは、2 つの行列に同じ数値を個別に乗算してその結果を加算することと同じです。以下の例では、次のことを確認できます。
![Rendered by QuickLaTeX.com \displaystyle 4 \cdot \left( \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+\begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} \right) =4 \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 6 & 3 \end{pmatrix}= \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cdb35d5c66ee525c3d52fe7576e75758_l3.png)
![Rendered by QuickLaTeX.com \displaystyle 4 \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+ 4 \cdot \begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} = \begin{pmatrix} 12 & -8 \\[1.1ex] 24 & -4 \end{pmatrix}+\begin{pmatrix} -4 & 12 \\[1.1ex] 0 & 16 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ef9d3f8f503371fa5f3d2478f728d88_l3.png)
- 中立要素のプロパティ:
![]()
したがって、行列に 1 を乗算するときは、行列を変更しません。
![Rendered by QuickLaTeX.com \displaystyle 1 \cdot \begin{pmatrix} 5 & -4 & 0 \\[1.1ex] 1 & 3 & -3 \\[1.1ex] 2 & 9 & 4 \end{pmatrix}=\begin{pmatrix} \bm{5} & \bm{-4} & \bm{0} \\[1.1ex] \bm{1} & \bm{3} & \bm{-3} \\[1.1ex] \bm{2} & \bm{9} & \bm{4} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ee2c0afd1bf2904722701caca883125_l3.png)
これらはすべてスカラーと行列の積のプロパティなので、この記事はこれで終わりです。気に入っていただけたこと、そして何よりも、行列を使った数値の乗算を解く方法を学んでいただけたことを願っています。
一方、乗算に関連する他の行列演算は、非常に便利であり、べき乗です。興味がある方のために、行列とは何か、行列の力を解く方法を学ぶページをここに残しておきます。