このページでは、単項式の各部分 (係数、リテラル部分、次数など) とそれらを簡単に識別する方法について説明します。さらに、例を確認したり、単項式の各部分を段階的に解決する演習で練習したりすることもできます。
単項式の部分は何ですか?
単項式の部分は次のとおりです。
- 係数: 単項式の変数 (または文字) を乗算する数値です。
- 変数: は単項式に現れる各文字です。
- リテラル部分: すべての指数を含む単項式を形成するすべての変数に対応します。
- 次数: 単項変数のすべての指数の合計です。
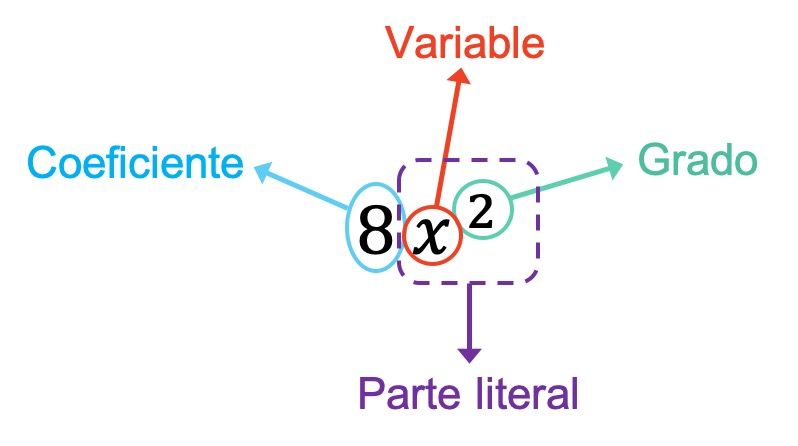
前の例でわかるように、単項式の係数は変数を乗算する数値であるため、8 です。また、この場合、単項式には変数が 1 つだけあり、それが x です。したがって、単項式のリテラル部分は、この変数とその指数、つまり x 2によって形成されます。そして最後に、単項式は指数が 2 だけであるため、2 次になります。
一方、単項式の部分の特性の 1 つは、2 つの単項式が同じリテラル部分を持つ場合、それらは類似した単項式であると言われることです。このタイプの単項式については、リンク先のページで詳しく学ぶことができます。そこでは、とりわけ、単項式が数学にとって非常に重要である理由が説明されています。
単項式の一部の例
単項式の部分の概念を完全に理解できるように、いくつかの例を示します。
例1
![]()
- 単項式の係数:
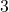
- 単項変数:
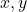
(この場合、変数は 2 つあります)
- 単項式のリテラル部分:
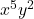
- 単項式の次数:
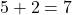
例 2
![]()
- 単項式の係数:
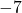
- 単項変数:
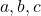
(この場合、変数は 3 つあります)
- 単項式のリテラル部分:
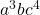
- 単項式の次数:
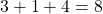
変数の指数が設定されていない場合は、1 に累乗されることを意味するため、実際にはその変数の指数は 0 ではなく 1 になることに注意してください。このため、次の計算に単位を追加しました。この単項式の次数 (3+ 1 +4=8)、
![]()
さらに興味がある場合は、次のリンクで 単項式の例をさらに見ることができます。さらに、存在するさまざまなタイプの単項式、単項式の数値がどのように計算されるか、単項式と多項式の違いについても確認できます。
単項式の一部の問題を解決しました
最後に、単項式の各部分のさまざまな定義を理解していることを確認できるように、いくつかの演習を提供します。
演習 1
次の単項式のすべての部分は何ですか?
![]()
単項式の係数:
![]()
単項変数:
![]()
単項式のリテラル部分:
![]()
単項式の次数:
![]()
演習 2
次の単項式のすべての要素を特定します。
![]()
単項式の係数:
![]()
単項変数:
![]()
単項式のリテラル部分:
![]()
単項式の次数:
![]()
演習 3
次の単項式の部分を分数で求めます。
![]()
単項式の係数:
![]()
単項変数:
![]()
単項式のリテラル部分:
![]()
単項式の次数:
![]()
完璧!ここまで読んだ方は、おそらく単項式の各部分についてすでにすべてを理解しているでしょう。だからこそ、次のレベルに進み、 単項式を使った演算を行う方法を学ぶ準備ができています。ここでは、存在する単項式を使用したすべてのタイプの演算がどのように計算されるかだけでなく、単項式を使用した組み合わせ演算を解く方法もわかり、解決された演習で段階的に練習することができます。