ここでは、線と平面の間の角度がどのように計算されるかを説明します。また、例を見て、さらに、線と平面の間の角度を段階的に解決する演習で練習することもできます。
線と平面の間の角度はいくらですか?
線と平面の間の角度は、線とその平面上の正射影との間の角度です。
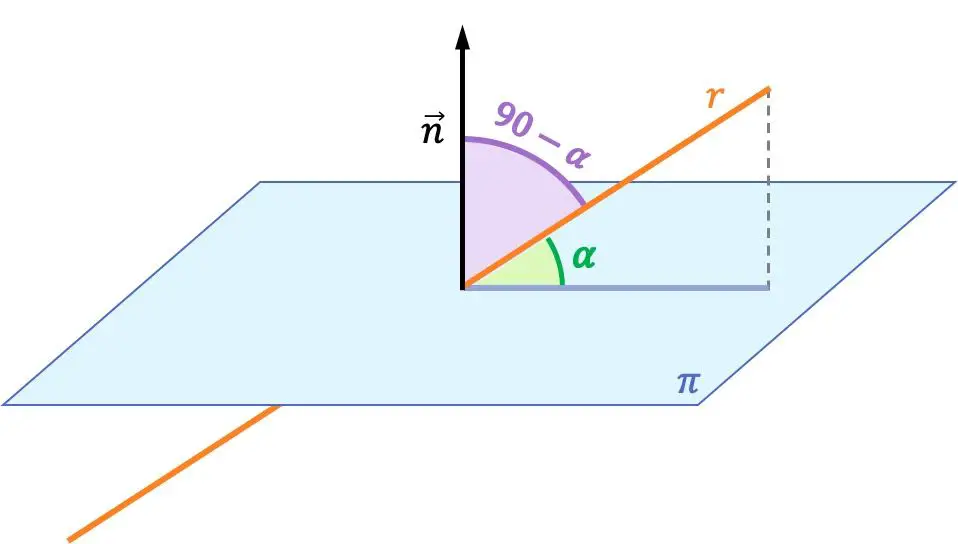
線と平面との間の角度は、前記線とその平面に垂直なベクトルとの間の角度の補数である。したがって、線と面とのなす角度は、線の方向ベクトルと面の法線ベクトルとのなす角度から計算される。
直線と平面の間の角度の公式
平面と直線の間の角度の公式を推定するには、 2 つのベクトルの間の角度を見つける方法を知る必要があります。リンク先のページでは、解説と例題・練習問題をステップバイステップで解いておりますので、やり方を覚えていない方はご覧になることをお勧めします。
したがって、線と平面の間の角度は、その線の方向ベクトルの間の角度と補になるため、
![]()
およびその平面に対する法線ベクトル
![]()
、2 つのベクトル間の角度の公式から、線と平面の間の角度は次の式と同等であると推定されます。
![]()
したがって、線と平面の間の角度の公式は次のようになります。
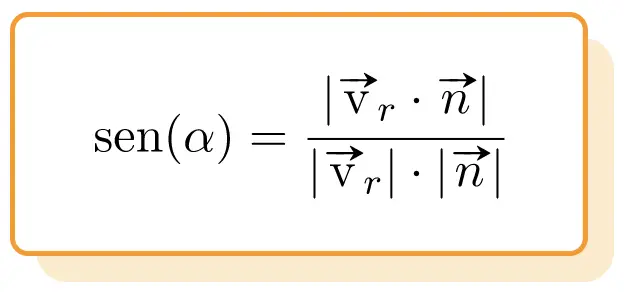
金:
-

は直線の直接ベクトルです。
-
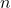
は平面に垂直なベクトルです。
直線と平面の間の角度を計算する例
この種の問題を解決する方法を理解できるように、線と平面の間の角度を計算する例を次に示します。
- 線がなす角度を計算します

飛行機と一緒に
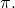
それらの方程式を次のようにします。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-cb8b61cb99a7af826a63ee098efc3a3c_l3.png)
直線はパラメトリック方程式の形式で表現されるため、その方向ベクトルは次のようになります。
![]()
一方、平面は暗黙的な (または一般的な) 方程式の形式で定義されるため、その法線ベクトルは次のようになります。
![]()
したがって、線の方向ベクトルと平面の法線ベクトルがわかったら、線と平面の間の角度の公式を適用します。
![]()
式内のベクトルを次のように置き換えます。
![]()
そして計算を行います。
![]()
![]()
![]()
![]()
最後に、電卓を使用して正弦を反転し、角度の値を求めます。
![]()
したがって、線と平面の間の角度は約 51.80 度になります。
0°の結果が得られた場合、これは線と平面が平行であるか、線が平面に含まれていることを意味することを考慮する必要があります。角度が 90 度に等しい場合、線と平面が垂直であることを意味します。
直線と平面の角度の問題を解決しました
演習 1
線がなす角度を求めます
![]()
飛行機と一緒に
![]()
それらの方程式を次のようにします。
![]()
![]()
直線は連続方程式として表現されるため、その方向ベクトルは次のようになります。
![]()
一方、平面は暗黙的な (または一般的な) 方程式の形式であるため、その法線ベクトルは次のようになります。
![]()
したがって、線の方向ベクトルと平面の法線ベクトルがわかったら、線と平面の間の角度の公式を使用します。
![]()
![]()
![]()
![]()
![]()
![]()
最後に、サインを反転して角度の値を求めます。
![]()
したがって、線と平面の間の角度は 4.10 度になります。
演習 2
線がなす角度を決定する
![]()
飛行機と一緒に
![]()
それらの方程式を次のようにします。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a8165b8e50fbc7764c77d1a984de353_l3.png)
![]()
直線は暗黙的な (または一般的な) 方程式で表現されるため、直線を決定する 2 つの平面に垂直なベクトルのベクトル積を計算して、直線の方向ベクトルを見つける必要があります。
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}](https://mathority.org/wp-content/ql-cache/quicklatex.com-54cc86087728e7e163034c95afc55286_l3.png)
![]()
一方、平面に垂直なベクトルは次のようになります。
![]()
したがって、線の方向ベクトルと平面の法線ベクトルがわかったら、線と平面の間の角度の公式を使用します。
![]()
![]()
![]()
![]()
![]()
最後に、サインを反転して角度の値を求めます。
![]()
したがって、線と平面の間の角度は 46.33 度になります。
演習 3
直線と平面の間の角度の公式を使用して、次の値を求めます。
![]()
権利のために必要な
![]()
そして飛行機
![]()
平行であること。
![]()
![]()
まず、直線はベクトル方程式として表現されるため、その方向ベクトルは次のようになります。
![]()
一方、平面は一般方程式の形式であるため、その法線ベクトルは次のようになります。
![]()
したがって、2 つの幾何学的要素が平行であるためには、それらの間の角度がゼロでなければなりません。したがって、線と平面の間の角度の公式は次のようになります。
![]()
![]()
![]()
![]()
![]()
したがって、線の方向ベクトルと法線ベクトルの内積はゼロでなければなりません。そして、この方程式から未知数の値を決定できます。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
最後に、この記事が役立つと思われた場合は、おそらく2 つの平面間の角度を見つける方法にも興味があるでしょう。リンク ページには、非常に詳細な説明と、2 つの異なる平面間の角度を計算するために必要な公式が記載されています。さらに、実践して理解できるように、段階的に解決される例と演習を見ることができます。それがどのように完璧に行われるのか。